Angles
Solving Quadratics
Graphing Quadratics
Radicals
Special Right Triangles
100
Solve for y
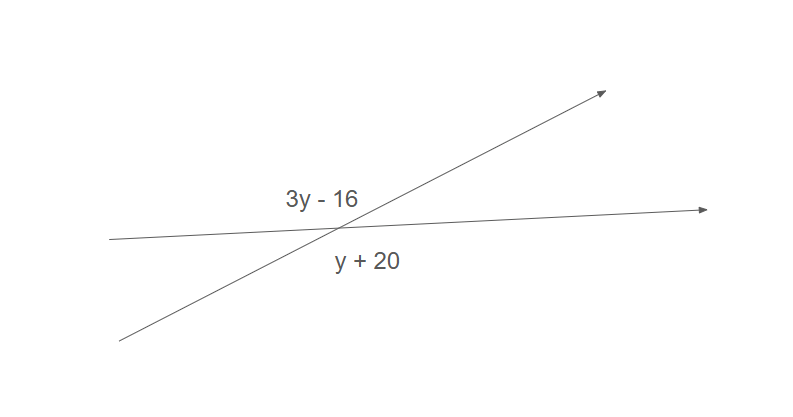
y = 18
100
Solve the quadratic by factoring
0=x^2+10x-24
x = 2 x = -12
100
Find the y-intercept
y = x^2 + 15x - 13
y = -13
100
Simplify
sqrt45
3sqrt5
100
State the missing sides
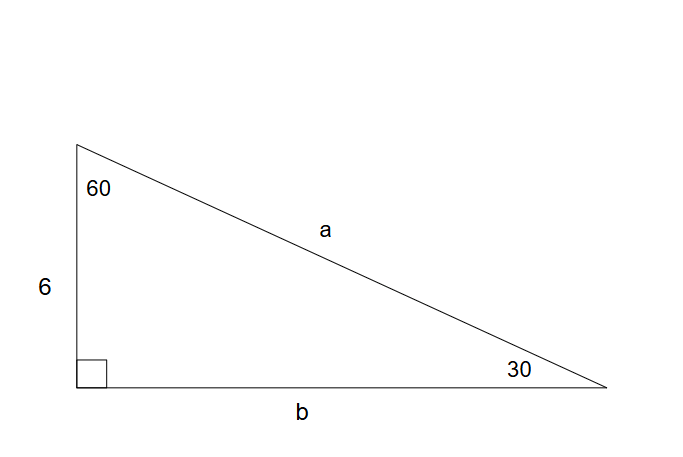
a = 12 b = 6sqrt3
200
Solve for x
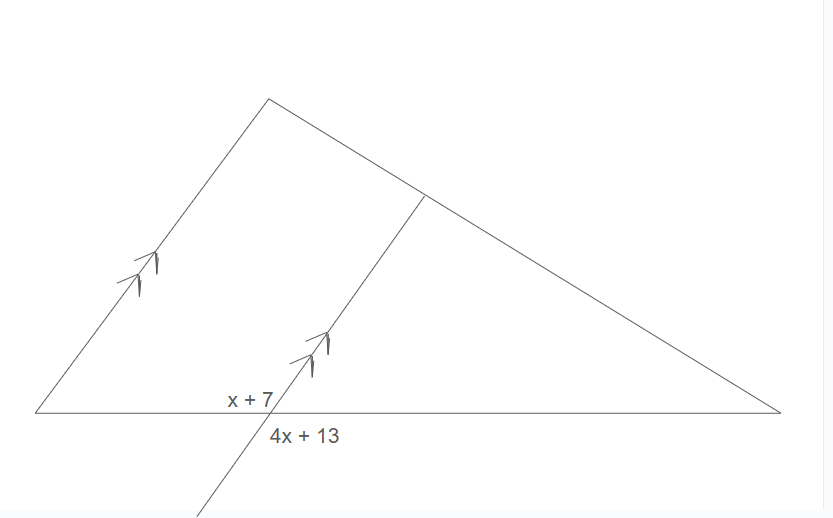
x = -2
200
Solve using the quadratic formula
y=x^2+13x-14
x = 1 x = -14
200
Solve for the x-intercepts
y = (x + 5)(2x - 12)
x = -5 x = 6
200
Add
3sqrt20 + 4sqrt5
10sqrt5
200
Find the missing sides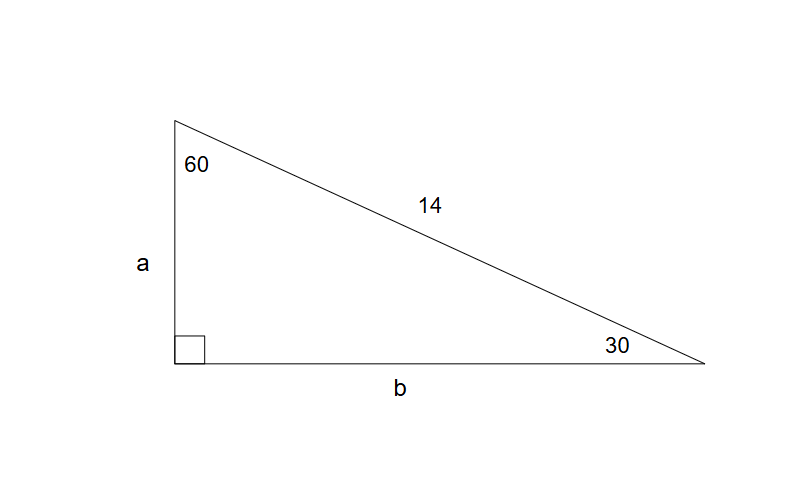
a = 7 b =7sqrt3
300
Solve for x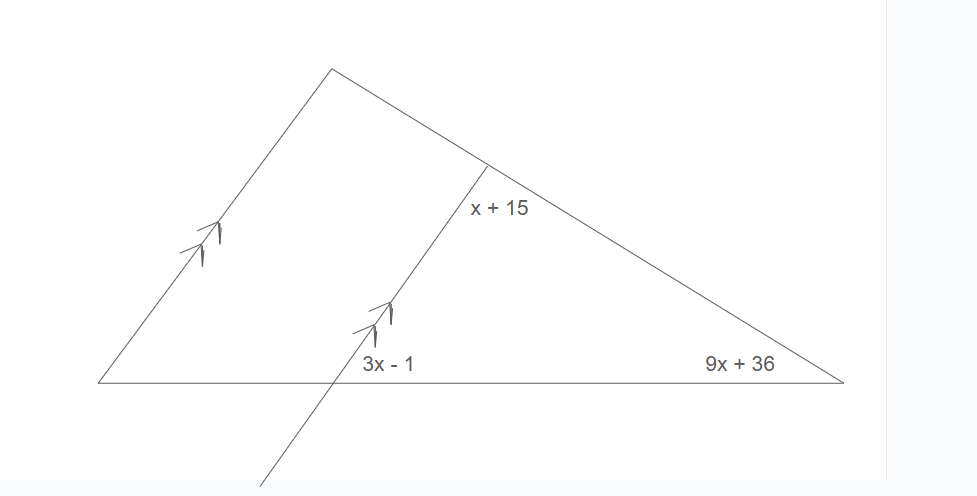
x = 10
300
Solve using the quadratic formula
2x^2-19x-10=0
x=10 x=-1/2
300
Find the vertex by using the formula for the x-value, then plugging in to find corresponding y-value
x=-b/(2a
y = x^2+4x+10
(-2, 6)
300
Multiply
sqrt3(2sqrt5+sqrt6)
2sqrt15+3sqrt2
300
Fill in the missing sides
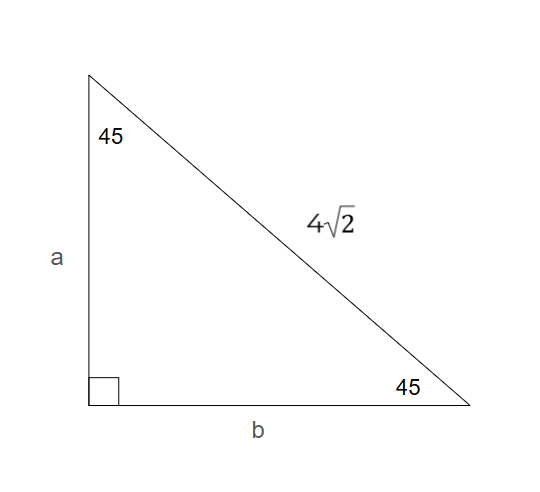
a = 4 b = 4
400
Solve for x and y
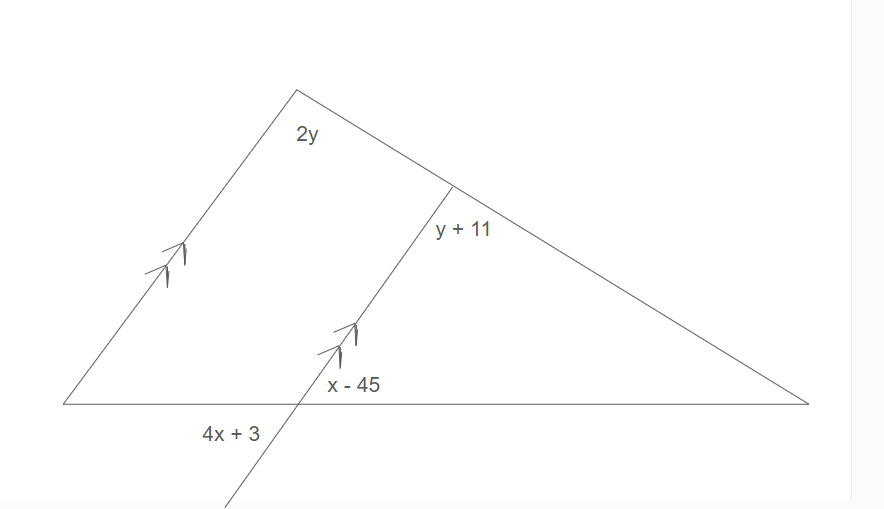
y = 11 x = -16
400
Solve by completing the square
x^2-9x-36=0
x=12 x=-3
400
Convert to Vertex Form by completing the square and state the vertex
y = x^2+8x+14
y = (x+4)^2-2
Vertex: (-4, -2)
400
Multiply
(5+sqrt10)(2+sqrt5)
10+5sqrt5+2sqrt10+5sqrt2
400
Find the perimeter of the triangle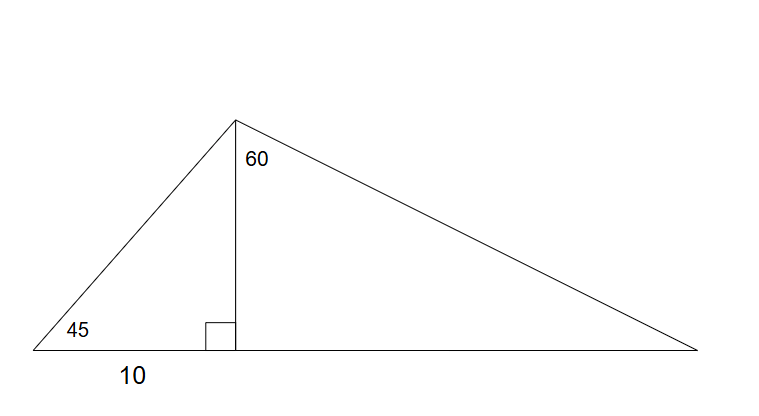
30 + 10sqrt2+10sqrt3
500
Solve for x, y, and z
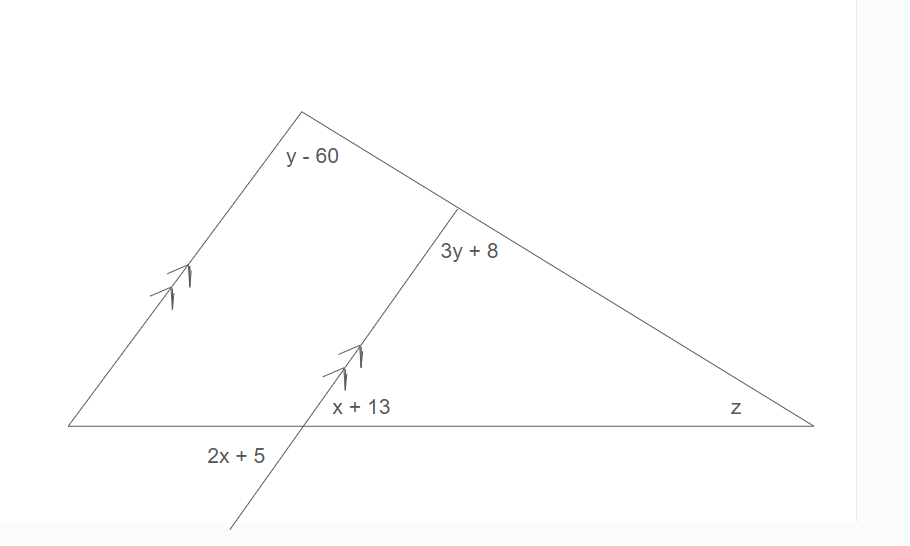
x = 8 y = -34 z = 253
500
Solve using the quadratic formula. Leave in exact form. Simplify all radicals.
2x^2+8x-5=0
x=(-4pmsqrt26)/2
500
Solve for the x-intercepts by using quadratic formula
** Must simplify all answers
y = 3x^2+4x-7
x = 1 x = -7/3
500
Multiply
(7+sqrt5)(2+sqrt5)
19+9sqrt5
500
Find the area of the triangle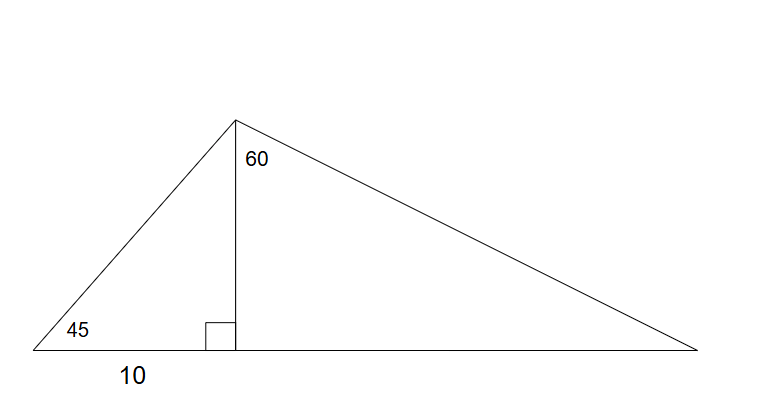
50 + 50sqrt3