What variable will be eliminated?
2x-9y=2
x+9y=5
The y variable will be eliminated
Find the point of intersection.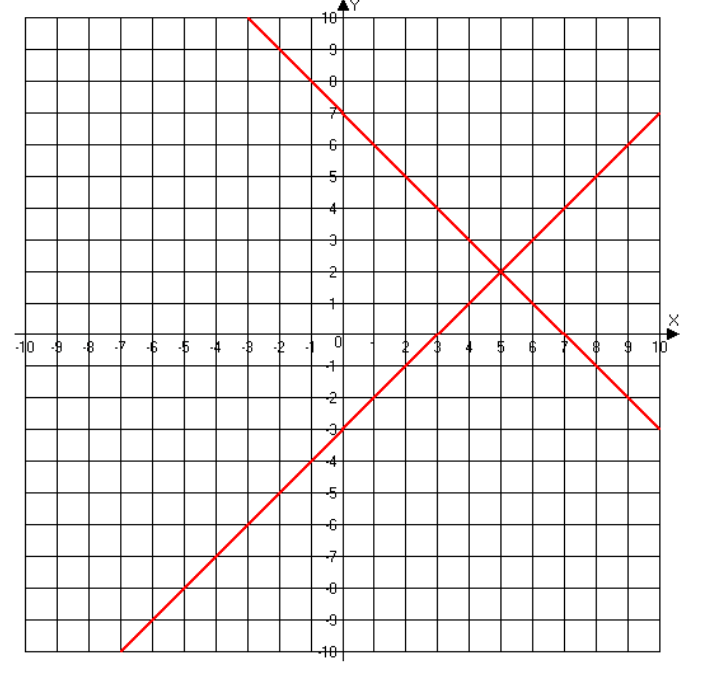
(5,2)
Brooke volunteered at a local community center to raise money for new sports equipment. Brooke worked the food booth where chicken dinners, x, sold for $13 and hamburgers, y, sold for $3. On Saturday night, Brookes booth earned $172 and sold 24 food items. Write a system of equations to represent the situation.
13x+3y=172
x+y=24
Solve the systems of equations using substitution.
x = 5
x + y = 12
(5, 7)
When solving by elimination, what do you look for to know which variable will disappear?
Same Coefficient, Different Signs.
Find the point of intersection.

None, parallel lines
Wyatt volunteered at a local community center to raise money for a new playground. Wyatt worked the food booth where spaghetti dinners, x, were sold for $10 and hamburgers, y, were sold for $2. On Saturday night, Wyatts booth earned $272 and sold 56 items of food. Write a system of equations to represent the situation.
10x+2y=272
x+y=56
Solve the systems of equations using substitution.
y = 2x
x + y = 9
(3, 6)
What must you do to eliminate the x?
2x-3y=9
2x+7y=1
Multiply either equation by a negative 1

(3,-2)
Felicity has 30 pottery pieces for sale in her store. Each vase, v, sells for $21 and each bowl, b, sells for $12.50. If Felicity sells all of her inventory, she will make $477. This situation can be represented by the system of equations shown below.
21v+12.5b=477
v+b=30
How many vases and bowls does Felicity's store have for sale?
12 vases
18 bowls
Solve the systems of equations using substitution.
y=6x-19
y=-2x+5
(3,-1)
What is the solution to the system of equaitons below.
7x+2y=24
-8x-2y=-30
(6,-9)
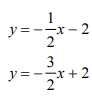
(4,-4)
Martina has 50 cupcakes for sale at her bakery. Each red velvet cupcake, v, sells for $2.75 and each carrot cupcake, c, sells for $3. If Martina sells all of the cupcakes, she will make $142.25. This situation can be represented by the system of equations shown below.
2.75v+3c=142.25
v+c=50
Red Velvet Cupcakes: ________
Carrot Cupcakes:_________
31 red velvet
19 carrot
Solve the systems of equations using substitution.
y = 2x
y - 3x = 8
(-8, -16)
Solve using elimination method
−x + y = 1
−6x + 3y = −12
(5,6)
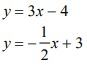
(2,2)
A trail mix is made by adding pecans that sell for $2.50 per pound to chocolate candies that sell for $1.00 per pound. How much of each should be used to get 60 pounds of trail mix that sells for $1.70 per pound?
Pecans: ___________
Chocolate: _________
28 Pecase
32 Chocolate
Solve the systems of equations using substitution.
2x-3y=-24
x+6y=18
(-6,4)