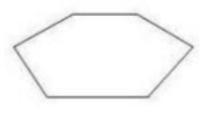
If it is a polygon name it by:
the number of sides,
regular or irregular,
concave or convex.
Hexagon, irregular/unknown, convex
A ________ is a closed plane figure formed by three or more segments that intersect only at their endpoints.
polygon
A parallelogram is a quadrilateral with both pairs of opposite sides:
parallel and congruent
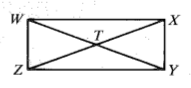
Given: WZYX is a rectangle and WY = 42
Find: XZ
42
The base angles of an isoceles trapezoid are _______.
The legs of an isoceles trapezoid are __________.
Same side interior angles of any trapezoid are ________.
congruent, congruent, supplementary
Find the sum of the interior angles of a heptagon.
900
Find the sum of exterior angles of a dodecagon.
360 for ANY Polygon
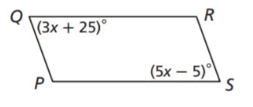
Find the measure of angle S.
70 degrees
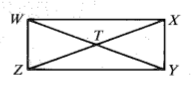
Given: WZYX is a rectangle
/_TXY=50
Find: the measure of angle TYX
50
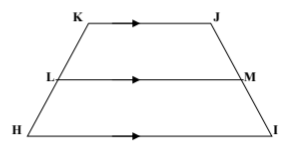
Given: KHIJ is an isosceles trapezoid
KH = 11x +13 and JI = 10x +26
Find KH.
56
Find each angle of a regular octagon.
135
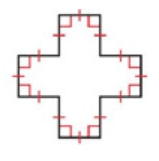
Tell whether the polygon is regular or irregular. Then tell whether it is concave or convex.
irregular, concave
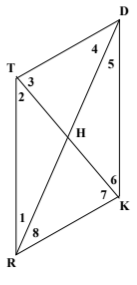
Given: DTRK is a parallelogram
/_2 = 35
Find:
/_6
35
State which parallelograms hold the following property:
Each diagonal is an angle bisector.
Rhombus and Square
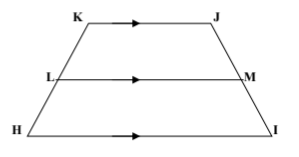
Given: KHIJ is an isosceles trapezoid, LM is a midsegment
KH = 10x + 2 and JM = 2x +10
Find: JI
32
Given that a triangle has exterior angles of 3x, x, and 2x. Find the value of x.
60
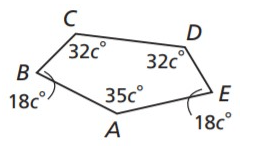
Find the measure of angle E.
72 degrees
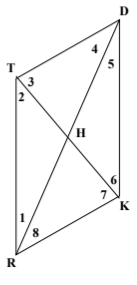
Given: DTRK is a parallelogram
DH = 3x + 5, DR = 7x + 8
Find the distance of HR
11
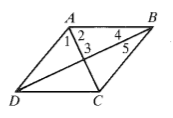
Given: ABCD is a Rhombus
If m∠2 = (3y + 9)° and m∠4 = (2y – 4)°, then y = _____
17
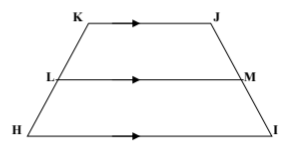
Given: LM is a midsegment
LM = 16, KJ = 2x and HI = 4x+2
Find: x, KJ, and HI
x=5
KJ = 10
HI = 22
Given that a pentagon has exterior angles of:
x, 3x, 2x+4, 7x, and x+6
Find the measure of the largest angle.
175 degrees
The sum of interior angles of a convex polygon is 2340.
Find the number of sides of the polygon.
15

Given: DTRK is a parallelogram
TH = 2x - 3y, TK = 5x - 6y - 2
Find the value of x.
2
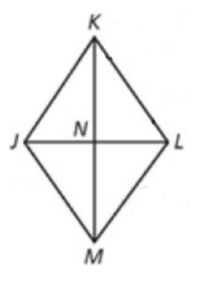
In rhombus JKLM, m∠MNL = (2x + 60)
and m∠LMN = 3x.
Find x. Then find m∠NLM.
x = 15
m∠NLM = 45
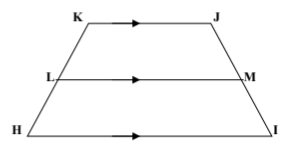
Given: LM is a midsegment
If HI = (4x), LM = (2x + 3),
and KJ = (x - 2)
Find: x, HI, LM, and KJ
x = 8
HI = 32
LM = 19
KJ = 6