Systems of Equations
Distance/Midpoint/Circles
Ellipses
Parabolas
Hyperbolas
100
5y2-x2 = 4
2y = x+3
{(-1, 1), (-29, -13)}
100
Find the distance between the two points and the midpoint: (-3,7), (1,-1)
distance: 4√(5)
midpoint: (-1,3)
100
Give the x and y intercepts of the ellipse x2/9 + y2/4 =1
±3, ±2
100
Find an equation of a parabola with directrix y = 6 and focus (0,2).
y2 = -1/8(x-4)2
100
Graph 25x2-4y2 = 100.
Center: (0,0)
Vertices: (2, 0), (-2, 0)
Asymptotes: y = ±5/2x
200
5x2 -3y2 = 5
x2+3y2 = 91
{(4, 5), (-4, 5), (-4, -5), (4, -5)}
200
Find the distance between the two points and the midpoint: (-a, b), (2a, 4b)
midpoint:
(\frac{a}{2}, \frac{5b}{2})
distance:
3\sqrt{a^2+b^2}
200
Find the length of the major axis, length of the minor axis, center, and foci for the ellipse.
4x2 + y2 -8x + 6y - 23 = 0
ellipse: (x-1)2/9 + (y+3)2/36 = 1
Major axis: 12
Minor axis: 6
Center: (1, -3)
Foci: (1, -3±3√(3))
200
Graph (x-1)2 = -8(y+1). Label the vertex, focus, and directrix.
directrix: y = 1
Vertex: (1, -1)
Focus: (1,-3)
200
Find an equation of the hyperbola having foci (4,0) and (-4,0) and difference of focal radii 6.
x2/9-y2/7 = 1
300
x2+y2=16
x2-y2=20
No solution
300
Find the center and radius of the circle with the equation: x2 +y2+6x-8y-119 = 0
(-3, 4); 12
300
Find an equation of the ellipse with x-intercepts ±5 and y-intercepts ±2√(3).
x2/25 +y2/12 = 1
300
Find the vertex, focus, and directrix of the parabola: y2+8y -12x + 4 = 0
(-1,4), (2,-4), x = -4
300
Find the center, asymptotes, foci, and vertices of the hyperbola: 9x2-16y2-32y+128 = 0
(y+1)2/9 -x2/16 = 1
Center: (0, -1)
Vertices: (0, -4), (0, 2)
Asymptotes: y = ±3/4x -1
Foci: (0,-6), (0, 4)
400
Find an equation of a circle whose diameter has endpoints (0,3) and (4,-3).
(x-2)2 +y2 =13
400
Find an equation of the ellipse with foci (6,2) and (-10, 2) and with 20 as the sum of the focal radii.
(x+2)2/100 + (y-2)2/36 = 1
400
write the equation in standard form, identify the vertex, Axis of symmetry and how it opens.
x=y2-8y-11
x=(y-4)2-27
vertex (-27,4)
AoS y=4 opens right
400
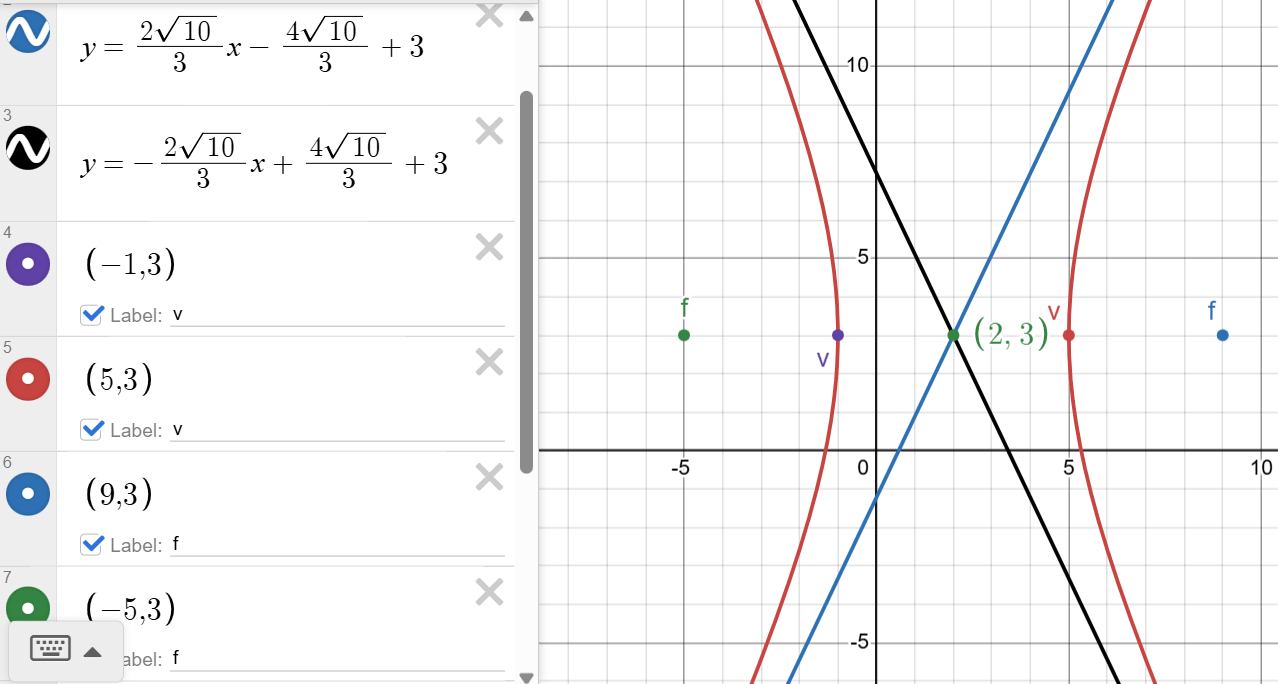
Graph and identify all the parts of the hyperbola
frac((x-2)^2)9- frac((y-3)^2)40=1
500
Find an equation of the circle tangent to both coordinate axes and the line x = -8.
(x+4)^2 +(y-4)^2 = 16 or (x+4)^2 +(y+4)^2 = 16
500
Suppose that a = b in the equation x2/a2 + y2/b2 = 1. What is the value of c? Where are the foci? What special ellipse is this?
c is 0 so the foci are at the origin and it is a circle.
500
Graph x - 11 = y2 + 6y
Vertex: (2,-3)
Horizontal parabola facing to the right
500
How can you identify each conic from mathematical context clues?
Great question! Many answers!