90
Find m∠ADB.
62
Find m∠DAB in ⨀C.
90
Find the measures of the angle a. Use the figure on the right.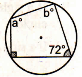
m<a = 108
An arc measuring one-half the circumference of a circle.
SEMICIRCLE
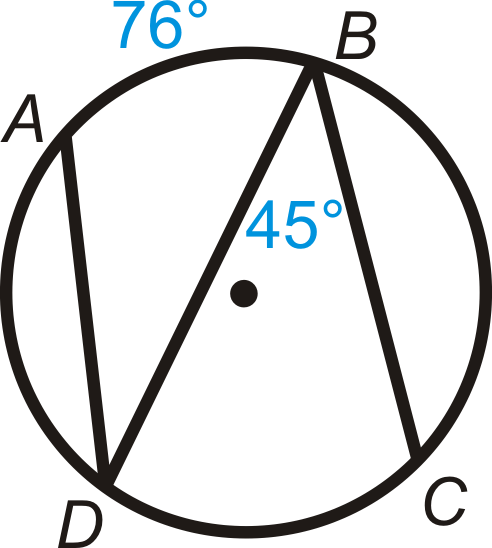
Find m∠ADB.
38
Find m∠ACB.
62.
A line segment with one endpoint in the center of the circle and one point on the circle.
What is a radius?
This is the relationship between opposite angles of a quadrilateral inscribed in a circle.
They are Supplementary
An angle formed by two rays whose vertex is the center of the circle.
CENTRAL ANGLE
Find the value of x in ⨀A.
51
This is the relationship between two adjacent arcs that cover the entire circle.
What is sum to 360 degrees?
This is the size of the angle inscribed in a semicircle.
right angle
Two chords are each measured as 36 centimeters long. One chord is 16 centimeters from the center. This is the distance the second chord is from the center.
What is 16 centimeters?
An angle whose vertex is on a circle and whose sides contain chords of the circle.
INSCRIBED ANGLE
Find the value of x in ⨀A.
46
Solve for x.
x = 37
An angle with the vertex on the circle, formed by two chords.
What is an inscribed angle?
The sides of an inscribed angle are ___________________.
chords
An arc that lies in the interior of an inscribed angle and has endpoints of the angle.
INTERCEPTED ARC
This is the relationship between opposite angles of a quadrilateral inscribed in a circle.
1/2 arc = angle
This is the relationship between central angles and the corresponding arc formed by the radii.
What is congruent?
Solve for x.
x = 42
If a chord, measuring 20 inches, is bisected by a line segment starting at the center and the radius is 26 inches, this is the length of the line segment.
What is 24 inches?
Semicircle Theorem: An angle intercepts a semicircle if and only if it is a(n) ____ angle.





