Functions & Graphs
Logs & Exponentials
Algebraic Manipulation
Rational Functions & Asymptotes
Distance, Roots & Miscellaneous
100
If f(x) = 4x−3, evaluate f(−2).
f(−2) = −11
100
Solve for x: log2x=3
x=8
100
Simplify: x2-9/x-3
x+3, x cannot = 3
100
Identify the vertical asymptote of y=5/x−6.
Vertical asymptote: x=6
100
Find the distance between (2, 2)(6, 5)
Distance =5
200
Find the slope of the line passing through (3, -1) and (7, 5).
Slope = 3/2
200
Rewrite as a single log: log a + 2logb
log(ab2)
200
Express as a trinomial: (x−7)(x+4).
x2−3x−28
200
Find the horizontal asymptote of y = 3x2-4/x2+7
Horizontal asymptote: y=3
200
Solve: 5/x+3=1/2.
x=7
300
The graph of y = f(x + 4) is the graph of f(x) shifted in what direction?
Shifted 4 units left
300
Solve: log5(x−1) = 2.
x=26
300
Perform the operation: x+2/x-1 - 3/x
x2-x+3/x(x-1)
300
State all solutions to x2−4x−12 = 0
Solutions: x = 6 and x = -2
300
Solve for x: sqrt(x+5) = 3.
x=4
400
Find the inverse of the function y=3x−9y.
f-1(x) = x+9/3
400
Solve: 32x-1=81.
x=5/2
400
Factor completely: 4x2−25.
(2x−5)(2x+5)
400
Express as a single fraction: 4/x+2 + 1/x-1.
5x-2/(x+2)(x-1)
400
Write 8/3−i in a+bi form.
12/5 + 4/5i
500
Solve: If f(x)=x2+5x, find f(x+h).
f(x+h)=x2+2xh+h2+5x+5h
500
Simplify: 1/2log a − 3log b.
1/2 log a − 3 log b = log (sqrt(a)/b3)
500
Solve the inequality: |3x+1| < 8.
−3< x < 7/3
500
Determine the domain of f(x)=x+1/sqrt(x-9)
Domain: (9,∞)
500
Solve the system: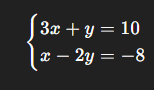 
(x, y) = (12/7, 34/7)