Functions
Quadratics
Polynomials
Rationals
Exponentials & Logarithms
100
The domain and range.
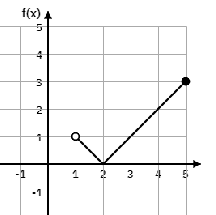
WHAT IS D:(1,5] and R:[0,3]?
100
The graph of this function is a parabola.
What is a quadratic function?
100
The highest power of the variable in a polynomial function.
What is the degree of a polynomial?
100
These are found by factors that are in the numerator.
What are the zeros?
100
Logarithms are inverse functions of this kind of function.
What are exponential functions?
200
Let ƒ(x) = 2 + sgrt(x+1) and g (x) =2x - 4.
Find f(g(6)).
f(g(8)) = 5
200
When a function hits the x-axis, it is this kind of characteristic.
What is a root (or zero, or x-intercept)?
200
This function's end behaviors are the opposite.
This is a function with an odd degree.
200
These are found by dividing the leading term in the numerator by the leading term in the denominator.
What are the horizontal asymptotes?
200
Rewrite the following as an exponential.
logbx=y
What is by=x?
300
The inverse of f(x) = x^2 -4
f-1(x) = sqrt(x+4)
300
When a function goes straight through a root, it is said to be this kind of root.
What is a single root?
300
These are created when you can reduce a factor from the numerator and denominator.
What are holes?
300
You want to do this first when creating a table of values of a logarithm.
What is write it as an exponential expression?
400
When a function bounces off a root, it is said to be this kind of root.
What is a double root?
400
These are determined by the factors in the denominator.
What are the vertical asymptotes?
400
When finding the inverse of a logarithm, you eventually have to do this with the x and the y.
What is switch them?
500
You use these values when writing an interval for when a graph is increasing or decreasing.
What are the x-values?
500
This skill is sometimes needed in order to determine the key characteristics of a rational function.
What is factoring?
500
What is the inverse of the following function?
log6(x+5)=y
What is 6x-5=y