String 'Em Along
Turtles All the Way Down
I'm Over Counting
Elementary, My Dear
Potpourri
100
A string of adjacent graph vertices that has each vertex exactly once, except the first is the last.
What is a Hamiltonian cycle?
100
The terms of this type of sequence are a function of earlier terms.
What is a recursive sequence?
100
The number of subsets of {0,1,...,9} that are not size 4.
What is
2^(10) - ( (10) ,(4) )
?100
Two sets with the same number of elements have this type of function between them.
What is a bijection? (invertible/one-to-one correspondence)
100
A partial order has these three properties.
What are reflexivity, transitivity, and antisymmetry?
200
These binary strings biject to non-negative integer solutions to
a+b+c+d+e = 148
What are strings with 5 ones and 148 zeros ending in a 1?
200
Inductive proofs are often phrased as having these three parts.
What are the base case, the inductive hypothesis, and the inductive step?
200
The number of faces and vertices of a planar graph are this many more than the number of edges.
What is 2?
200
Dilworth says the fewest number of chains needed to partition the elements of a poset is also this number.
What is the width or the size of the largest antichain?
200
Charles Babbage and Ada Lovelace are best remembered for their work on this unbuilt thinking machine.
What is the analytic engine?
300
The number of strings on alphabet {2,7,9} whose digits sum to n have this generating function.
What is
1/(1-(x^2+x^7+x^9))?
300
This recurrence relation has generating function
f(x) = ( a_0 + (a_1 - 3a_0) x ) / ( 1 - 3x + 2x^2 )
What is
a_(n+2) = 3a_(n+1) - 2a_(n)
?
300
Including and excluding functions gives this formula for the number of surjections
20 ->18.
What is
sum_{k=0}^18 (-1)^k ((18),(k)) (18-k)^(20)?
300
These are the elements of a maximal matching in this bipartite graph made by connecting the words SI, IS, AT, AS, SIM to the letters they contain.
What are {SI,S} {IS,I} {AT,T} {AS,A} and {SIM,M} ?
300
The symmetry group property that a set of derangements fails to have.
What is closure under composition?
(There's also no identity.)
400
Prufer says the trees with vertex set V biject to these strings.
What are strings on V of length |V|-2?
400
Eig-ad! A linearly recursive sequence is always big O of this characteristic quantity.
What is
O( n^(m-1) lambda^n)
where
lambda
is the largest eigenvalue and has multiplicity m.
400
The least weight closed covering walk on the following graph is this much more than the total weight of the graph.
What is 5?
400
Kuratowski says a graph is planar if and only if its set of subgraphs has no element homeomorphic to this.
What is the complete graph K_5 or the complete bipartite graph K_3,3?
400
The 26 letter English alphabet has this many partitions.
What is
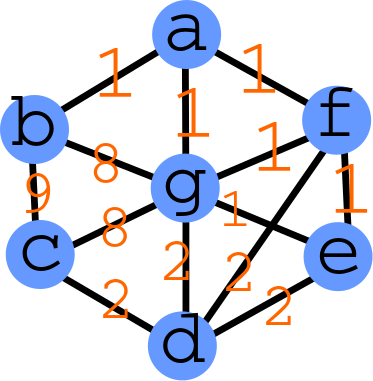
B_{26} = \sum_{k=1}^{26} {(26),(k):}}?
500
This function of n is the number of decimal strings of length n where an even digit is never followed by an odd digit.
What is
a_n = (1+n)5^n
?It satisfies a_0 = 1 and a_1 = 10 and the recurrence relation
a_n = 10 a_{n-1}-25a_{n-2}
500
This is a proof that every tree is 2-colorable.
What is
"As a base case a single vertex is 2-colorable. Suppose that every tree with k vertices is 2-colorable. Let T be a tree with k+1 vertices. Then T must have a degree 1 vertex v attached to some vertex u. By the inductive hypothesis deleting edge {u,v} and v from T gives a 2-colorable graph. Then coloring v the color u is not colored gives a 2-coloring of T."
?
500
The total number of length 10 strings on {a,b,c,d} is more than this number of strings on {a,b,c,d} considered up to cyclic permutation. ( Cyclic permutation: abc ~ bca ~ cba )
What is
( 4^10 + 4 * 4^5 + 4^2 + 4*4 ) / 10?
500
The color set of any proper coloring of this graph would need at least this many elements. (Proper means no adjacent vertices are colored the same color.)
What is 4?
500
Summing the slope one diagonals of Pascal's triangle would result in these numbers.
What are the Fibonacci numbers?