Exponents
Simplifying complex numbers
Basic solving
Quadratics
100
Simplify
3x^5*6x^4
18x^9
100
Simplify
(3+2i)+(7+11i)
10+13i
100
Solve
x^2+10=-6
x=4i
x=-4i
100
How many real solutions does the graph have
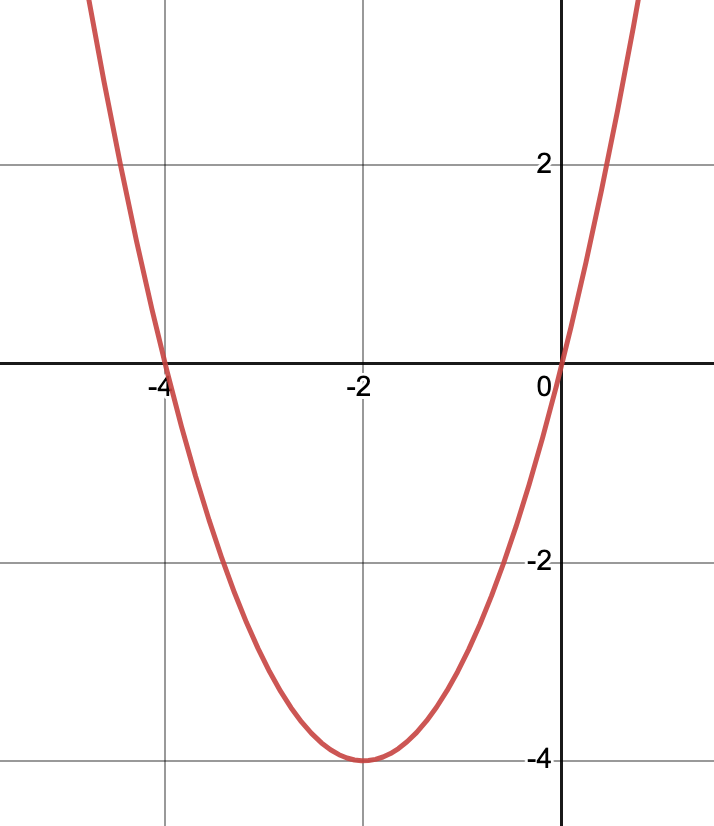
Two real solutions
200
Simplify
(2x^3)^4
16x^12
200
Simplify
i^32
1
200
Solve
sqrt(x)+2=11
x=81
200
Fill in the blank so the following is a perfect square
x^2+14x+ ____
49
300
Simplify
(8x^7)/(4x^10)
2/x^3
300
Simplify
-6i(6+2i)
12-36i
300
Solve
2x^2+4=30
x=sqrt13
x=-sqrt(13)
300
How many real solutions does the following equation have?
x^2+4x+12=0
No real solutions
400
Rewrite with roots
x^(4/3)
root(3)(x^4)
400
Simplify
(8-3i)(2+9i)
43+66i
400
Solve
2sqrt(x+4)+2=14
x=32
400
Solve by using the quadratic equation
x=(-b+-sqrt(b^2-4ac))/(2a)
3x^2+5x-2=0
x=.33
x=-2
500
Rewrite with ONLY exponents
1/sqrt(x^5)
x^(-5/2)
500
Given p=2+3i and k=5-2i
Simplify the following in the form a+bi
- k+p
- k-p
- k*p
7+i
3-5i
16+11i
500
Solve
(x-5)^2=-36
x=5-6i
x=5+6i
500
Solve by completing the square
x^2-8x+17=0
x=4+i
x=4-i