Challenge
Attributes
Inverses
f(g(x))
g(f(x))
100
How could you describe the domain for a situation dealing with time?
A. t = 0 B. t
0
C. t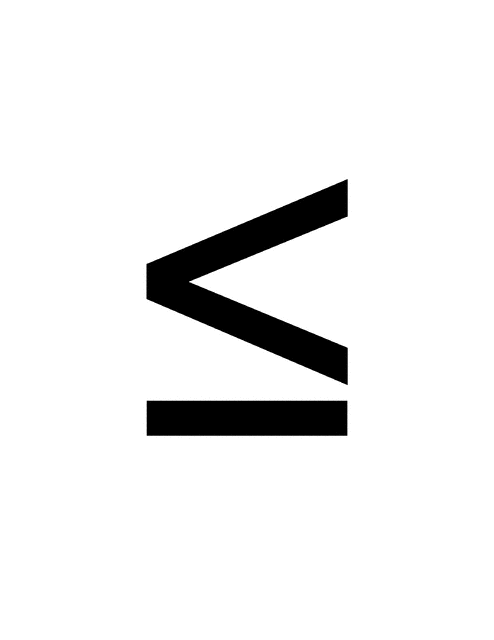
0 D. t is
Since time is positive, you must state that the domain, t0.
100
What is the minimum for y = x2 - 3?
How do you know?
The minimum is -3 because the graph shifted down.
-3 is the lowest y value on the graph, therefore, the minimum.
100
Choose the correct answer. Give examples.
The Inverse of a Function is (always, sometimes, or never) a function.
The inverse of a function is sometimes a function.
Ex: The inverse of a quadratic is NOT a function.
Ex: The inverse of square root is a function.
100
f(x) = 3x g(x) = -4
f(g(x))= -12
100
f(x) = 4 g(x) = -4x
g(f(x))=-16
200
If you buy a $20 pizza and split the cost with up to 5 people represented by x, what is the range of this situation in inequality notation?
f(x) = 20/x
Since $20 dollars is the total amount and the cost cannot be negative, the range would be:
range: 0 < f(x)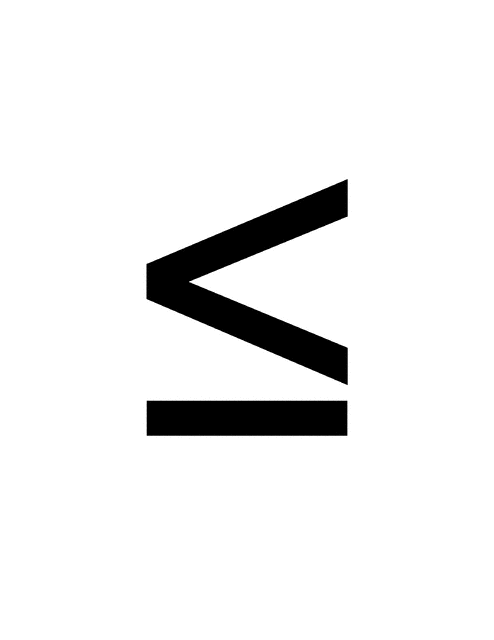20
Also, dividing by 0 is undefined, so the 0 is NOT included!
200
True or False?
The domain and range of a continuous step function are........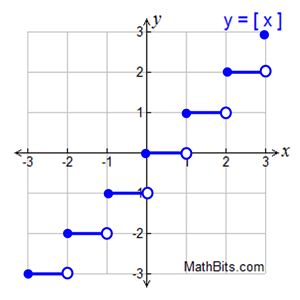
Domain: All real numbers Range: All Integers
True, the domain include all real numbers and the range includes positive and negative numbers, or integers only.
200
Choose an answer. Give an example.
A function and its inverse reflect across the (x-axis, y-axis or y=x).
A function and its inverse reflect across y=x.
On the logo project, your logo reflects the diagonal line, y=x.
200
f(x) = 4x-5 g(x) = x-3
f(g(x))=4x-17
200
f(x) = 2x g(x) = -3x2
g(f(x))=-12x2
300
List 4 ways to tell if two equations are inverses.
1. Do their graphs reflect y=x?
2. Are their x and y table values switched?
3. To find the inverse switch the x and y values in the equation and solve for y.
4. Will function composition result in x only?
300
How do you find the x and y intercept of a function?
Put the equations in y=, then find the zeros on the table. For the y-intercept, the x = 0. For the x-intercept the y = 0.
Put the 0 in for y in the equation and solve for x. Put the 0 in for x in the equation and solve for y.
Find the intersections on the graph!
300
True or False?
1. If f(a) = b, then f-1(b) = a.
2. For inverses the domain and range switch values from the original graph.
1. True, This means the x and y switch places for the inverse of the original, as a and b.
2. True, The domain and range switch just as the table values switch their x and y places. This creates an equal distance from the line of reflection, y=x.
300
f(x) = 2x-4 g(x) = x2-3
f(g(x))=2x2-10
300
f(x) = x2+4 g(x) = 2x-7
g(f(x))=2x2+1
400
Do these two equations represent inverse functions?
f(x) = 5 x - 7 f-1(x) = 1/5 x + 7/5
How do you know?
Yes
If you put both equations in y =, you will see that they reflect the line y=x on the graph.
If you switch the x and y of f(x) and solve for y, you get f-1(x) = 1/5 x + 7/5.
400
1. What is the possible domain for the ages in class?
2. What is the possible range for the numbers of students in class?
1. The domain of the student ages in class are:
{14, 15, 16, 17}
2. The range of numbers of students in class is:
{ 26, 28, 29, 29}
400
True or False?
1. Inverse points reflect the line of symmetry, y = 0.
2. Inverse ordered pairs of (x,y) are the same as the original, except you change the signs.
1. False, they are symmetrical about y=x.
2. False, the inverse has ordered pairs of (x,y) that are switched, but THE SIGNS DO NOT CHANGE!
400
f(x) = 3x-4 g(x) = x2-3
f(g(x))=3x2-13
400
f(x) = 2x2-4 g(x) = -3x+1
g(f(x))=-6x2+13
500
f(f-1(x)) = ?
(f o f-1)(x) = ?
f(f-1(x)) = x
(f o f-1)(x) = x
500
Why do we restrict the domain of the inverse for square root equations?
A square root function includes only one side of the parabola, so we must restrict the domain on the quadratic equation so only one side of the parabola remains.
500
True or False?
With function composition, you switch the x and y values and solve for y.
False
With function composition, you substitute one function into the other and simplify.
When finding the inverse, you switch the x and y values and solve for y.
500
f(x) = -3x2+5 g(x) = x-3
f(g(x))=-3x2+18x-22
500
f(x) = -3x+4 g(x) = x2-12
g(f(x))=9x2-24x+4