Valid "Reasons"
Congruence "Tricks"
Quadrilateral Properties
Proof Structure
100
Each statement in a proof must be accompanied by a valid _________.
A Reason is a given fact, a definition of a property of mathematics, or a mathematical theorem which defends the statement.
A statement answers "What"
A Reason answers "Why"
100
If a triangle has two congruent sides, what other congruences must also be true?
Two Congruent Angles, that are opposite to the congruent sides.
An Isosceles Triangle has two congruent sides and two congruent angles.
100
What is a property that all quadrilaterals share?
4 sides and 4 angles
100
What should the first line of a proof always be?
Rewrite all the given information in the problem, and state "given."
200
In the following statement-reason proof, fill in the missing box
Statement #1 is valid because it was GIVEN to us in the problem
200
Given
\overline(AB) ⟂ \overline(CD)
Provide two reasons that prove
angle ABC cong angleABD
Statement Reason
Definition of Perpendicular Lines
All right angles are congruent
200
Two students look at the properties of a quadrilateral. Johnny says that the shape has all the properties of a rectangle, Dylan says that the shape has all the properties of a Rhombus. If both Johnny and Dylan are correct, what shape are they both describing.
A Square
The quadrilateral hierarchy shows us that a square has all the properties of a Rectangle and a Rhombus.
200
Does the order of steps matter for a proof? Why or why not?
Yes, you need to make sure that you have prove some information is true before you can prove that other information is true.
300
Provide a congruence statement and a reason for the two triangles above
triangle ABC cong triangle XYZ
triangle CBA cong triangle ZYX
triangle BCA cong triangle YZX
Reason: Side-Angle-Side Congruence
300
For Parallelogram RYAN, what reason can be used to show that
angle 1 cong angle 2
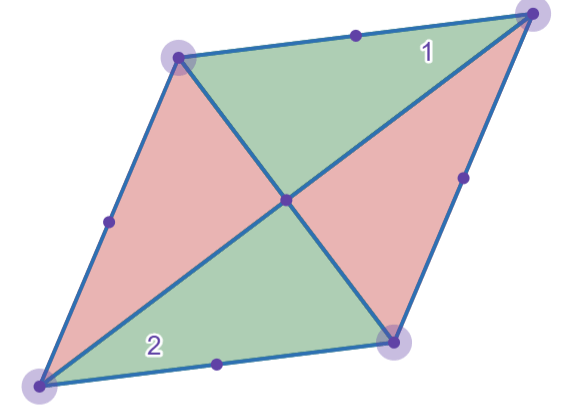
Alternate Interior Angle Theorem: If two parallel lines are cut by a transversal, the resulting alternate interior angles are congruent
300
A parallelogram ABCD has perpendicular diagonals, what type of parallelogram is it?
A Rhombus has diagonals that are perpendicular to each other.
300
What information is given in the diagram below
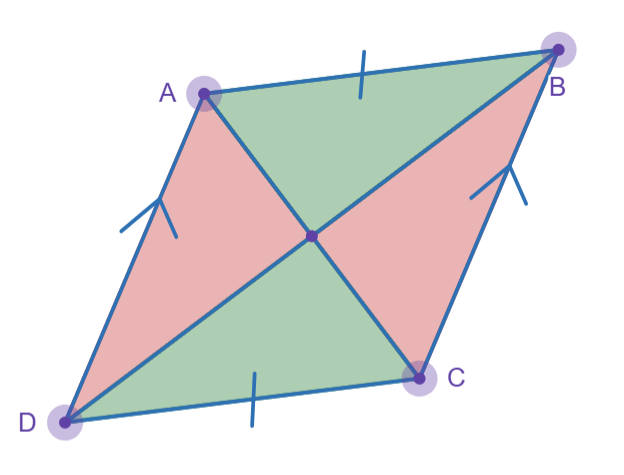
squareABCD
\overline(AB)cong\overline(CD)
\overline(DA)||\overline(CB)
400
Given that
triangle ABC cong triangle XYZ
What reason can we use to defend the statement
\overline(AB) cong \overline(XY)
Reason: Corresponding Parts of Congruent Triangles are Congruent
CPCTC
400
Two lines intersect at a point, they create two pairs of ______________.
Two pairs of congruent, vertical angles
400
If a quadrilateral has 1 pair of parallel sides what types of quadrilateral could it be?
Any quadrilateral COULD have 1 pair of parallel sides.
400
Given:
square ABCD
\overline(AB)cong\overline(CD)
\overline(AC)cong\overline(BD)
What is the most specific quadrilateral that
square ABCD
must be?
A Rectangle
At least one pair of opposite, congruent sides
Diagonals are congruent
500
What reason could be used to show that
angleA cong angleD
Alternate Interior Angle Theorem:
If two parallel lines are cut by a transversal, their alternate interior angles are congruent.
500
Give a reason why
\overline(AB)cong\overline(BA)
The reflexive property states that any object is congruent to itself.
500
Mr. Schade starts walking north on a parallelogram shaped field. He turns at the first two corners of the field he is walking on and stops on the third side. What direction is he now facing?
South!
If he walked around 2 corners, the corners must be consecutive. The consecutive corners of a parallelogram are supplementary. Supplementary angles add to 180!
500
Fill in the missing step in the following proof:
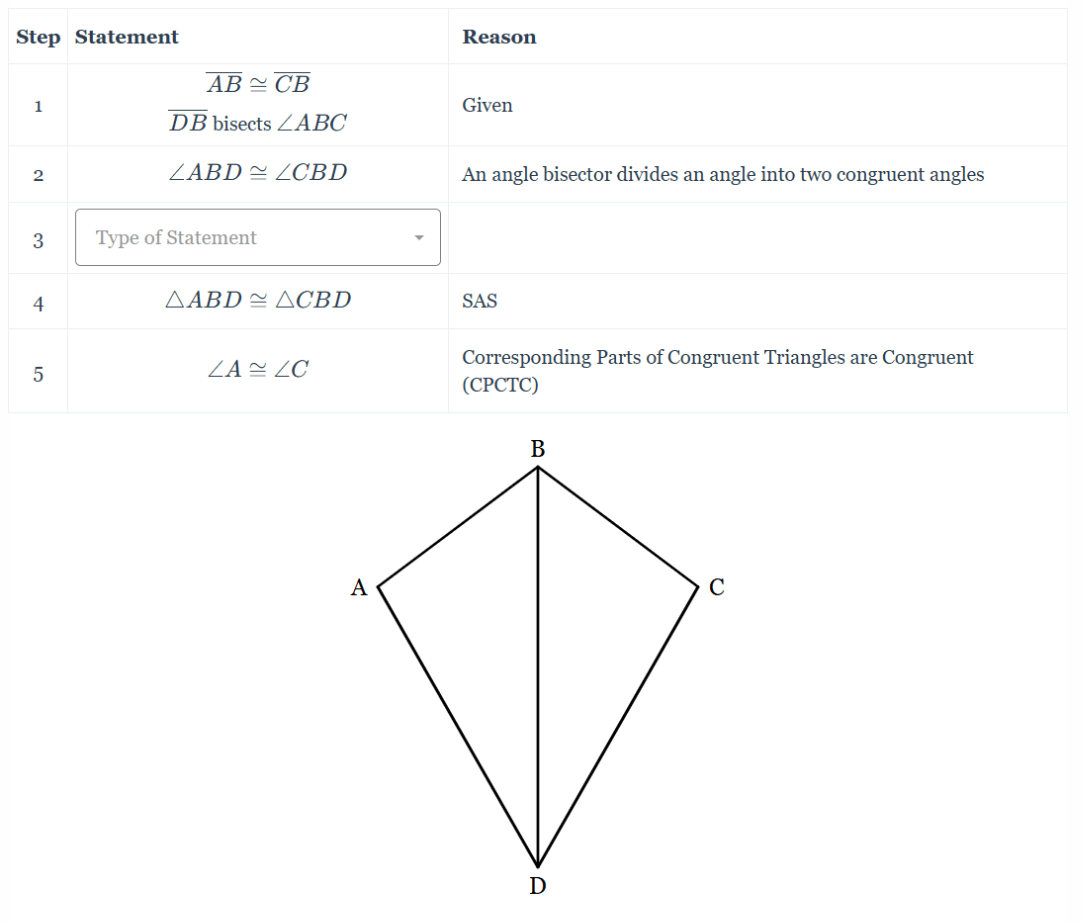
Statement:
\overline(BD)cong\overline(DB)
Reason: Reflexive Property.
Explanation: We know that we have to prove it using SAS, we already have a side, and an adjacent angle. So we just need to know that the other side adjacent to the angle is congruent.