SSS & RHS
SAS
AAS & ASA
Missing Info
Mixed Bag
100
Are these triangles congruent? If so, write the congruence statement.
△MPL ≅ △MNO (SSS) or (RHS)
100
Are these triangles congruent through SAS? If so, write the congruence statement.
Yes, they share the common side length of line segment BD.
AB = BC
BD is shared
Angle DBC = Angle DBA (Right angle)
△ABD ≅ △CBD
100
Are these triangles congruent? If so, which theorem can you use and write the congruent statement.
No, since the congruent sides are not in the same position.
The sides are across from different angles.
100
What info do you need to prove these congruent by SSS?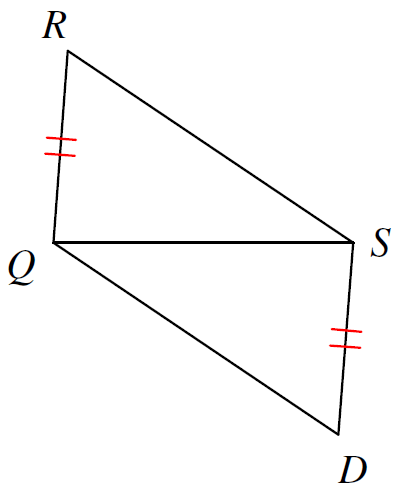
What is
RS \cong QD
100
Can you prove congruence? If so, write a triangle congruence statement and state which theorem you are using.
△KJL ≅ △HGF by HL
200
Can you prove these triangles are congruent through RHS? If so, write a congruence statement.
YZ = ST
XZ = RT
Angle Y = angle S (Right angle)
Triangle XYZ is congruent to Triangle RST (RHS)
200
Are these triangles congruent through SAS? If so, write the congruence statement.
CA = ZX
AB = XY
Angle C = Angle Z
Angle C and Angle Z are in the middle of two congruent sides
△BCA ≅ △YZX (SAS)
200
Are these triangles congruent through ASA? If so, write the congruence statement.
Angle ABD = Angle BDC
Angle ADB = Angle DBC
BD is shared
△ADB ≅ △CBD (ASA)
200
What info do you need to prove these congruent by SAS?
What is
JI \cong TS?
200
Solve for x.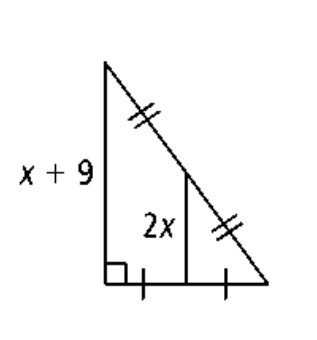
What is x = 3?
300
Are these triangles congruent through SSS? If so, write the congruence statement.
Not congruent through SSS
300
Is this an example of triangle congruence through SAS? If so, write a triangle congruence statement.
No, triangles are not congruent through SAS.
300
Do we have enough information to prove that these 2 triangles are congruent? If so, make a triangle congruence statement.
No, there is not enough information to prove they are congruent through AAS.
300
What info do you need to prove these congruent by ASA?
What is
DE \cong KJ
300
Can you prove congruence? If so, write a triangle congruence statement and state which theorem you are using.
△DEF ≅ △HIG by ASA
400
Can you prove congruence through SSS or RHS? Explain.
You can prove congruence through SSS because the shared side length is also congruent.
Cannot do RHS because they are not right triangles.
400
Label the triangle diagram below so that you could use SAS to prove it congruent.
Answers may vary
400
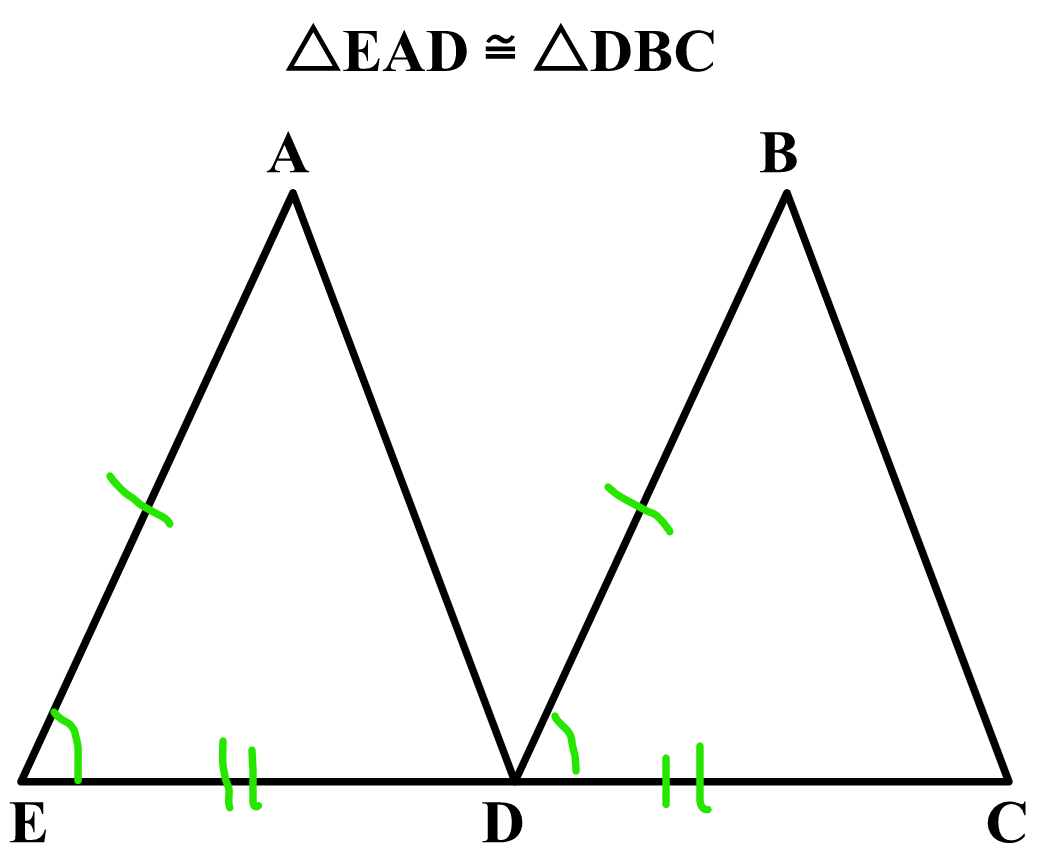
Are these triangles congruent through ASA? If so, write the congruence statement.
△BCA ≅ △EFD
400
What info do you need to prove these congruent by AAS?
What is
YZ \cong MN or XZ \cong LN
400
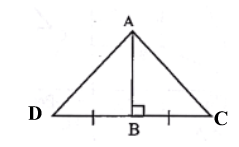
What special segment(s) is AB? Can you prove the two triangles are congruent? What theorem can you use?
What is an Altitude, a Median, & a Perpendicular Bisector?
△CBA ≅ △DBA by SAS
500
AC is an altitude. Explain how the triangles can be congruent.
Since AC is an altitude, <ACB = <ACD = 90 degrees.
Since AC is a shared side, by the reflexive property AC ≅ AC.
△ACB ≅ △ACD by RHS
500
Do we have enough information to prove that these 2 triangles are congruent through SAS?
Yes, the third angle will be congruent. Since 2 angles are already congruent, the third angle must be congruent as well. Additionally, the triangles share the third side length.
500
Are these triangles congruent through AAS? If so, write the congruence statement.
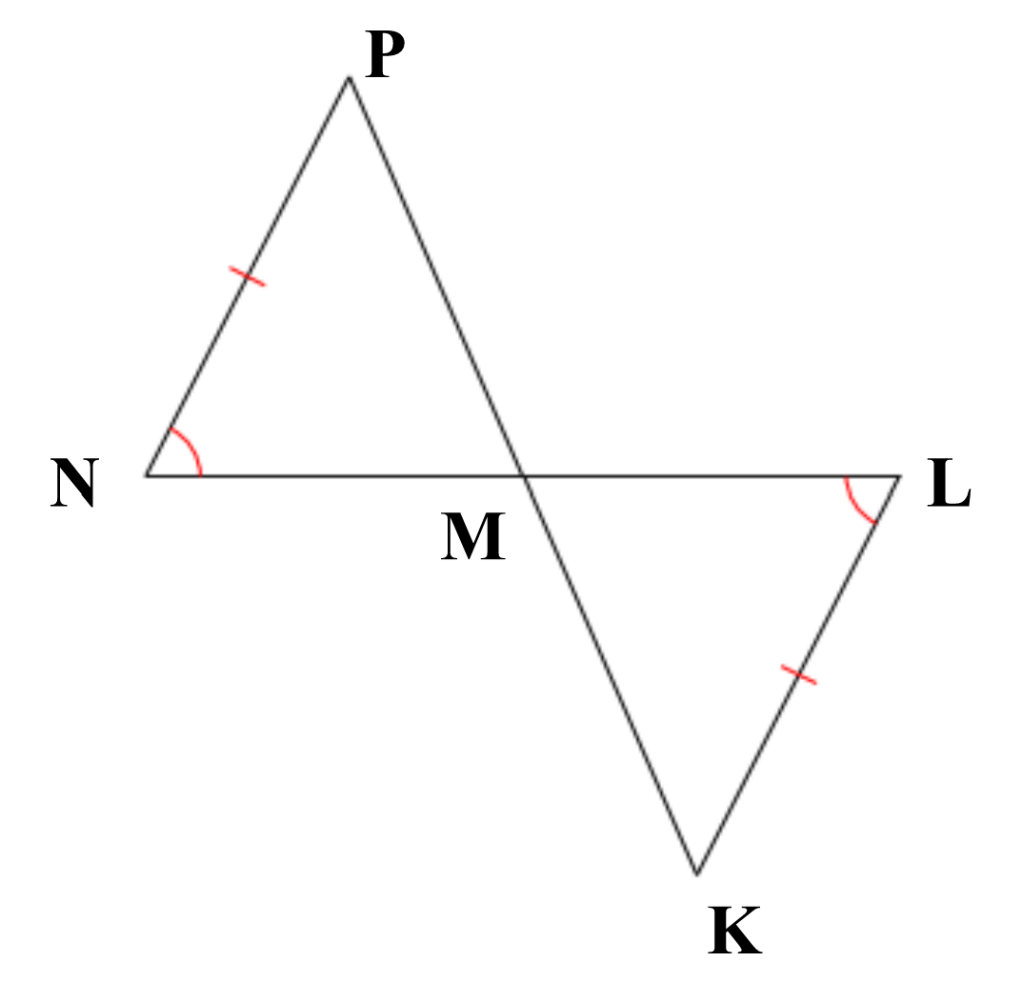
△LMK ≅ △NMP
500
Here is a cut gem. What side lengths do you need to know in order to prove congruence between the pink and green triangles?
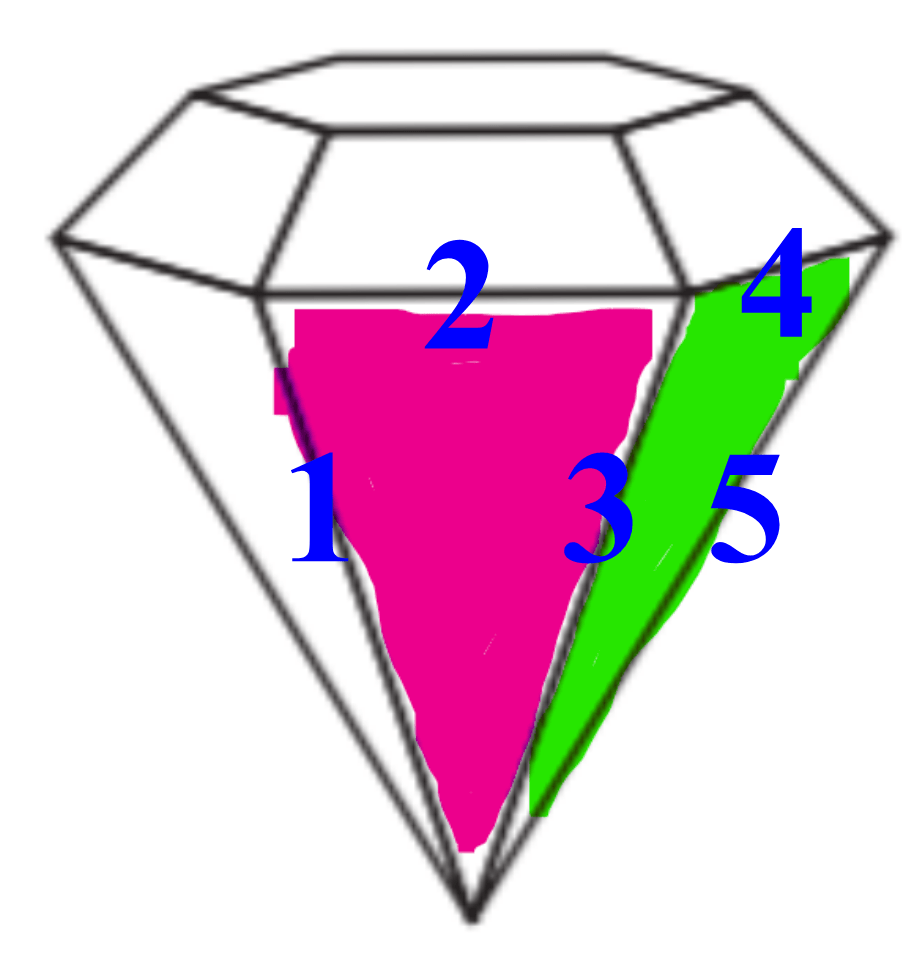
side 1 congruent to side 5
side 2 congruent to side 4
500
Are these triangles congruent? If so, write the congruence statement & state which theorem you are using.
Since BD is a shared side, by the reflexive property BD ≅ BD.
Since there are two pairs of congruent Angles, the third angles must also be congruent (180 theorem)
△BDA ≅ △DBC by SSS or SAS or AAS or ASA