Are these triangles congruent? If so, write the congruence statement.
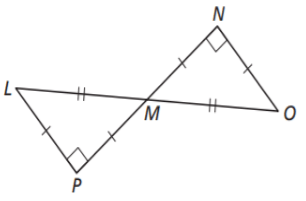
△MPL ≅ △MNO
Are these triangles congruent through SAS? If so, write the congruence statement.
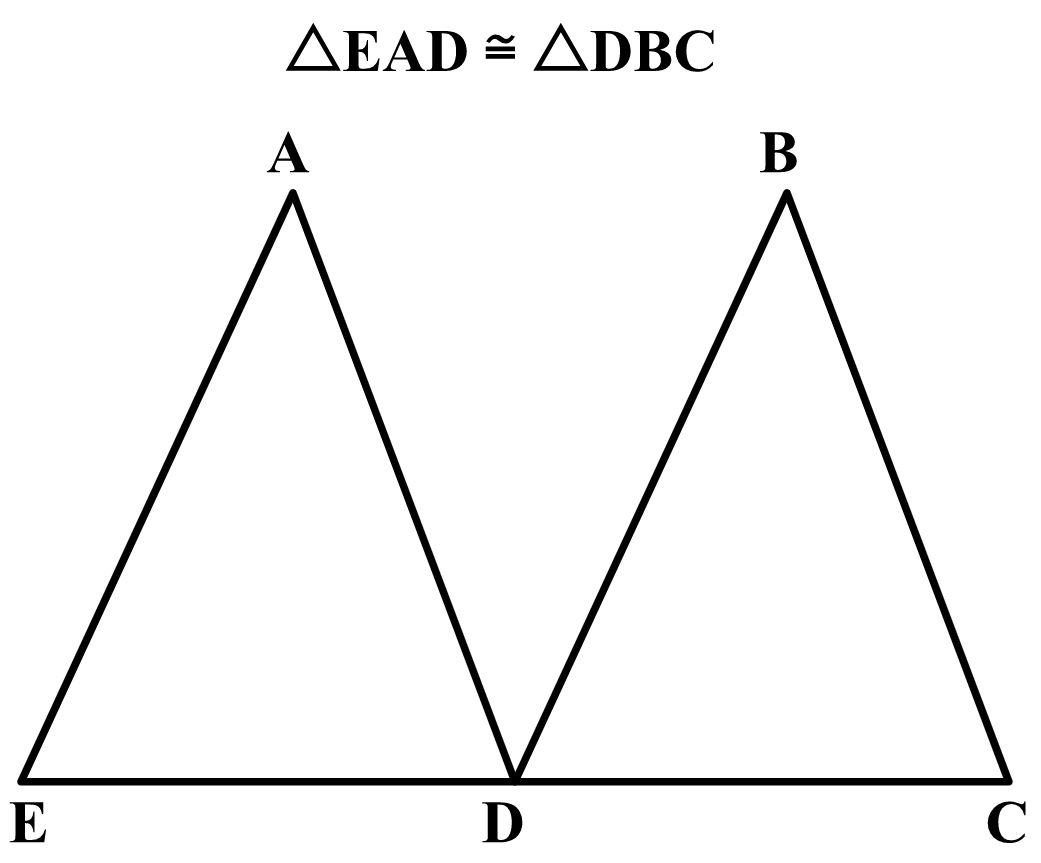
Yes, they share the common side length of line segment BD.
△ABD ≅ △CBD
Are these triangles congruent? If so, which theorem can you use and write the congruent statement.
No, since the congruent sides are not in the same position.
The sides are across from different angles.
What info do you need to prove these congruent by SSS?
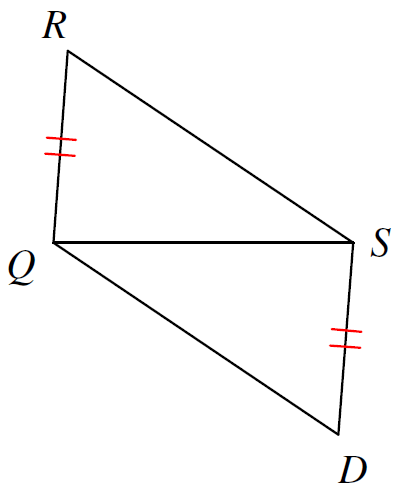
What is
RS \cong QD
Can you prove these triangles are congruent through HL? If so, write a congruence statement.
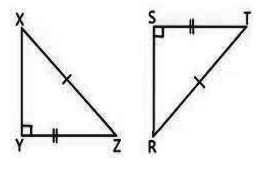
Yes, Triangle XYZ is congruent to Triangle RST.
Are these triangles congruent through SAS? If so, write the congruence statement.
△BCA ≅ △YZX
Are these triangles congruent through ASA? If so, write the congruence statement.
△ADB ≅ △CBD
What info do you need to prove these congruent by SAS?
What is
JI \cong TS?
Are these triangles congruent thru SSS? If so, write the congruence statement.
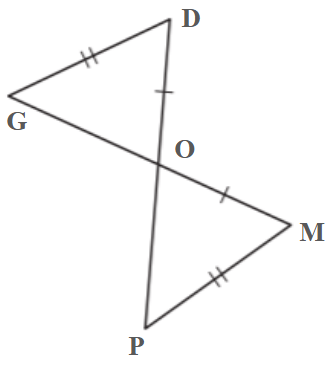
Not congruent thru SSS
Is this an example of triangle congruence through SAS? If so, write a triangle congruence statement.

No, triangles are not congruent through SAS.
Do we have enough information to prove that these 2 triangles are congruent? If so, make a triangle congruence statement.
No, there is not enough information to prove they are congruent through AAS.
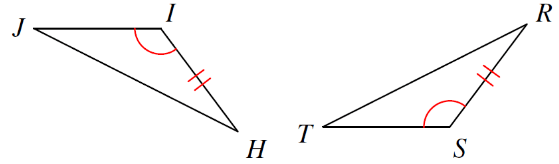
What info do you need to prove these congruent by ASA?
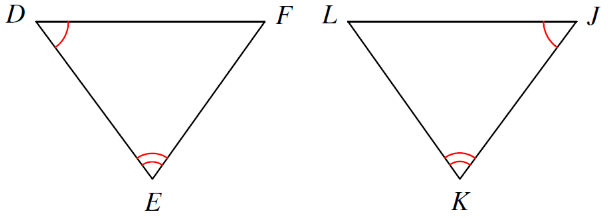
What is
DE \cong KJ
Can you prove congruence through SSS or HL? Explain.
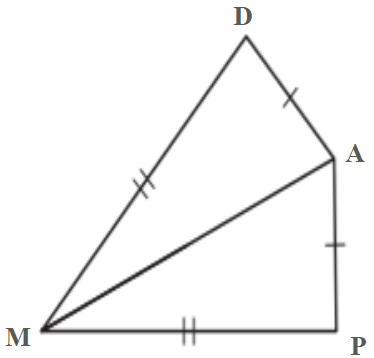
You can prove congruence through SSS because the shared side length is also congruent.
Cannot do HL because they are not right triangles.
DOUBLE JEOPARDY
Label the triangle diagram below so that you could use SAS to prove it congruent.
Answers may vary
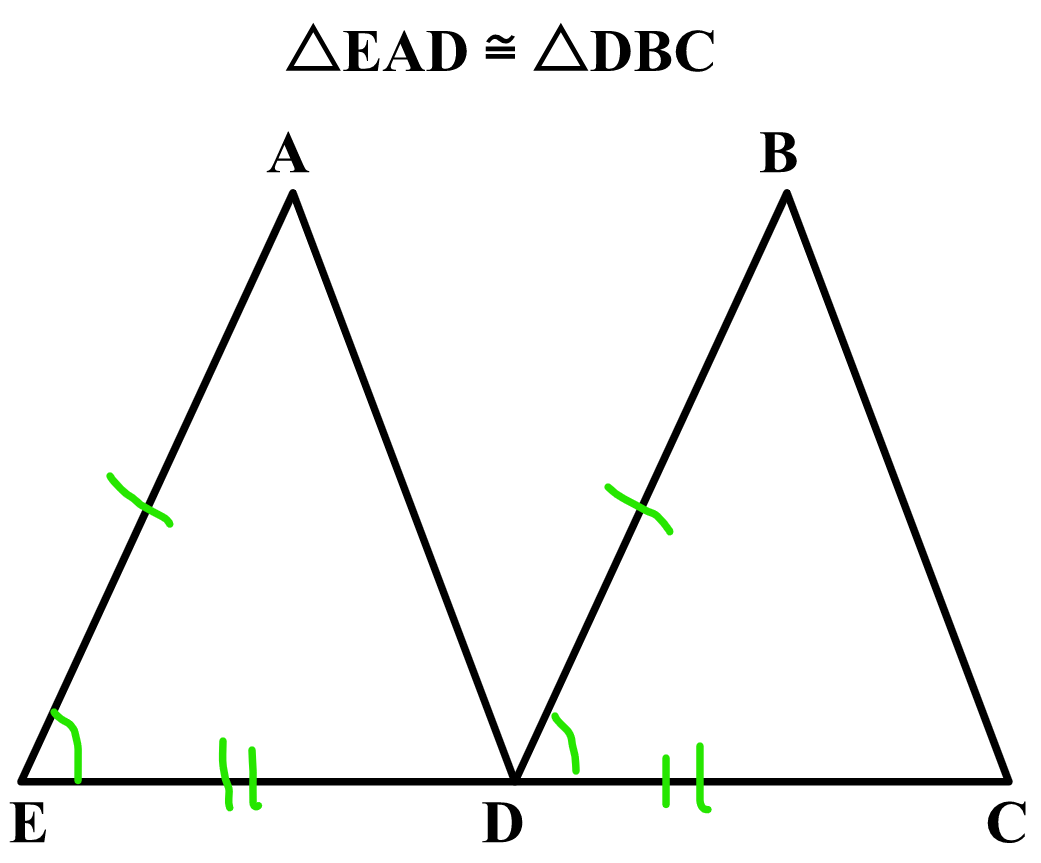
Are these triangles congruent through ASA? If so, write the congruence statement.

△BCA ≅ △EFD
What info do you need to prove these congruent by AAS?
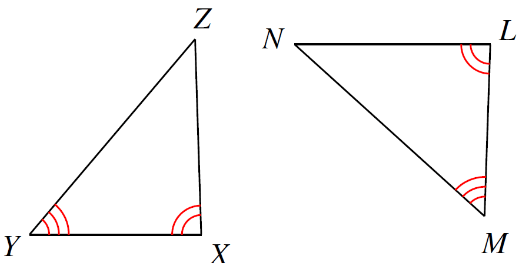
What is
YZ \cong MN or XZ \cong LN
AC is an altitude. Explain how the triangles can be congruent.
Since AC is an altitude, m<ACB = m<ACD = 90 degrees.
Since AC is a shared side, by the reflexive property AC ≅ AC.
△ACB ≅ △ACD by HL
Do we have enough information to prove that these 2 triangles are congruent through SAS?
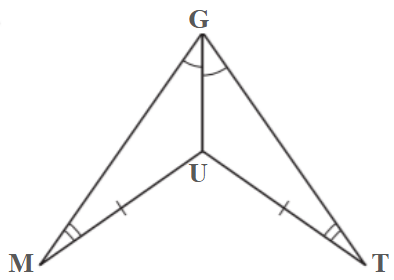
Yes, the third angle will be congruent. Since 2 angles are already congruent, the third angle must be congruent as well. Additionally, the triangles share the third side length.
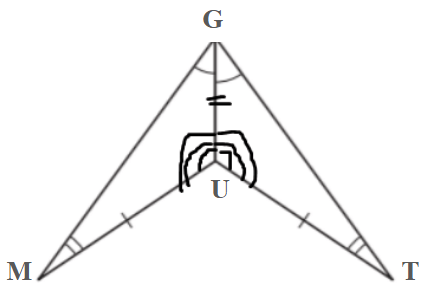
Are these triangles congruent through AAS? If so, write the congruence statement.
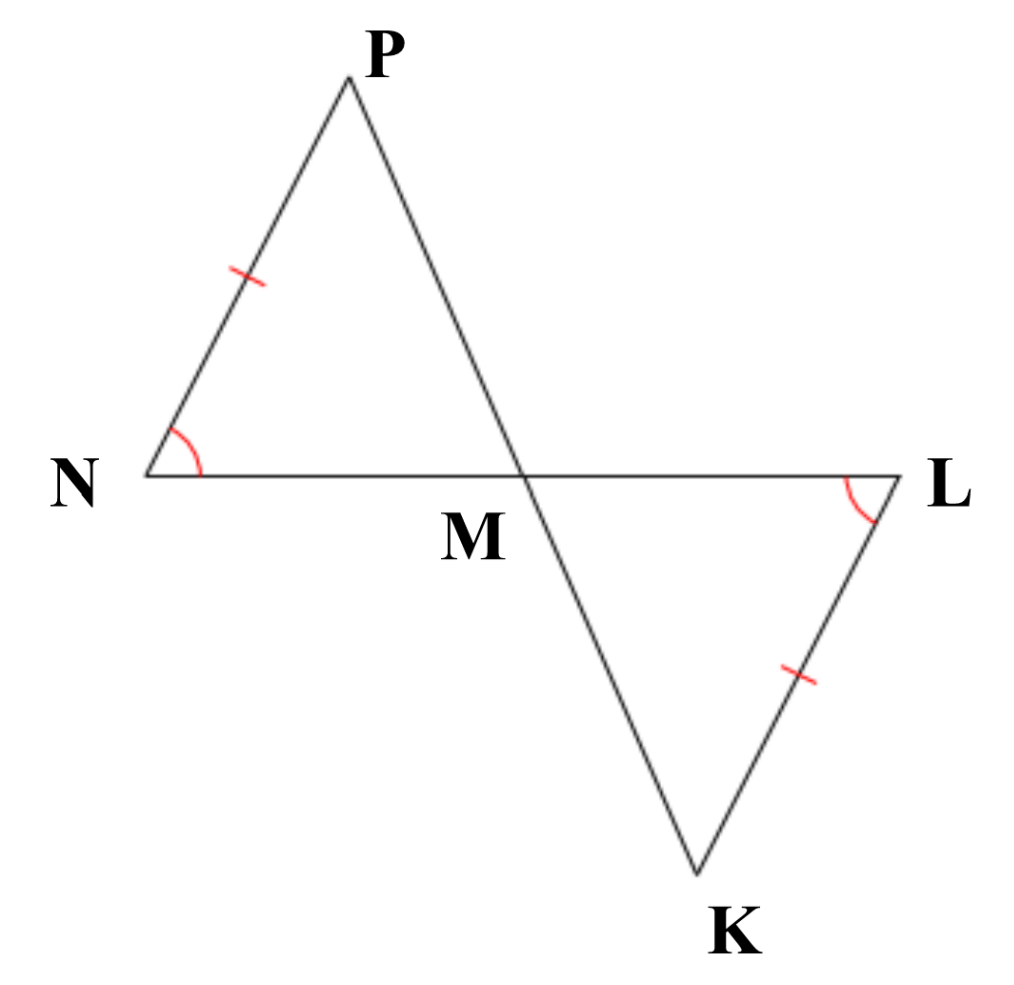
△LMK ≅ △NMP

