Determine wether the following shapes are polygons. If they are, classify them.
1. 
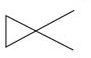
2. 
3. 
1. Yes; a pentagon
2. No, it is not closed
3. No, it does not contain 3 or more line segments
Each of these points represents an object. Find the distance between these 2 points on the coordinate plane. Note, each unit represents 10 meters. 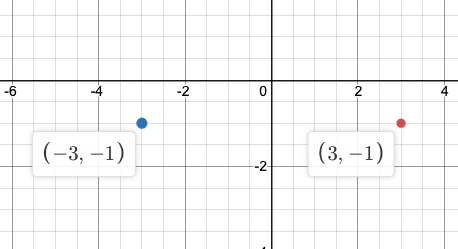
Counting the boxes, we see the 2 points are 6 units away. Since each unit represents 10 meters, the objects are 60 meters away.
Find the area of these parallelogram's in square units.
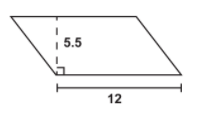
#1
#2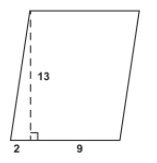
A=b\cdoth
where b is the base and h is the height.
#1
A=12*5.5=66 \ units^2
#2
Make sure to first find the total length of the base (which is 9+2=11).
Now,
A=11\cdot13=143 \ units^2
A right triangle has an area of 20 square meters, and a base length of 8 meters. What is its height?
A=1/2bh
Substituting the known values:
20=1/2(8)(h)
Simplifying:
20=4h
Dividing by 4:
h=5 \ meters
1. What is the distance between A(3,1) and B(3,8)
2. What is the distance between C(2,-1) and D(-4,-1)
1. 7 units
2. 6 units
Reflect these points across the x-axis:
A(3,-2)
B(1,4)
C(8,8)
What are the new coordinates?
The new coordinates after reflection are:
A(3,2)
B(1,-4)
C(8,-8)
Reflect these points across the y-axis:
A(3,-2)
B(1,4)
C(8,8)
What are the new coordinates?
A(-3,-2)
B(-1,4)
C(-8,8)
Find the area of the following triangles:
#1
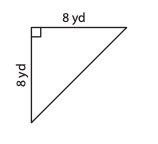
#2
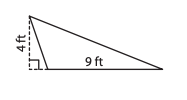
For a triangle,
Area=1/2b\h
#1
A=1/2(8\ yd) (8\ yd)=32\ yd^2
#2
A=1/2(4\ ft) (9\ ft)=18\ ft^2
One base of a trapezoid measures 12 meters, and the other base measures 8 meters. If the area is 144 square meters, what is the height of the trapezoid?
A=1/2h(b_1+b_2)
Substituting,
144=1/2h(12+8)
144=1/2(20)(h)=10h
Dividing by 10,
h=144/10=14.4 \ meters
The Shanghai World Financial Center is one of the tallest buildings in the world. It features a large trapezoidal opening to allow wind to pass through. The opening is about 35 meters tall. It is about 40 meters along the bottom and 50 meters along the top. What is the approximate area of the opening?

A=1/2h(b_1+b_2)
Substituting the numbers, we get:
A=1/2(35)(40+50)
Simplifying:
A=1/2(35)(90)=1/2(90)(35)
Solving:
A=45\times35=1,575 \ m^2
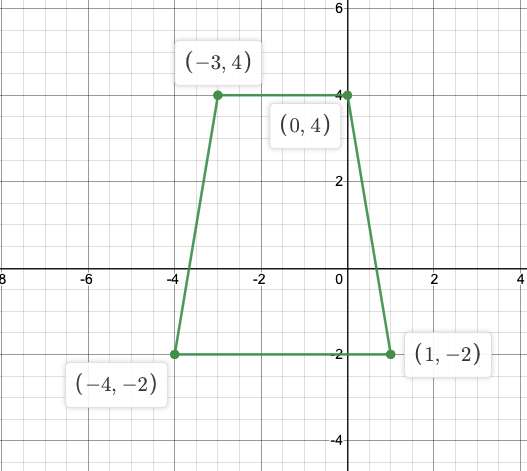
Graph the points A(-3,4), B(-4,-2), C(1,-2), D(0,4). Connect A to B to C to D to A. What names (at least 2) can you use to describe this figure?
- Polygon
- Quadrilateral
- Trapezoid
Find the area of the following composite figure: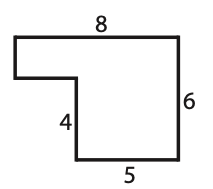
We can split this into two rectangles.
Area of 1st rectangle:
A=4\times5=20 \ units^2
Area of 2nd rectangle:
A=8*2=16 \ units^2
So, the total area is
20+16=36 \ units ^2
The area of a trapezoid is 65 square feet. If the height is 10 ft, what is the sum of the lengths of the bases?
A=1/2(h)(b_1+b_2)
We want to find the sum of the lengths of the bases, which is
(b_1+b_2)
Using our formula, we have that:
65=1/2(10)(b_1+b_2)=5(b_1+b_2)
Dividing both sides by 5, we see that:
b_1+b_2=65/5=13 \ ft
So, the sum of the lengths of the bases is 13 ft.
A blueprint of a rectangular pool is shown.
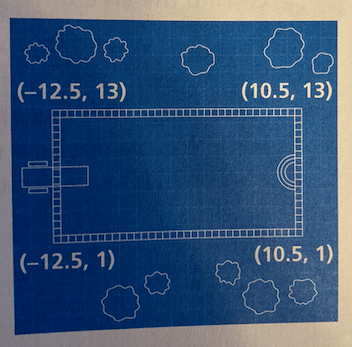
What are the area and perimeter of the pool?
The dimensions of the pool are 23 x 12.
Area=bh=23\cdot12=276 \ units^2
Perimeter=23+23+12+12=70 \ units ^2
Find the area of the shaded region. 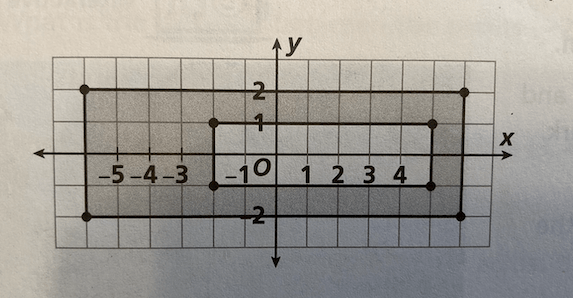
We need to subtract the area of the small rectangle from the large one.
A_{Small} = 2\times7=14 \ units ^2
A_{Larg e} = 4\times12=48 \ units^2
Thus, the shaded region has an area of
48-14=34 \ units^2
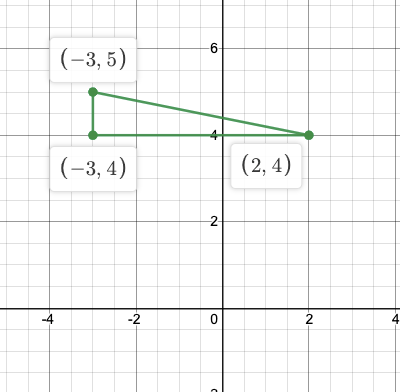
The coordinates of two vertices of a right triangle are A(-3,5) and B(2,4). What are the 2 possibilities for coordinates of vertex C if the figure formed is a right triangle?
Possibility #1
C=(-3,4)
Possibility #2
C=(2,5)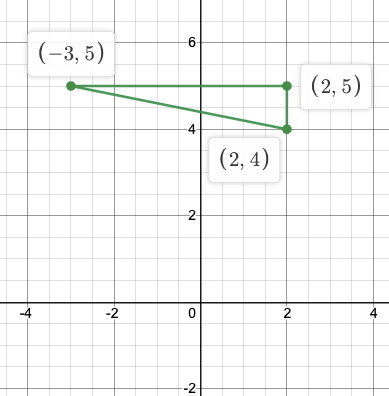
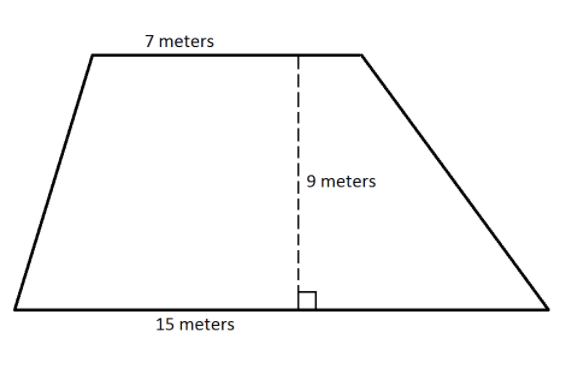
Find the area of the following trapezoids:
#1
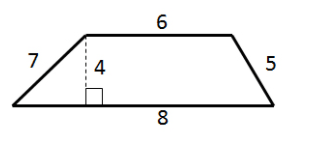
#2
A=1/2h(b_1+b_2)
#1
A=1/2(9)(15+7)=1/2(9)(22)
Simplifying,
A=11\times9=99 \ meters ^2
#2
First, identify
h=4, b_1=8, b_2=6
Now, using the above formula,
A=1/2(4)(8+6)=2(14)=28 \ units^2
Find the area of the following composite figure.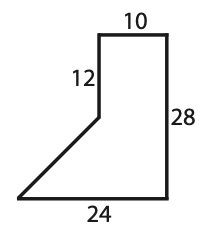
This can be split into a rectangle and a trapezoid.
The area of the rectangle is:
A=12\times10=120 \ units^2
The area of the trapezoid is:
A=1/2(16)(10+24)=8(34)=272 \ units^2
So, the total area is:
120+272=392 \ units^2
A trapezoid's larger base is 4 times the length of its shorter base. If it has an area of 70 square feet, and a height of 4 ft, what is the length of the shorter base?
b_1=
shorter base
4b_1=
longer base
So,
A=1/2h(b_1+b_2)
70=1/2(4)(b_1+4b_1)
Simplifying:
70=2\cdot5b_1=10b_1
Dividing by 10,
b_1=70/10=7
So, the shorter base is 7 ft.
A parallelogram's height is three times its base. If it has an area of 108 square feet, what are the lengths of its base and height?
Let x = base
Then, 3x = height
Area = base x height =
x\times3x=3x^2
Since we are given that the area is 108 square feet, we know that:
3x^2=108
Dividing both sides by 3, we see that:
x^2=36
Now, if you recall what squared means, you will realize that
6^2=36
so, x=6.
x=6 ft is the length of the base.
As we defined above, 3x is the height, so it is
3(6)=18ft
Find the area of the following composite figure.
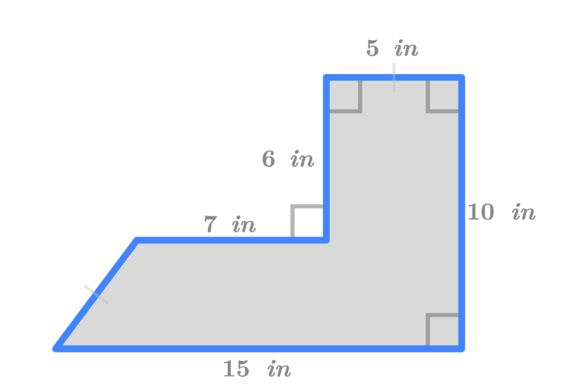
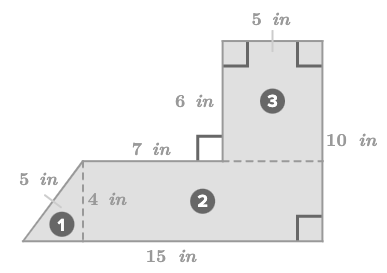
Labeling the figure, it now looks like the figure above. Note, the 3rd side of the triangle is 3 inches, and the 5 inches is not necessary to solve the problem.
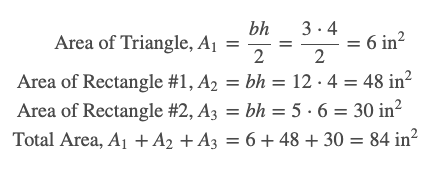 So, the total area is 84 square inches.
So, the total area is 84 square inches.
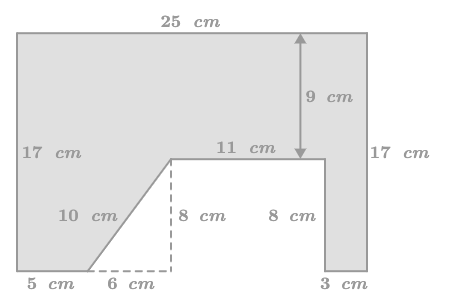
Find the area of the shaded figure below.
Hints
-You do not need all the numbers
-You should use the subtractive method (big area - small area)
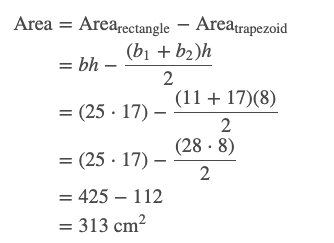
So, the area is 313 square centimeters.