What is the initial value in the following function:
f(x) = 1/2*(3/4)^x
1/2
What is the growth factor in the following equation:
f(x) = 3*2^x
2
There are 50 bacteria in a petri dish at the beginning of a science lab. Every hour, each bacterium splits into three bacteria. Write an equation that represents the number of bacteria, n, after t hours.
n = 50 *(3)^t
The amount of bacteria in a petri dish is 100. The bacteria population will double every hour. How many bacteria will be in the dish after 2 hours? Show or explain your work.
100*2^2=400
Or
100 X 2 X 2 = 400
400
A student takes a test that is 50 questions. The student gets 80% of the questions correct. How many questions did he get right? Show or explain you reasoning.
40 questions correct.
A car's price p is a function of the number of years, t, since it was purchased. The function is
p(t) = 18,000*(4/5)^t
What is the "a" value of this function? What does it mean in this situation?
The "a" value is 18,000. It is the price of the car when it was first purchased.
Mold growth that covers an area of 64 square feet is treated so that the mold can die off. Every day, the amount of mold decreases by 1/9 of what is what the day before. What is the decay factor in this situation?
8/9
Brenda gets 100 dollars for her birthday. She spends 1/4 of the money the 1st week. Every week, she continues to spend 1/4 of the money she had the week prior. Write an exponential equation to represent this situation.
y=100*(3/4)^x
f(x) = 100 *(3/4)^x
Given the following equation
f(x)=6*(1/4)^x
find f(2). Show or explain your work.
6*(1/4)^2 = 0.375
(1.20) x 10,000 = 12,000
or
10,000 + (0.20) 10,000 = 12,000
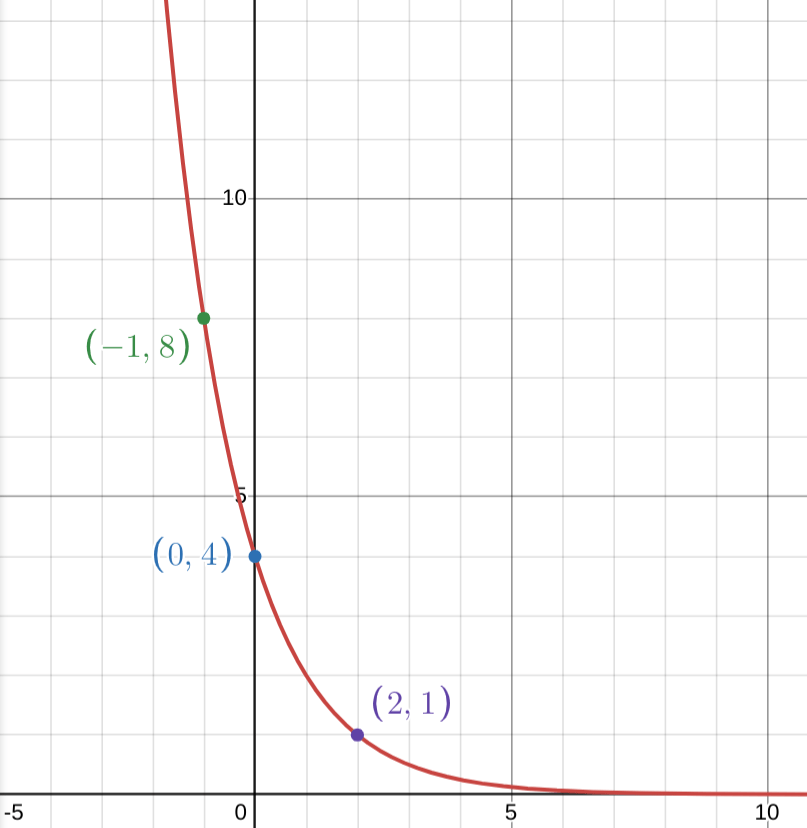
What is the a value of this function?
3
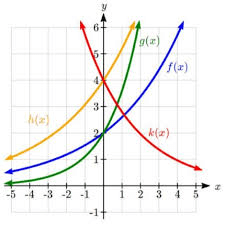
Which of these functions would have a b value that is less than 1? Explain how you know.
K(x) because it is the only decreasing
The following equation represents the population in a given area x years after 1990:
f(x) = 90,000*1.5^x
What would f(-2) mean in this situation?
The population two years before 1990
The following equation represents the population in a given area x years after 1990:
f(x) = 90,000*1.5^x
What does f(-2) equal? Show or explain how you know
f(x) = 90,000*1.5^-2
40,000 people
A local clothing store is running a sale where all items are 30% off. If a shirt costs $45, what is the cost of the shirt after the sale? Show or explain your reasoning.
(0.70) x 45 = 31.50
OR
45 - (0.30) x 45 = 31.50
$31.50
The amount of medicine in a person's bloodstream is measured a few hours after they took the medication using a blood test. This situation can be modeled as a function of time using the following equation:
m(t) = 500 *(1/4)^t
What does the 500 tell us in this situation?
How much medicine is in their bloodstream when they take the blood test.
The amount of medicine in a person's bloodstream is measured a few hours after they took the medication using a blood test. This situation can be modeled as a function of time using the following equation, where t is the number of hours after the initial blood test:
m(t) = 500 *(1/4)^t
What does the 1/4 tell us in this situation?
That every hour, the amount of medicine in their bloodstream is going down by 3/4
OR
Every hour, the amount of medicine in their bloodstream is 1/4 of what it was the previous hour
Write the exponential equation that would represent this graph.
y = 4 * (1/2)^x
The following equation represents the population growth in t years after the year 2000.
f(t)=1000*(1.2)^t
Find the average rate of change between 2001 to 2003. Show or explain your work
(f(3) - f(1))/(3-1)
(1,728-1200)/2
264
The price of a new waverider is $17,000. The sales tax on the waverider is 7.8%. What is the total cost of the waverider including tax?
17,000 X 1.078 = 18,326
$18,326
If
g(x) = 90 *(1/2)^x
what can we say about the "a" value of f? Explain how you know.
The a value of f must be less than 90 because f has a lower y-intercept that g OR because f starts lower on the y-axis
The graph above shows the growth in a rabbit population over time. What is the growth factor? Show or explain your work.
sqrt(20000/200) =10
Write the exponential equation represented by this graph:
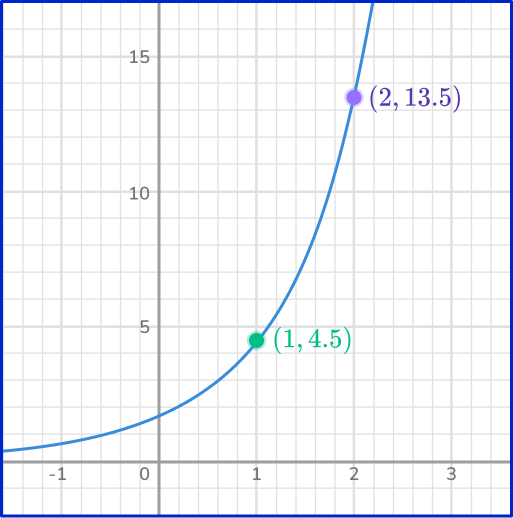
Show or explain your reasoning.
y = 1.5*3^x
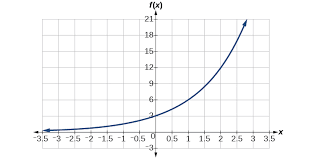
The following graph represents the function f(x)
Using the graph, find f (3). Show or explain your work.
Use the equation
f(x) = 3 *2^x
3 *2^3 = 24
(20,000 x 1.08) x 1.05 = 22,680
