4x + 2 = 14
Determine the slope of the graph
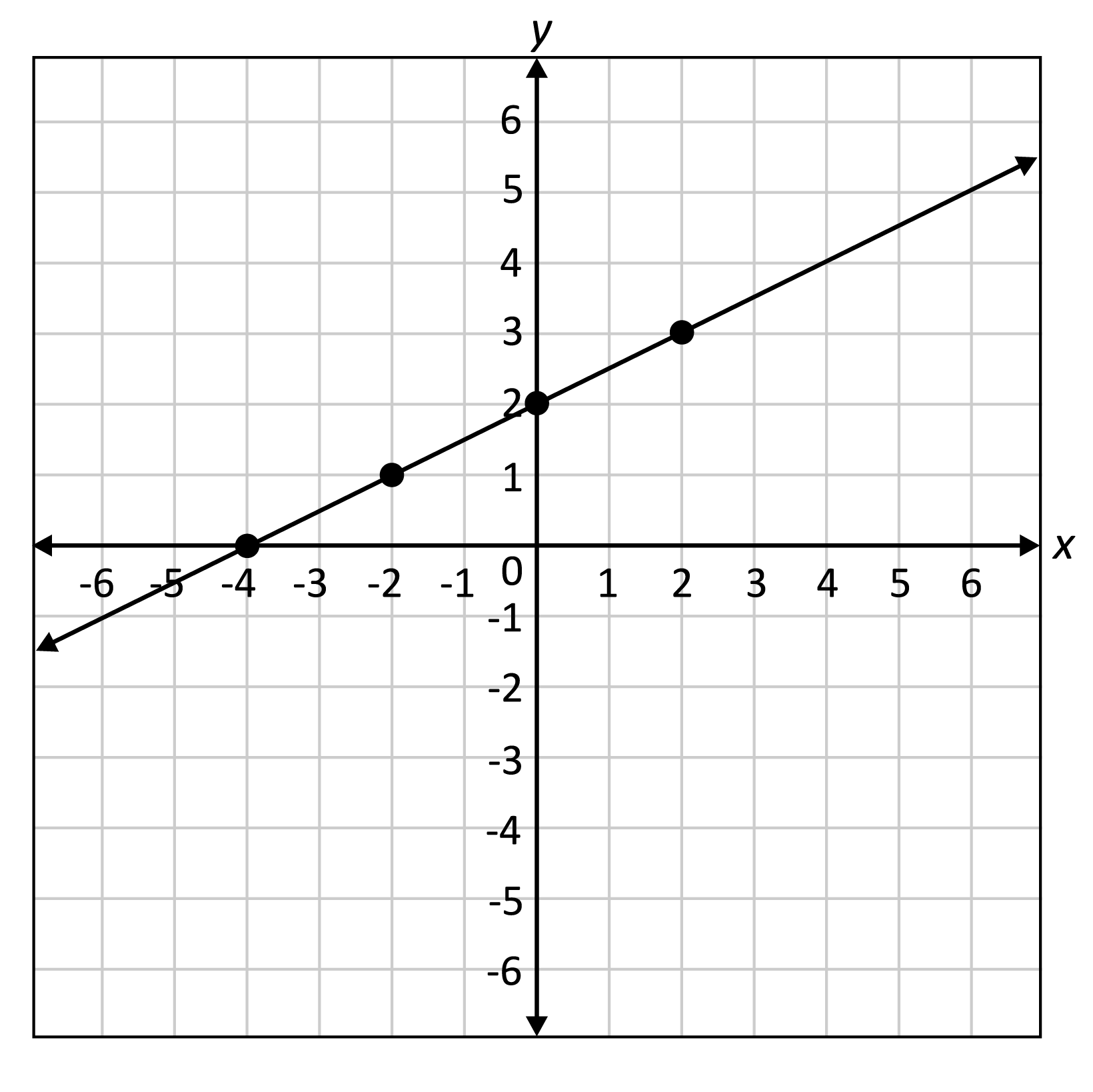
m = 1/2
Determine if the point (1, 2) is a solution to the system of equations:
x + y = 3
x - y = -1
Show your method for credit!
Yes!
1+ 2 = 3
1 - 2 = -1
Determine the vertex AND axis of symmetry of the quadratic :
Y = (x - 5)^2 + 7
Vertex: (5, 7)
AoS: x = 5
Factor the Quadratic below:
Y = x^2 + 5x + 6
y = (x+3)(x+2)
2(x-4) = 10
x = 9
Determine the slope and y-intercept of the equation
Y = (-3/2)x + 10
slope = -3/2
y-intercept = (0, 10)
Find the solution to the system of equations:
Y = 2x + 4
Y = 4x
(2, 8)
Determine the x and y intercepts of the equation below:
Y = (x-3)(x+1)
x-intercepts:
(3, 0) and (-1, 0)
Y-intercept:
(0, -3)
Factor the following Quadratic:
Y = x^2 - 7x - 18
y = (x - 9)(x + 2)
6x + 12 = 4x - 8
x = -10
Determine the equation for the graph below:
y = (-2/3)x + 5
Given the system of equations:
4x - 6 = 3y
x - 1 = y
If you were to use the Elimination Method to solve this system, explain how and where you could multiply by a value, so that adding the equations together would ELIMINATE the term with x.
Multiply the bottom equation by -4, so that adding the equations together would cancel out the x term, leaving you with an easy to solve equation.
Y = (x - 4)(x+2)
y = x^2 - 2x -8
Complete the square for the quadratic Equation, and write the solution in vertex form.
0 = x^2 + 6x + 4
0 = (x+3)^2 - 5
-6x + 10 > -50
x < 10
Re-write the equation below into standard linear form, and determine the slope and y-intercept of the line that would be graphed by the equation:
4Y - 12 = 2Y + 7x -4
M = 7/2
y-intercept = (0, 8)
If you were to solve the following system of equation by substitution:
2y = 8x - 10
2x + 4y = -2
Explain and show how you would isolate a variable in one of the equations, and then use substitution to solve for one of the variables.
Isolate the y in the first equation like so:
y = 4x - 5
Then substitute it into the second equation:
2x + 4(4x-5) = -2
Which solves to get you x = 1
Write the following quadratic equation in standard form
Y = (x-4)^2 + 1
y = x^2 - 8x + 17
Factor the following quadratic:
y=3x^2 - 5x + 2
(3x-2)(x-1)
40 > 2x - 4 > 20
12 < x < 22
Determine a linear equation that would have the following three points as solutions:
(-2, 7)
(-4, 11)
(-6, 15)
y = -2x + 3
Use any method to solve the following system of equations:
y = (5/3)x + 8
-2x = (1/2)y - 21
(6, 18)
Create a quadratic equation that has zeros at x = 2 and x = 6, along with a vertex at (4,-8)
y=2(x-2)(x-6)
y= 4x^2 + 12x - 10
solve it out!