To "flip" a figure.
Reflection
True or False? Dilations always make a figure smaller.
False
Is a dilation of 1.5 an enlargement or reduction?
Enlargement (Gets bigger)
Draw an example of similar squares. Side lengths MUST be included!
When is our first quiz for Unit 2: Dilations?
TOMORROW!!!
To "slide" a figure.
Translation
A dilation might change the size of a figure's side lengths but never the _______.
angles
What transformations can be used to prove similarity.
List them all!
1) Translations
2) Rotations
3) Reflections
4) Dilations
These two triangles are similar. Find the Value of a/b, if the scale factor is 2.
a = 2.8
b = 4.2
The sum of all interior angles in a triangle will always equal this number.
180^o
To "turn" a figure.
Rotation
Dilations always produce ___________ figures.
similar
If the scale factor is greater than 1 (ex:2) then the dilated image is ______________ from the original figure.
Enlarged
Congruent figures are _____ similar.
(sometimes, always)
always
Similar or not similar?
Not similar - angles are not the same.
Describing a rotation requires these three things.
1) Center (Point)
2) Rotation angle (Degrees)
3) Direction (Clockwise or Counterclockwise)
Dilations need these two things.
1) Center Point of Dilation
2) Scale Factor
If the scale factor is less than 1 (ex:1/4) then the dilated image is ____________ from the original figure.
Reduced
Similar figures are ____ congruent.
(sometimes, always)
sometimes
Find the scale factor. Figure EFGH is the original.
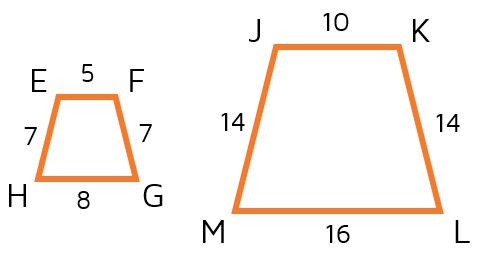
Scale factor = 2
2. The scale factor
3. The coordinates of the center
How will dilating a figure with a scale factor of 1/3 change a figure? How many times bigger or smaller will it get?
It will make the figure 3 times smaller from the center of dilation.
Dilations can result in a congruent figure if their scale factor is this number.
1
These two triangles are similar. Find the missing side lengths.
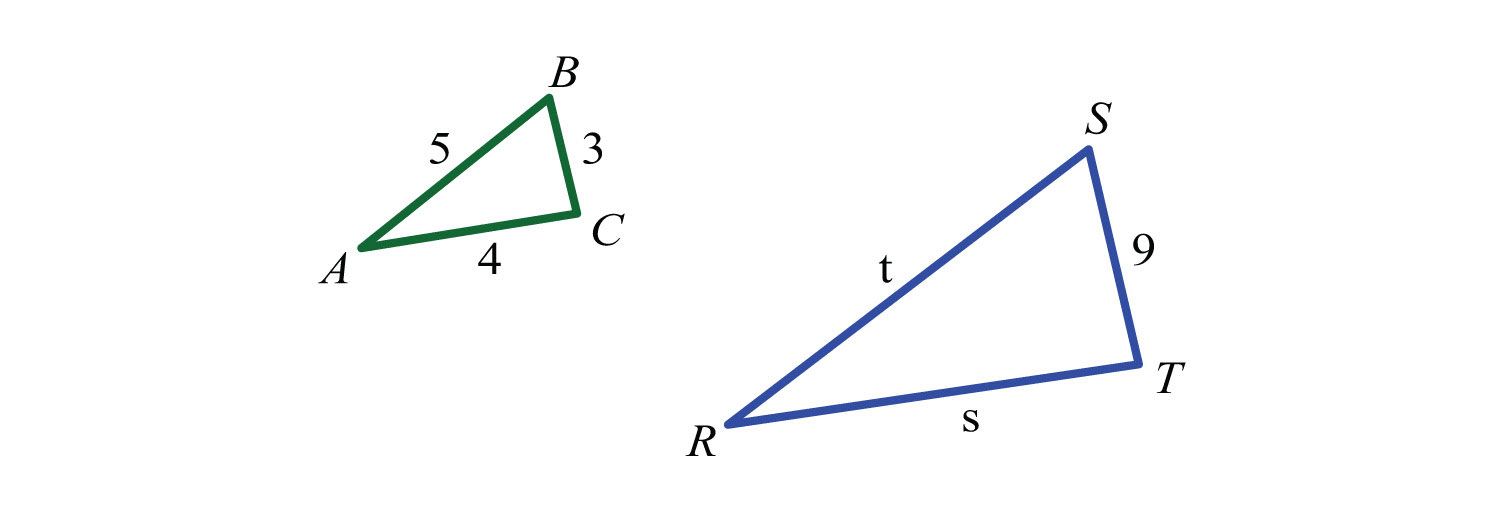
s=12
t=15
What is the value of X and Y when the scale factor is 1/4?

Y= 9 (36x1/4) or (36/4)
What is the scale factor of this dilation: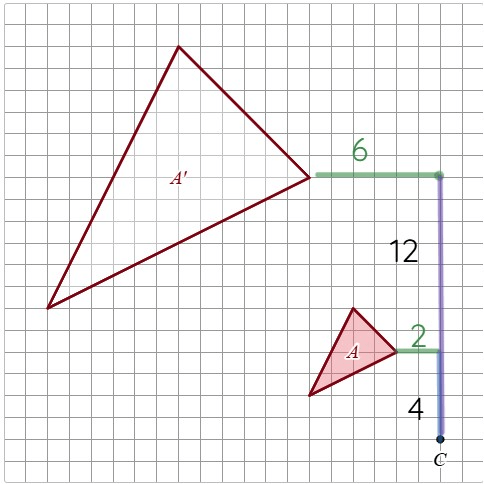
3
Describe this dilation: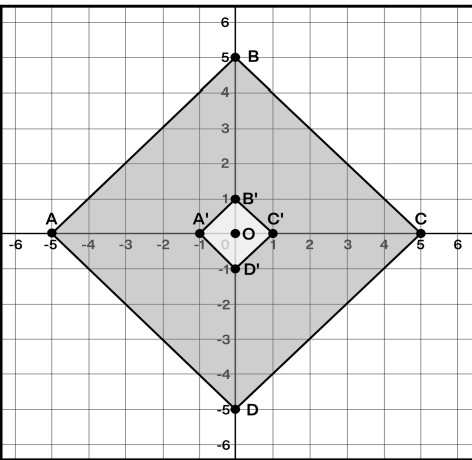
This is a reduction. The center of dilation is (0,0) and the scale factor is 1/5. *Double points for naming the original coordinate points!*
Describe this dilation:
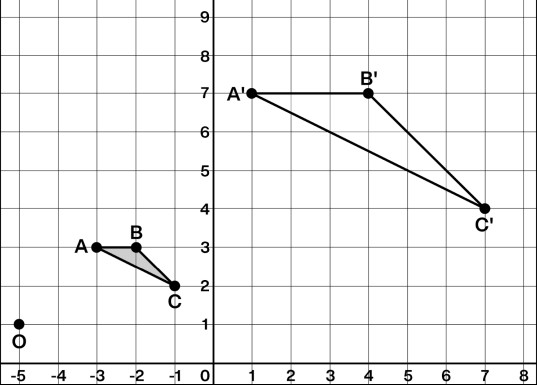
This is an enlargement. The center is at (-5, 1) and the scale factor is 3. *Double points for naming the vertices!*
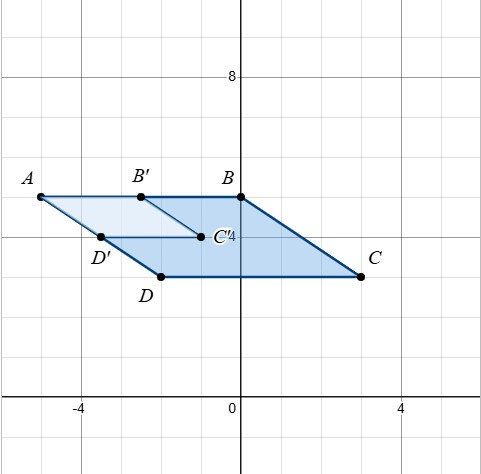 What is the scale factor for this reduction?
What is the scale factor for this reduction?
Are honey possums, possums? ...And do they eat honey?
No! They aren't possums and they don't eat honey. They are DELIGHTFULLY ADORABLE THOUGH!! 

