Identify the domain in inequality notation. 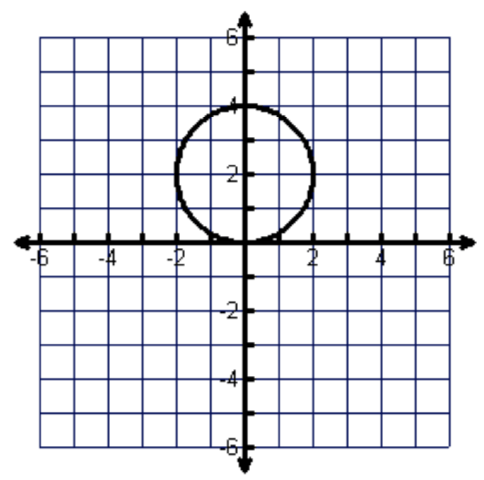
-2 ≤ x ≤ 2
Identify the range in interval notation. 
[-2,-2]
Function? Yes or no? Explain.
NO. Fails the VLT
Write all the intervals of Increasing and Decreasing.
Increasing: -Infinity<x<2
Decreasing: 2<x< Infinity
Write the shift from the parent function and the new pattern.
f(x) = 2(x-3)^2+4
Shift- 3 units right and 4 units up.
New Pattern- 2/1 and 6/1
Identify the domain in interval notation. 
(-4,∞)
Identify the range in interval notation. 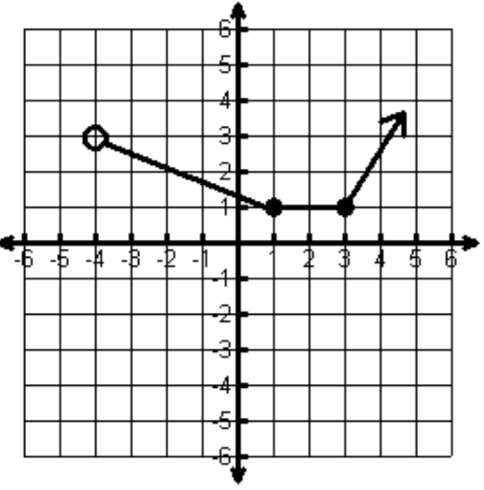
[1,∞)
Function? YES OR NO? 
NO. The inputs of 20 and 22 have more than 1 output
Write all the intervals of Increasing and Decreasing.
Increasing: 3<x< Infinity
Decreasing: -Infinity<x<3
Write the shift from the parent function and the new pattern:
f(x) = -2|x+3|-2
Shift- 3 units left and 2 units down
New Pattern- -2/1 and -2/1
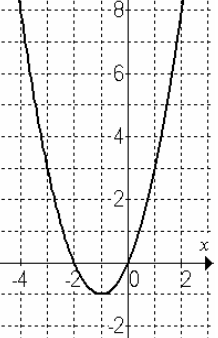
Identify the domain. 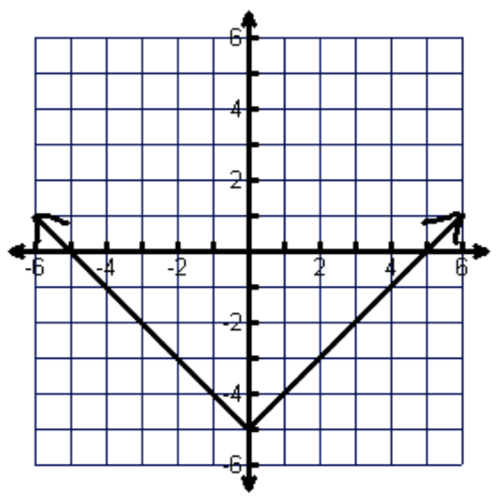
All Real Numbers
Identify the range in inequality notation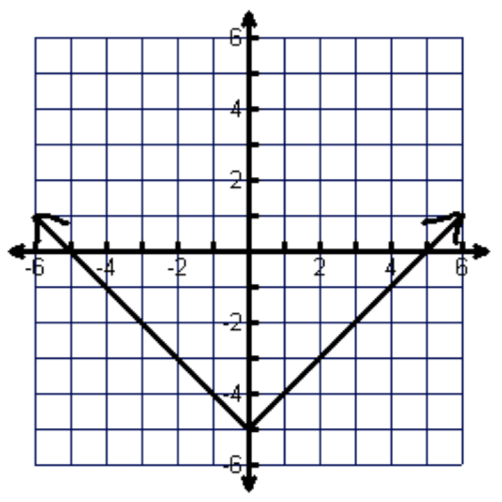
y≥-5
EXPLAIN. Why is this graph a function? 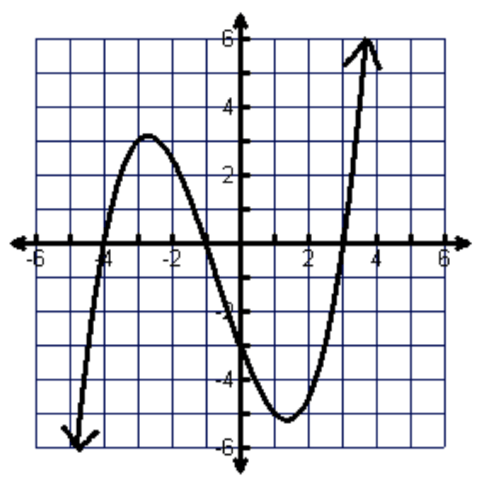
Every input has one output. It passes the vertical line test.
Write all the intervals of Increasing and Decreasing
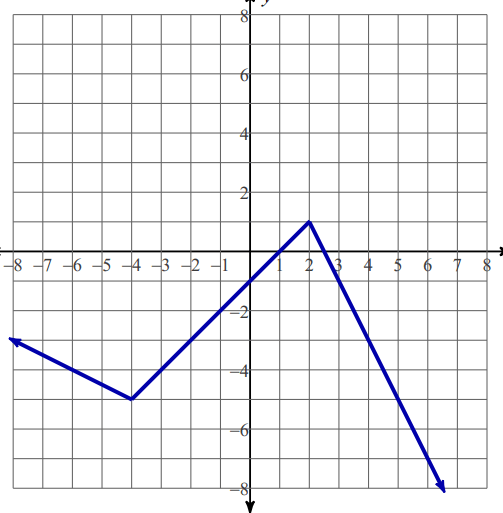
Decreasing: -infinity < x< -4 and 2<x<infinity
Increasing: -4<x<2
Write the shift from the parent function and the new pattern.
f(x) = -3\sqrt(x+1)+3
Shift- 1 unit left and 3 units up.
New Pattern- -3/1 and -3/3
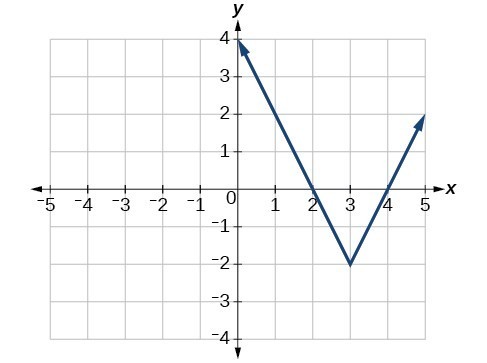
Identify the domain in inequality notation.
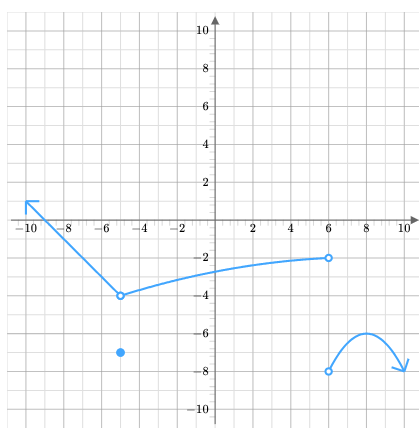
-00 < x <6
6<x<00
Identify the range in inequality notation.
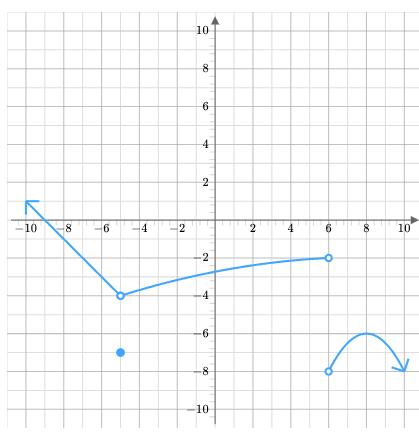
-4 <y<∞
-∞<y<=-6
You draw a vertical line through a graph and it hits 3 times. Is it a function? Explain your response.
No, it can only hit once to be a function
Write all the intervals of Increasing and Decreasing.
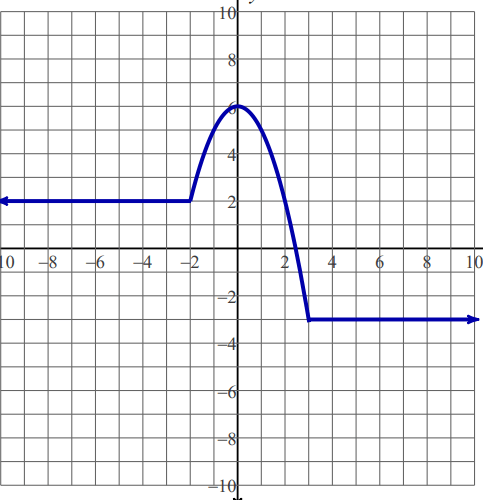
Increasing: -2<x<0
Decreasing: 0<x<3
Based on the graph find the shift from the parent function and new Pattern.
Shift- 1 unit left and 1 unit down.
Identify the domain in inequality notation.
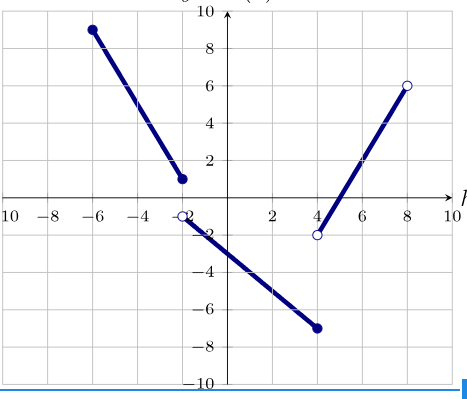
-6 <=x<8
Identify the range.
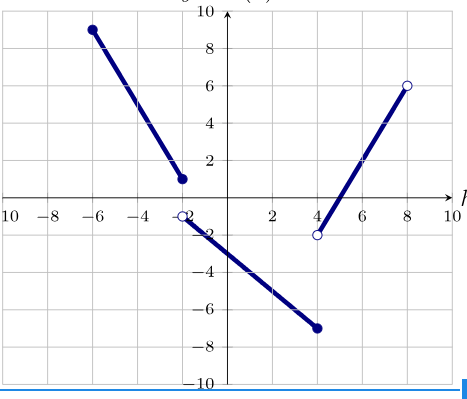
-7 <= x<=9
Name one value of n that would make this NOT a function:
{(2,4), (3,5), (4,-6), (n,7)
2,3,4
Write all the intervals of Increasing and Decreasing.
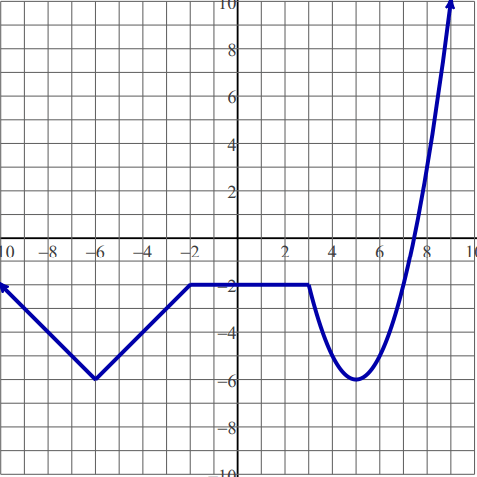
Increasing: -6<x<-2 and 5<x<Infinity
Decreasing: -infinity<x<-6 and 3<x<5
Based on the following graph write the shift from the parent function and the new pattern.
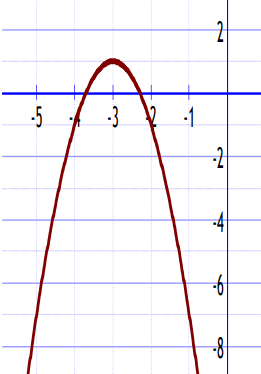
Shift- 3 units left and 1 unit up.
New Pattern- -2/1 and -6/1