Τριγωνομετρικοί αριθμοί γωνίας
Βασικές τριγωνομετρικές ταυτότητες
Αναγωγή στο 1ο τεταρτημόριο
Τριγωνομετρικές συναρτήσεις
100
Μια επίκεντρο γωνία βαίνει σε τόξο S=6cm . Η γωνία αυτή σε ακτίνια, αν η ακτίνα του κύκλου ειναι ρ=2cm είναι:
a=3rad
100
Σωστό ή Λάθος:
Ισχύει σύγχρονως ότι ημx=frac{3}{5} και συνx= \frac{4}{5}
Σωστό
100
συν ( \frac{2 \pi}{3})=
-\frac{1}{2}
100
Η f(x)=2ημ(\frac{\pi}{2}x) έχει ελάχιστη τιμή ... και περίοδο ...
-2, 4
200
H γωνία 1260^ο σε rad είναι:
7π \ rad
200
Να μετατρέψετε την παράσταση ώστε να περιέχει μόνο το συνα:
συν^4α-ημ^4α=
2συν^2α-1
200
Αν συν(\frac{\pi}{2}+x)-ημx=0 , τότε το ημx=
0
200
Η συνάρτηση f(x)=1-2ημx έχει μέγιστη τιμή
3
300
H συνεφαπτομένη της γωνίας 2940^ο είναι
\frac{\sqrt{3}}{3}
300
Να μετατρέψετε την παράσταση ώστε να περιέχει μόνο εφαπτομένες:
\frac{εφα+σφβ}{εφβ+σφα}=
\frac{εφα}{εφβ}
300
Σε κάθε τρίγωνο ΑΒΓ ισχύει ότι ημΑ=
ημ(Β+Γ)
300
Τα κοινά σημεία της συνάρτησης f(x)=1-2συνx με την ευθεία y=2 στο διάστημα (\frac{\pi}{2},\pi) είναι
120^ο\ ή \ \frac{2\pi}{3}
400
Αν ω=15^ο τότε συν (30^ο+ω) είναι:
\frac{\sqrt2}{2}
400
Αν ημx+συνx=α τότε η τιμή της παράστασης ημx \cdot συνx ως συνάρτηση του α είναι:
\frac{α^2-1}{2}
400
ημ^2(\pi-x)+συν(\pi-x)συν(2\pi-x)+2ημ^2(\frac{\pi}{2}-x)=
1
400
Η εξίσωση της συνάρτησης της παρακάτω γραφικής παράστασης είναι:
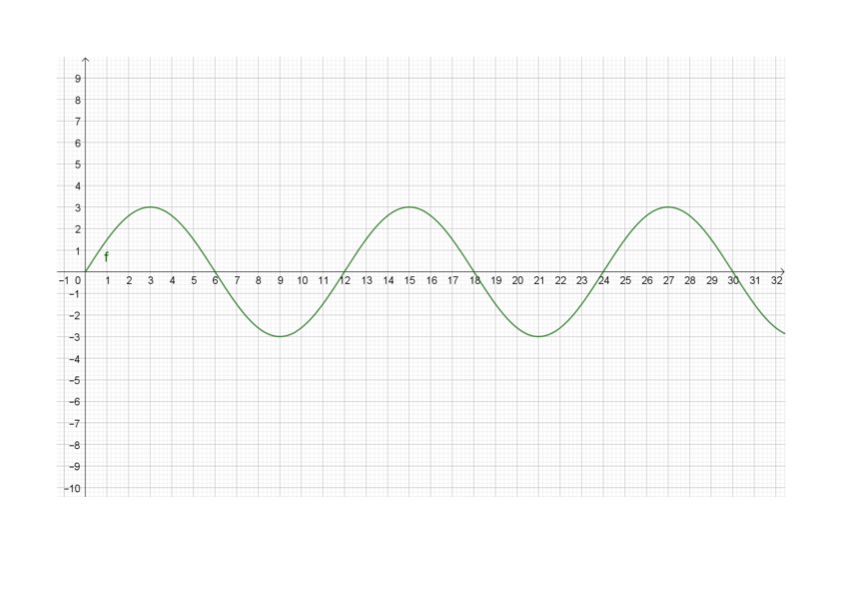
f(t)=3ημ(\frac{\pi]{6}t)