Hashing
Search Trees
Graphs
Algorithm Families
Dynamic Programming
100
This collision resolution scheme supports more data than there are available buckets.
Separate Chaining
100
Describe the differences in space requirements for array-based binary trees and complete binary trees.
Binary tree:
O(2^n)
Complete binary tree:
O(n)
Complete binary tree: All layers (except possibly the last) are full, and all leaves are either: (1) at the maximum depth, d, and as far left as possible OR (2) to the right of all internal nodes at depth d-1.
100
This is the difference between sparse and dense graphs.
Sparse: |E|<<|V|^2
Dense: |E| ~~ |V|^2
100
Describe some differences between Backtracking and Branch and Bound.
Backtracking: constraint satisfaction; stop when a solution is found
Branch and bound: optimization; estimate partial solutions; run until everything is tested and return the best
100
How does bottom-up dynamic programming differ from top-down?
Bottom-up is typically iterative while top-down is typically recursive. Bottom-up starts with the smallest problem instance and builds up larger instances.
200
For open addressing, this happens when the load factor reaches a pre-determined threshold.
The underlying array is resized (often doubled) and all previous elements are rehashed and inserted.
200
What data structure is used for processing nodes in a breadth-first (level-order) traversal of a tree? A depth-first traversal?
BFS: queue
DFS: stack
200
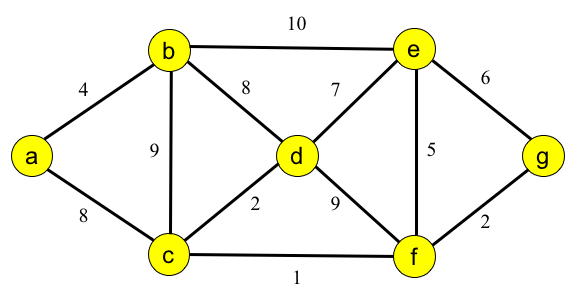
Provide the order of edges being added to the MST (starting at A) using Prim's on the following graph.
(a,b), (a, c), (c, f), [(c, d) (f, g)], (f, e)
OR
(a, b), (b, d), (d, c), (c, f), (f, g), (f, e)
200
A greedy algorithm will always find an optimal solution for this version of the Knapsack problem.
Fractional Knapsack
200
Describe the modifications needed for a recursive function to make use of memoization.
At function entry, look up the input. If there is an answer, return it. Otherwise, run the function.
At function exit (return), store the input, output pair*
* this may not be an actual pair: use an appropriate data structure
300
Double Hashing, while often slower than some other open addressing schemes, can improve overall performance by reducing these in a hash table.
What are clusters?
300
In a BST, what is swapped with the node to be removed?
The inorder predecessor or inorder successor
300
Provide the order of edges being added to the MST (starting at A) using Kruskel's on the following graph.
(c, f), [(c, d), (f, g)], (a, b), (f, e), [(a, c) OR (b, d)]
300
This algorithmic approach can be used to find a graph coloring solution more quickly* than brute force.
* most of the time
Backtracking
300
Implemented naively, will a bottom-up or a top-down solution to a problem perform less work?
For naive implementations, top-down solutions can perform less work (they will only compute answers for subproblems that are needed in the final solution).
400
The complexity of inserting into a hash table with m slots that stores n unique keys.
- Separate chaining (best, worst, avg)
- Linear probing (best, worst, avg)
- Separate chaining
- Best, worst, average
- O(1), O(n), O(n/m) ≈ O(1)
- Linear probing
- Best, worst, average
- O(1), O(n), O(n/m) ≈ O(1)
400
What is the worst-case time complexity for search/insert in an AVL tree? BST?
AVL: log(n)
BST: n
400
This data structure is used to make Kruskal's algorithm efficient.
Union-Find (with path compression...and rank!)
400
This algorithmic technique BEST describes the following code.
Brute Force (divide and conquer is tempting, but the subproblems are not independent)
400
Briefly describe solving 0-1 Knapsack with a bottom-up dynamic programming solution
Start at backpacks of size 0, go up to size M.
Compute the maximum value for backpacks of size k as follows:
For each item with (size, value), compute "max value for backpack k - size" + value; take the largest of these.
500
Assume the hashing function is just "mod 8". Where will 14 be inserted with linear probing and quadratic probing? Which is better?
Linear: 1
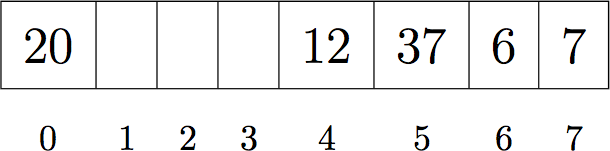
Quadratic: 2
Quadratic requires fewer probes
500
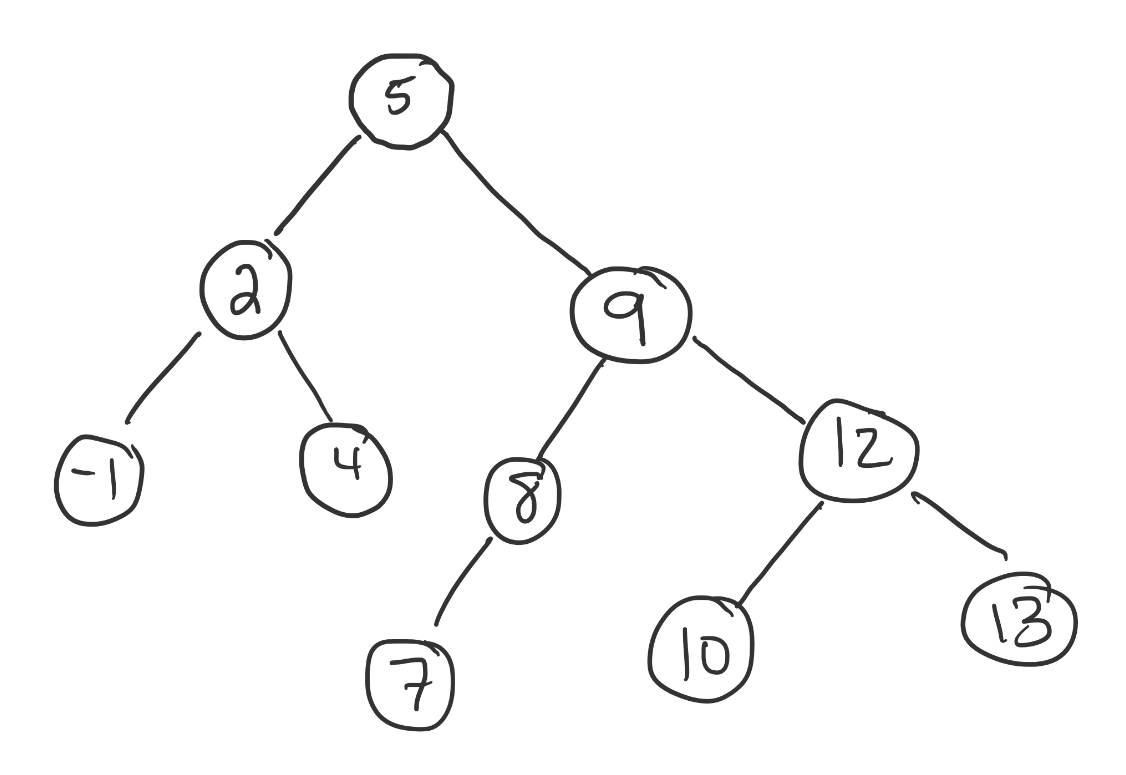
The AVL tree after inserting
4, 2, -1, 5, 7, 8, 9, 13, 12, 10
500
Give the shortest path from "a" to all other vertices in the following graph.
b: 4, c: 8, d: 10, e: 14, f: 9, g: 11
500
Give a set of coin denominations and change amount for which a greedy change algorithm will NOT work.
There are many examples. One is:
12 cents: 1 cent, 6 cent, 10 cent500
Given two strings str1 and str2 and below operations that can performed on str1. Find minimum number of edits (operations) required to convert ‘str1’ into ‘str2’.
Operations: Insert, Remove, Replace
All of the above operations are of equal cost.