Properties of Parallel Lines
Congruent Triangles
Similar Triangles
Scale Factor
Pythagoras
100
Solve for a and b
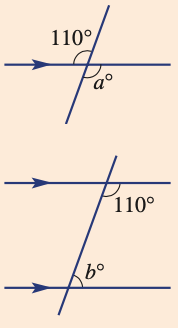
a = 110° (vertically opposite)
b = 70° (co-interior angles)
100
Which congruence test would be used to show that these pairs of triangles are congruent?
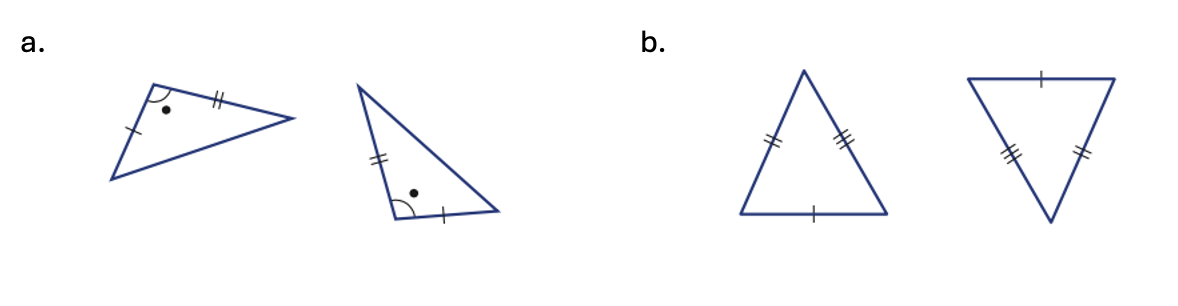
a. SAS
b. SSS
100
What similarity test would you choose to prove that these two triangles are similar? Why?
SSS - all three sides have the same scale factor
100
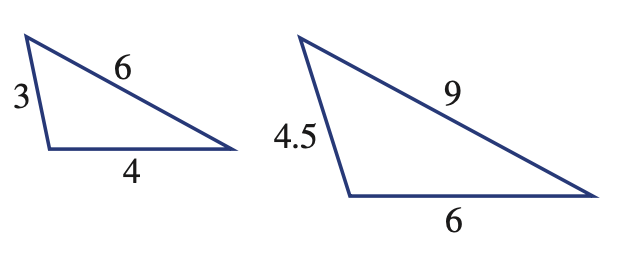
What are the scale factors for the following pairs of similar triangles?
a.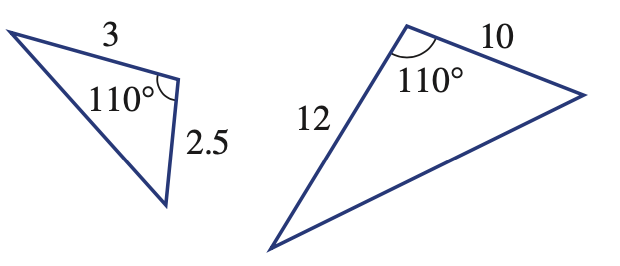
b.
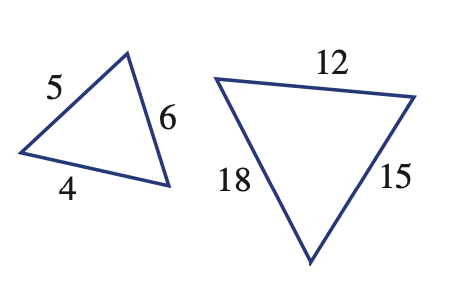
a. 4
b. 3
100
Find b and c
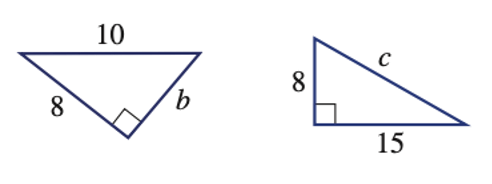
b = 6
c = 17
200
Find angle z and t
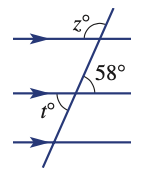
z = 58° (alternate)
t = 58° (vertically opposite)
200
Which two triangles are congruent and which test would you use?
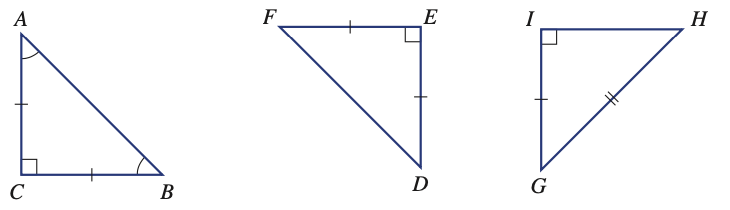
△ABC ≡ △DFE (SAS)
200
Determine if the following pairs of triangles are similar, and state the similarity test which proves this.
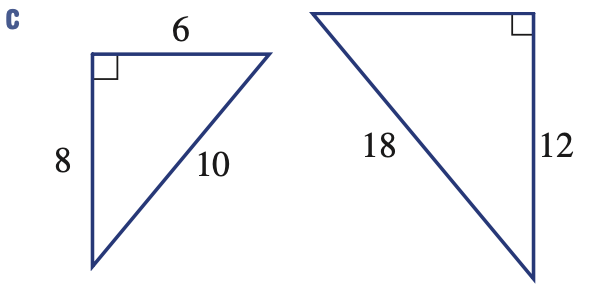
a. Similar - SAS
b. Similar - AAA
c. Not Similar - sides don't have the same scale factor
200
a. Find the scale factor for these similar triangles.
b. solve for x only
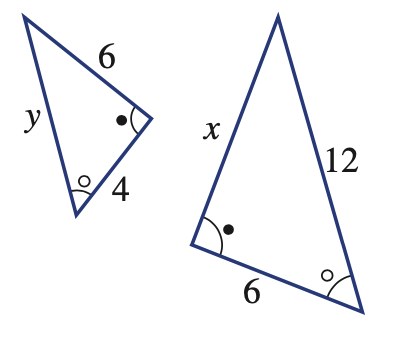
a. scale factor is 1.5
b. 9
200
Find the perimeter of this triangle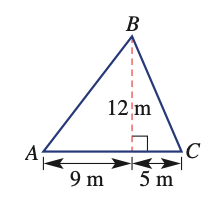
P = 42m
*find BC and AB
300
Sove for x
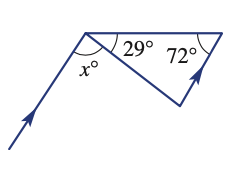
x = 79°
**x+29 is co-interior with 72°
300
If these two triangles are congruent, solve for x, y and a
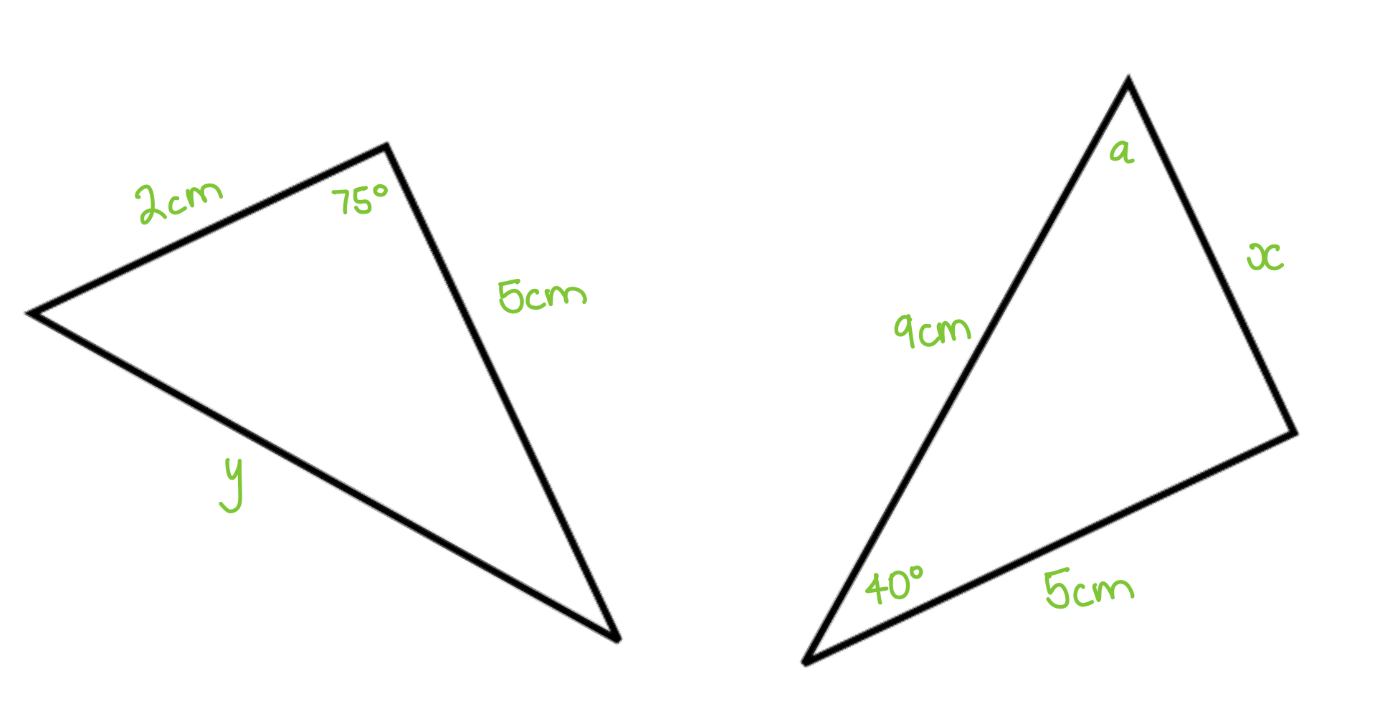
x = 2cm
y = 9cm
a = 65°
300
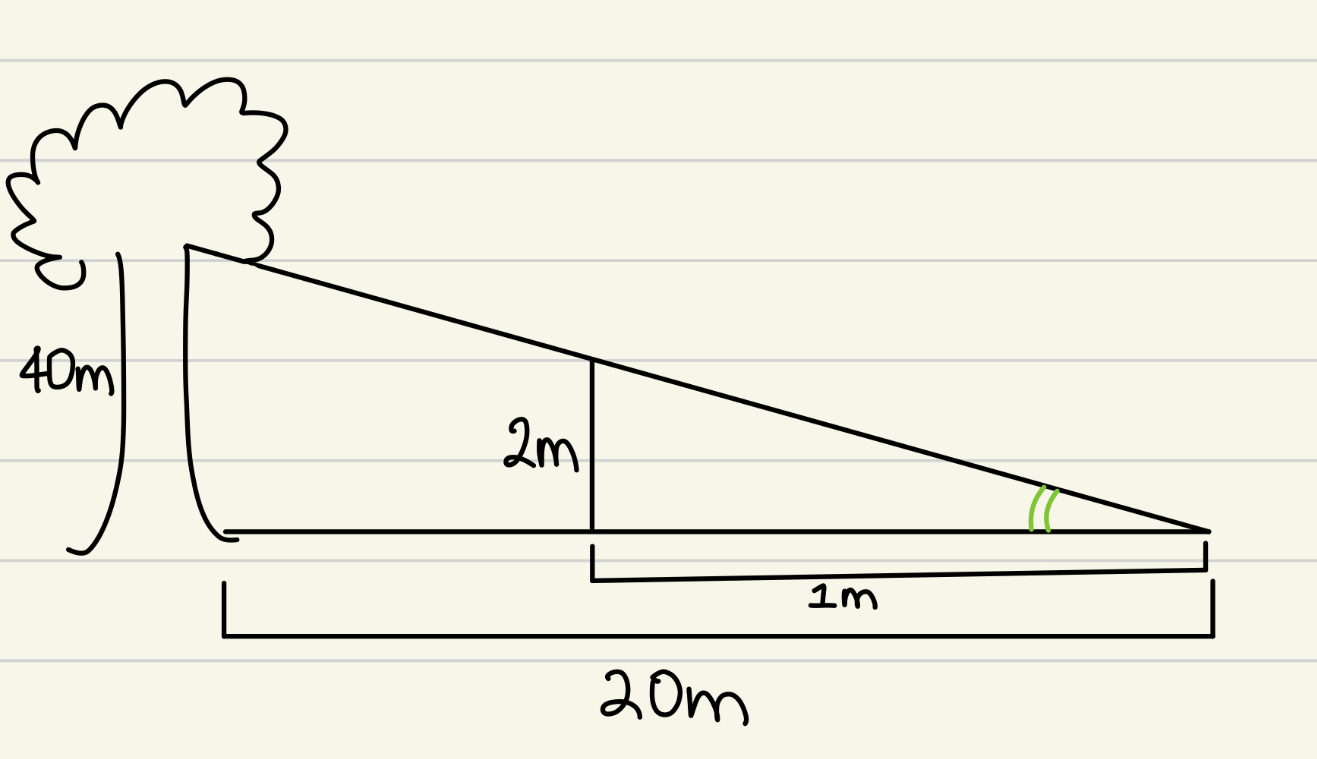
A tree’s shadow is 20m long, while a 2m vertical stick has a shadow 1m long. The tree is 40m tall. What proof would you use to prove these two triangles are similar?
SAS
300
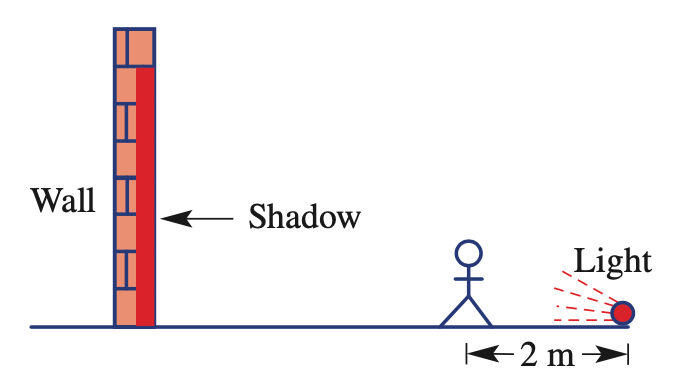
A person 1.8 m tall stands in front of a light that sits on the floor, and casts a shadow on the wall behind them. How tall will the shadow be if the distance between the wall and the light is 10m?
9 meters
300
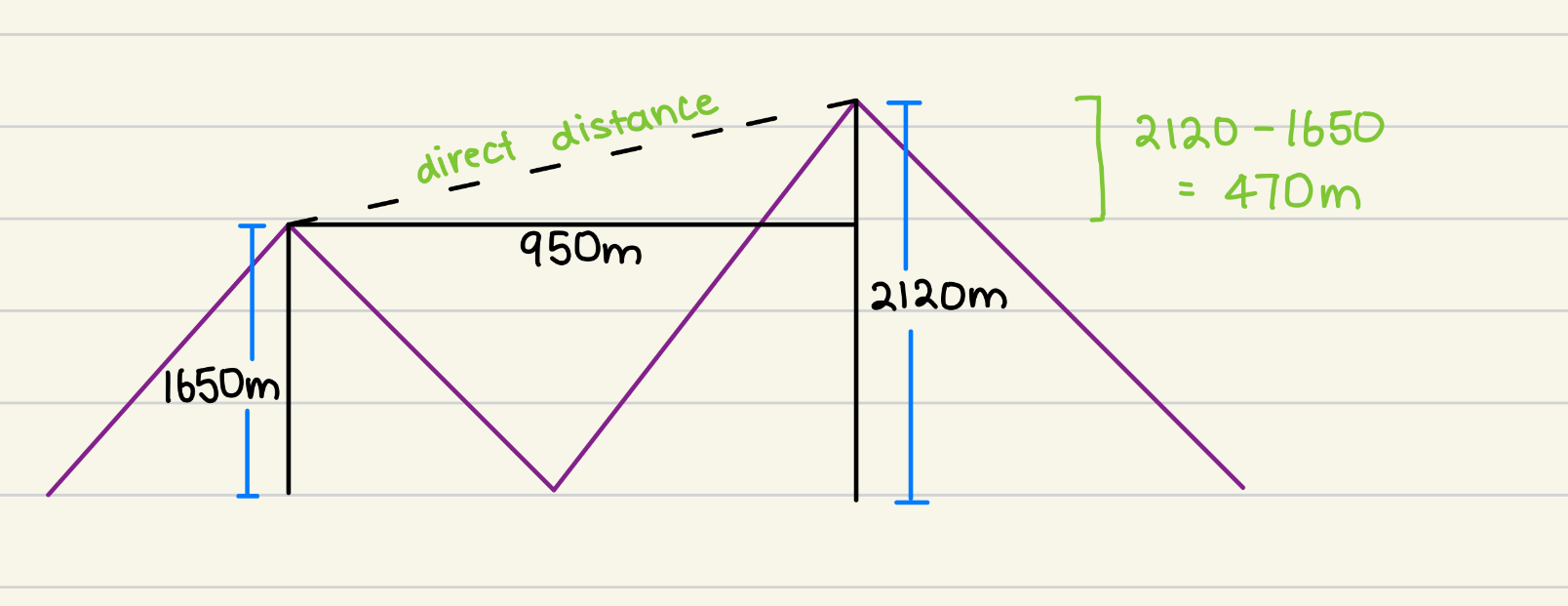
Two bushwalkers are standing on different mountain sides. According to their maps, one of them is at a height of 2120 m and the other is at a height of 1650 m. If the horizontal distance between them is 950 m, find the direct distance between the two bushwalkers. Give your answer correct to the nearest metre.
1060m
400
Find the value of x
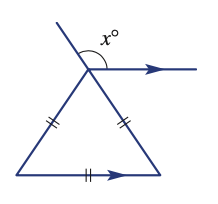
x = 120°
**equilateral triangle - all angles are the same
400
Prove that these two triangles are congruent
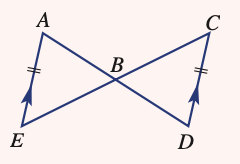
1. AE = CD (given)
2. ∠EAB = ∠CDB (alternate angles)
3. ∠ABE = ∠EBD (vertically opposite)
∴ △ABE ≡ △DBC (AAS)
400
Which two triangles are similar? Write a similarity statement to proof that they are similar.
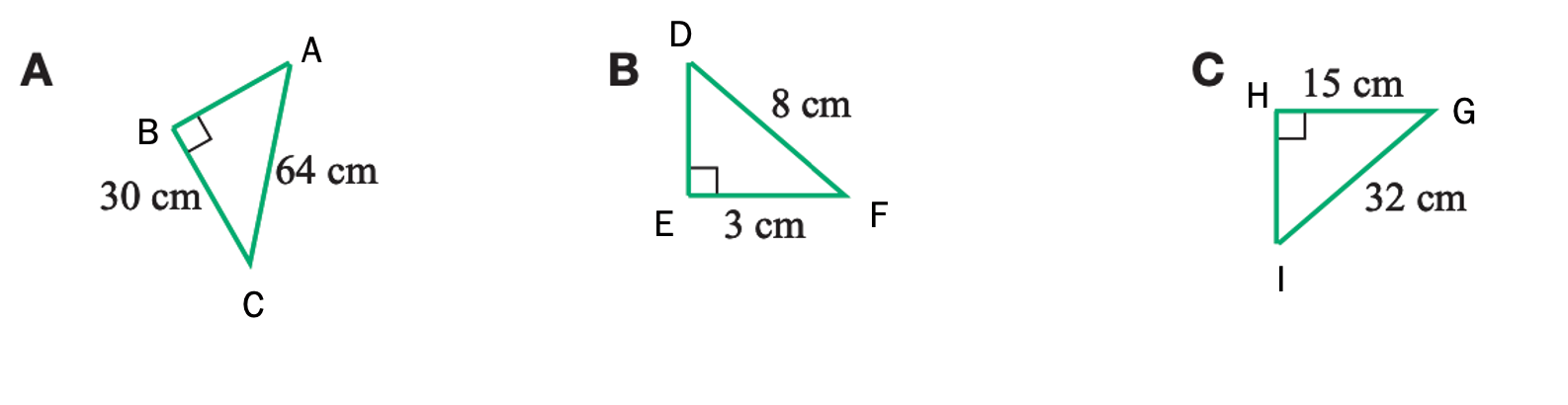
A & C
1. AC ∝ GI (same scale factor)
2. BC ∝ HG (same scale factor
3. ∠ABC = ∠IHG (given)
∴ △ABE ≡ △IHG (SAS)
400
These two triangles are similar. Find AB:
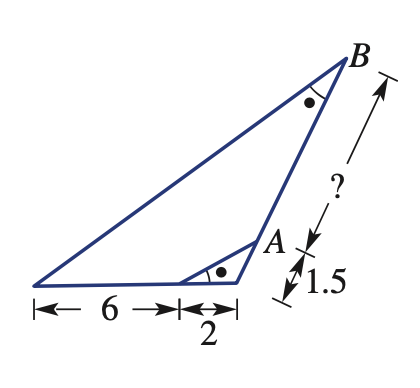
AB = 4.5
**S.F = 1/4
400
Find the height (h) of the dog kennel in meters
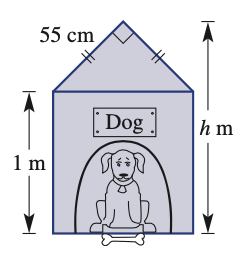
h = 1.39m
*use simultaneous equations