Determining the Number of Solutions
Solving Equations Graphically
Solving by Factoring and the Square Root Principle
Applying the Quadratic Equation
Inequalities
100
b^2-4ac
What is the formula for the discriminant?
Explanation: The discriminant is a formula used to tell the number and types of solutions of a quadratic equation. It is also the formula underneath the radical of the quadratic equation.
100
The solutions to the graph 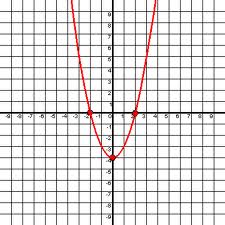

What is -2 and 2?
Explanation: Look at where the graph crosses the x-axis. Wherever the graph intercepts the axis is known as the solutions to the equation. It crosses the axis at 2 and -2, therefore those numbers are the solutions.
100
The solutions to x^2-x-12.
What is 4 and -3?
Explanation: The quadratic equation factors into (x-4)(x+3). If you set each of them to 0, you get x=4 and x=-3
100
The Quadratic Equation
What is 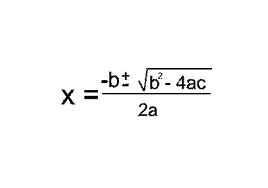 ?
Explanation This equation is used to determine the solutions to a un-factorable quadratic equation or an equation with complex solutions.
?
Explanation This equation is used to determine the solutions to a un-factorable quadratic equation or an equation with complex solutions.
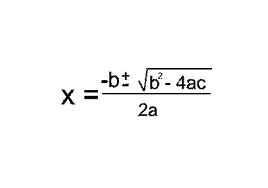 ?
Explanation This equation is used to determine the solutions to a un-factorable quadratic equation or an equation with complex solutions.
?
Explanation This equation is used to determine the solutions to a un-factorable quadratic equation or an equation with complex solutions.100
The range of solutions for x^2+x-6 <0
What is -3 < x < 2 ?
Explanation: Solve the quadratic equation to get x = -3 and 2. Set up a number line and choose test values. All numbers between -3 and 2 make the original inequality true.
200
The number of solutions to -2x^2-6x+10.
What are two real solutions?
Explanation:b^2 - 4ac is the discriminant. It tells you the number and type of solutions to a quadratic equation.If b^2 - 4ac > 0 then the graph must never cross the x-axis two times.
200
The number of solutions to the graph 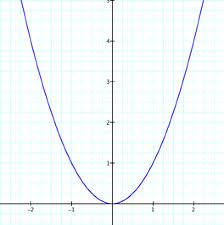

What is 1?
Explanation Look at the graph and determine the number of times it crosses the x-axis. The graph crosses the x-axis once, therefore it only has 1 solution.
200
The solutions to 5x^2+10x+5.
What is -1?
Explanation:You can first factor out a GCF of 5 to get 5(x2 + 2x + 1) = 0, which can be factored into 5(x + 1)(x + 1) = 0.Set the two binomials equal to 0 and solve to get -1.
200
The solutions to 2x^2 + 4X -30 = 0
What is 3 and -5 ?
Explanation: Insert the equation into the quadratic formula. Solve the equation to get -4 ± Sq Root ( 16 + 240 ) / 4. Simplify the equation to determine the roots of 3 and -5.
200
The range of solutions for x^2-x-12 < 0
What is -3 < x < 4 ?
Explanation: First,replace the inequality sign with an equals sign and solve the quadratic equation to get x = -3 and 4. Set up a number line and choose test values. All numbers between -3 and 4 make the original inequality true.
300
The type of solutions to this graph:


What are two complex solutions?
Explanation: If the graph of a Quadratic Equation does not cross the x-axis of the graph at a point, it has no real solutions and two complex solutions.
300
The solutions to 
What is 2 and 3?
Explanation: Look at where the graph crosses the x-axis. Wherever the graph intercepts the axis is known as the solutions to the equation. It crosses the axis at 2 and 3 , therefore those numbers are the solutions.
300
The solutions to 6x^2-10x+2
What is -3/2 and 7 ?
Explanation:The quadratic equation factors into (2x + 3)(x - 7). You can set each factor equal to 0 and solve you get -3/2 and 7. You can also graph the equation and see where the line crosses the x-axis or use the quadratic equation.
300
The solutions to 6x^2-10x+2
What is 5±1 Sq Root(7) / 6 ?
Explanation In order to solve the problem you must apply the quadratic formula. Then apply the quadratic formula to the problem. Simplify the equation to get 5 ± 1 Sq Root ( 7) / 6 .
300
The range of solutions for x^2-7x+11 < 10
What is 1< x < 6?
Explanation:The correct answer is 1 < y < 6. First,replace the inequality sign with an equals sign and solve it to get x = 1 and 6. Set up a number line and choose test values. All numbers between 1 and 6 make the original inequality true.
400
A)b^2 - 4ac > 0
B)b^2 - 4ac = 0
C) b^2 - 4ac < 0
A)What is the discriminant of an equation with 2 distinct real solution?
B)What is the discriminant of an equation with 1 real solution?
C)What is the discriminant of an equation with no solutions?
Explanation There are 3 formulas to determine the amount of solutions an equation has. This equation is determined by the formula under the radical of the quadratics. If the solution determined is >0, it has 2 solutions; if it is 0, it has 1 solution and if it is< 0, then it has NO REAL SOLUTIONS.
400
The solutions to 

What is -3 and 1?
Explanation: Look at where the graph crosses the x-axis. Wherever the graph intercepts the axis is known as the solutions to the equation. It crosses the axis at 3 and -1, therefore those numbers are the solutions.
400
Solution to x^2- 2x+1 =14
What is 1±Sq Root (14)?
Explanation In order to solve this, you must apply the square root principle. First, factor out the left side, and rewrite the equation has (x-1)^2=14. Then take the square root of both sides to get Sq Root(x-1)^2=± Sq Root (14) . Add 1 to both sides to get 1± Sq Root(14)
400
The solutions to x^2+10x+25=7
What is -5 ± Sq Root ( 7) ?
Explanation In order to solve the problem, subtract 7 from both sides to get x^2+10x+18=0. Then apply the quadratic formula to the problem. Simplify the equation to get -5 ± Sq Root ( 7) .
400
The range of solutions for x^2+9x-16
What is x<-11 and x>2 ?
Explanation: First, subtract 6 from both sides of the inequality. Once all the the numbers are on the left side of the < sign, solve like a quadratic equation to determine the solutions. Create a number line with these solutions and use test values between, after and before the solutions to determine the range of solutions.