Consider the sequence:
25,21,17,13,…
Identify the first term and the common difference.
a1=25
d=-4
 A taxi service charges a fixed fee of $8 plus $1.75 for each mile traveled.
A taxi service charges a fixed fee of $8 plus $1.75 for each mile traveled.
Determine the y-intercept.
b=8
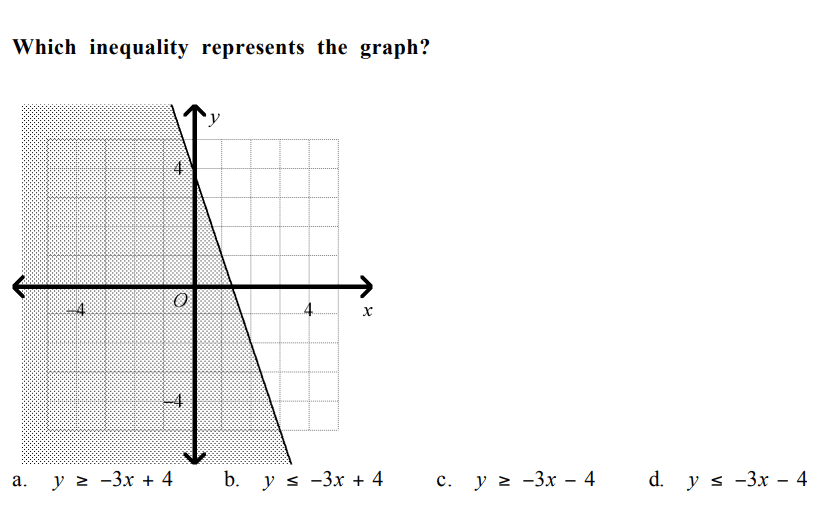
d. y≤-3x-4
Given the graph of the following system of linear inequalities, which region should be shaded?
2x+y<-2
2x-3y≤ -6
4
Determine the slope and y-intercept of the linear function represented by the following scenario:
Brooke and her friends decide to go bowling. The cost for the group is $15 for shoe rentals plus $4.00 per game.
m=4
b=15
Given the sequence:
7,11,15,19,…
Write the explicit formula for the nth term of the sequence.
an=7+4(n−1)
 UPS charges a base fee of $5 plus $2.50 for each package delivered.
UPS charges a base fee of $5 plus $2.50 for each package delivered.
What is the slope?
m=2.50
You're heading to a concert and decide to take a Lyft during peak hours. The Lyft service charges a flat service fee of $15, plus $0.75 per mile traveled. You have a Lyft gift card with at most $50 left on the card.
Before the ride, your friend mentions that Lyft also charges a tip and taxes — but you realize those are already covered separately and don’t come out of the gift card.
Write an inequality that represents this scenario.
15+0.75m≤50
or 50≥15+0.75m
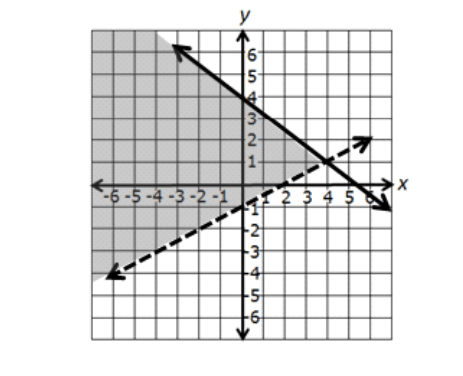
Select the 2 points that are NOT part of the solution set to the system of inequalities shown in the graph.
a.(4,1) b.(-1,-1) c. (-4,1) d.(2,1) e.(0,-3)
b.(-1,-1)
e.(0,-3)
At her job, Pat earns $25,000 the first year and receives a raise of $1000 each year. The explicit formula for the nth term of this sequence is an=25,000+(n-1)1000`.
Write the equivalent recursive formula?
a1=25,000,
an=an-1+1000
Find the next term in the sequence:
4,9,14,19,_
24
A delivery service charges a base fee of $5 plus $2.50 for each package delivered. If the total cost for delivering a certain number of packages is $42.50, determine how many packages were delivered.

15 packages.
A taxi service charges a fixed fee of $8 plus $1.75 for each mile traveled. If the you have at least $25 to spend, determine the number of miles you could travel before running out of money.
9 miles
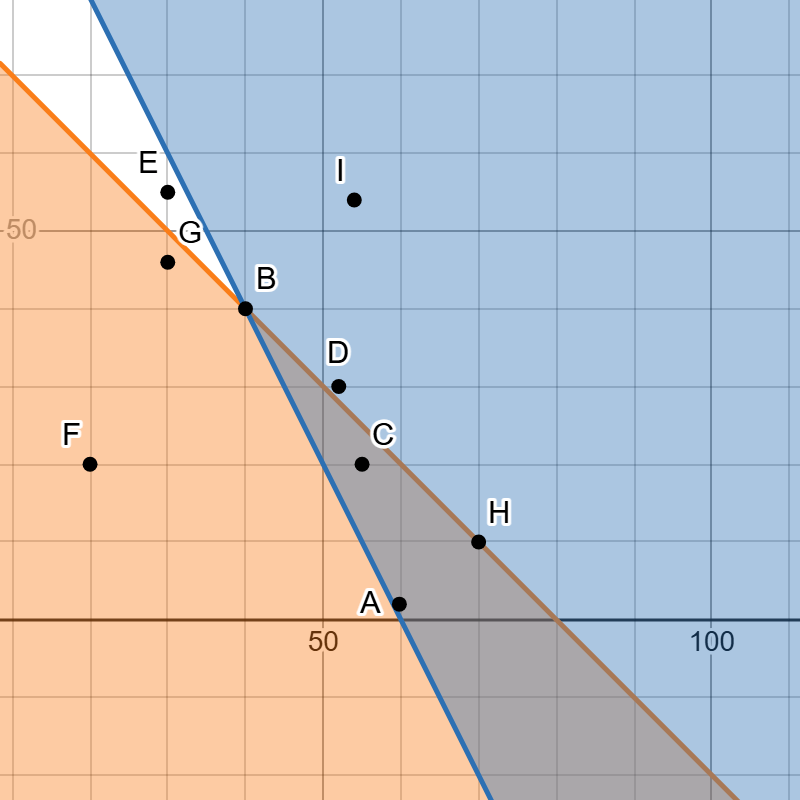
Cullin needs to save at least $100 for homecoming. He works 2 jobs earning $8 per hour at Culvers and $25 per hour mowing lawns. He can only work at most 14 hours before homecoming.
Write a system of inequalities to represent the situation.
x+y≤ 14
8x+25y≥ 100
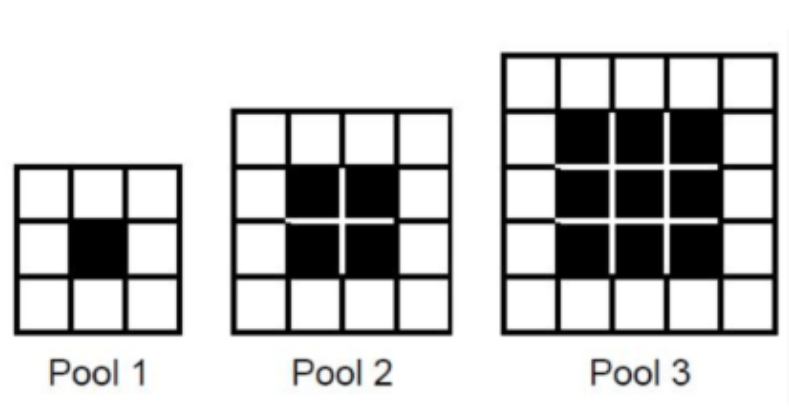 Write an equation to represent the pool pattern. explicit or recursive.
Write an equation to represent the pool pattern. explicit or recursive.
Explicit: an=8+4(n-1)
a1=8
an=an-1+4
Write the recursive formula for the given sequence:
−3, 2,7,12,…
a1=−3
an=an−1+5
Laney's math department is organizing a field trip. The initial number of students signed up is 40, and each week, 9 more students join the trip. If the pattern continues and the math department allows sign up for for 6 more weeks; how many students will attend the trip?

94 students
You're heading to a concert and decide to take a Lyft during peak hours. The Lyft service charges a flat service fee of $15, plus $0.75 per mile traveled. You have a Lyft gift card with at most $50 left on the card.
Before the ride, your friend mentions that Lyft also charges a tip and taxes — but you realize those are already covered separately and don’t come out of the gift card.
Would possible solutions be included on the line? Would possible solutions be above or below the line?
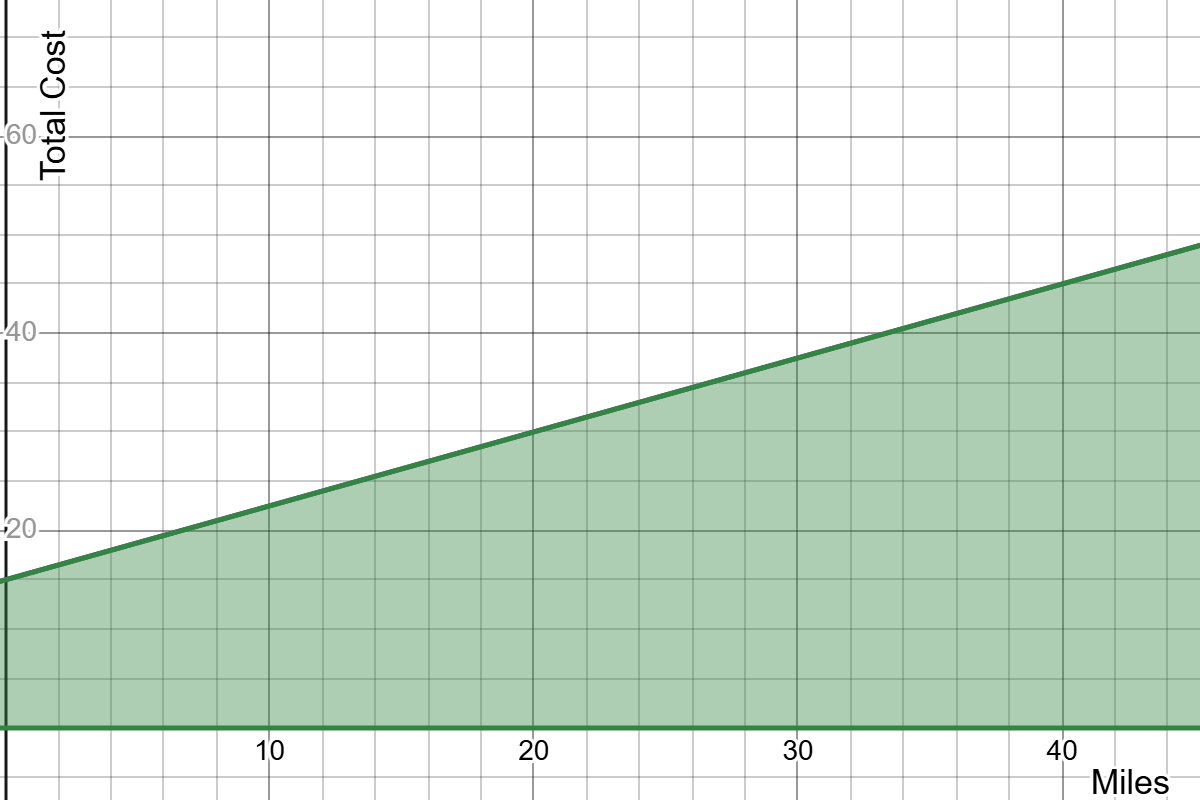
The Laney Pearls are organizing a fundraiser. The entrance fee for adults is $10, and for children, it is $5. Their goal is to collect at least $600. The venue can hold no more than 80 people.
let a = adult tickets and c = child tickets
Which points on the graph are possible solutions?
A, B, C, H
 What is the 5th term in this sequence?
What is the 5th term in this sequence?
11
Find the 8th term in the sequence
Sequence: 5, 3, 1...
-9
Jasmine is saving money to buy a new bicycle. The bike she wants is $275. She already has $50 saved, and she plans to save an additional $15 each week from her part-time job.
Write a linear equation that models this situation in slope intercept form.
y=15x+50
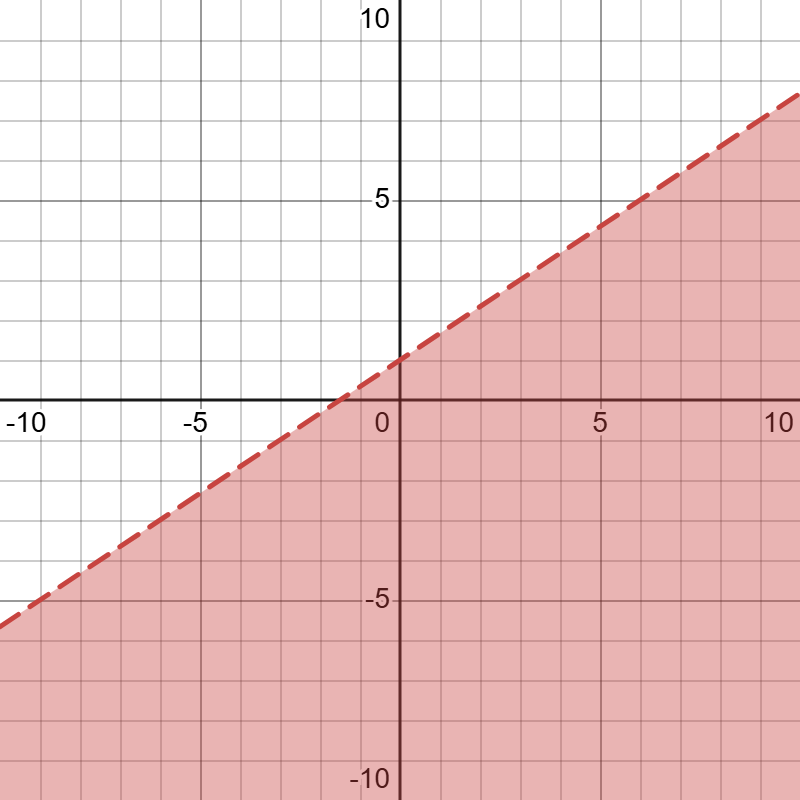 Which points are possible solutions? Tell all that apply.
Which points are possible solutions? Tell all that apply.
a. (0,0) b. (-3,-1) c. (3,3) d. (0,5) e. (5,4)
a. (0,0)
d. (0,5)
e. (5,4)
Cullin needs to save at least $100 for homecoming. He works 2 jobs earning $8 per hour at Culvers and $25 per hour mowing lawns. He can only work at most 14 hours before homecoming.
Which is not a solution?
a. 0 hours at Culvers and 14 hours mowing lawns
b. 1 hour at Culvers and 3 hours mowing lawns
c. 0 hours at Culvers and 4 hours mowing lawns
d. 5 hours at Culvers and 9 hours mowing lawns
e. 14 hours at Culvers and 0 hours mowing lawns
b. 1 hour at Culvers and 3 hours mowing lawns
Is this an arithmetic or geometric sequence? Write the explicit form of the equation that represents this pattern.
Geometric
an=3(4)n-1