Elevation and Depression
Trigonometry
Simultaneous Equations
Equations
Bearing
100
If the elevation of the Sun is 57°, how long a shadow will be cast by a 23.2 m pole? Round your answer to one decimal place.
15.1 m
(Draw a diagram.For the 57° angle, the pole is the opposite side, and the shadow is the adjacent side.)
100
24 In the right-angled triangle below, AB = 20 cm, BC = 12 cm and AC = 16 cm. Express tan B as a ratio in simplest form. (Note the diagram is not drawn to scale.)
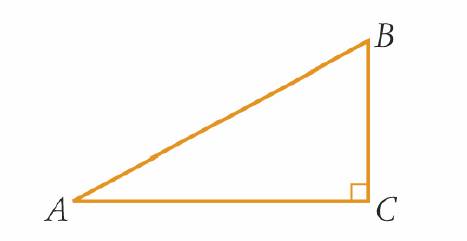
4/3
100
On the same axes, sketch the graphs of 2x + y = 6 and x – y = 9. Use your graph to solve the simultaneous linear equations
x = 5, y = –4
100
Draw the graph of the equation x = –2
a vertical line through (–2, 0)
100
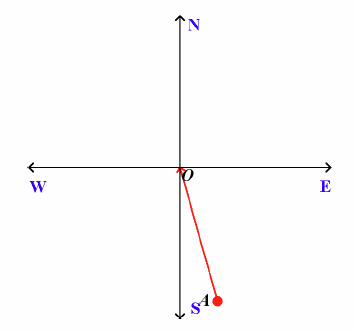
Write the true bearing of A from O if ∠SOA = 38°.
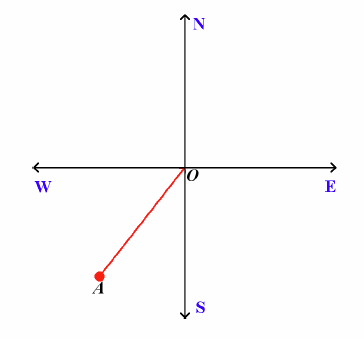
218°T
200
The angle of elevation of the top of the Perth bell tower from a distance of 85m from the tower is 44.04°.
Calculate the height of the Perth bell tower correct to the nearest tenth of a metre.
The height of the tower is 82.2 metres.
(Let BC be the height of the tower.
Now in triangle ABC
tan44.04° = (BC)/85
hence BC = 85tan44.04° ~ 82.1983)
200
In the right-angled triangle below, ∠C = 76° and AC = 9 cm. Find the length of AB, correct to two decimal places.
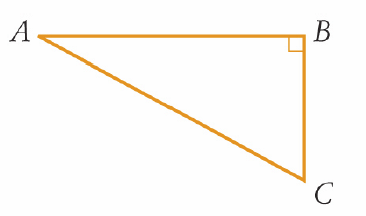
8.73 cm
(Use ‘SOH-CAH-TOA’ to help you decide whether to use the sine, cosine or tangent ratio.)
200
The graph below represents
y = –1/2 x + 3 1/2
(green) and y = –x + 3 (red). Use the graph to find the solution to the simultaneous equations.
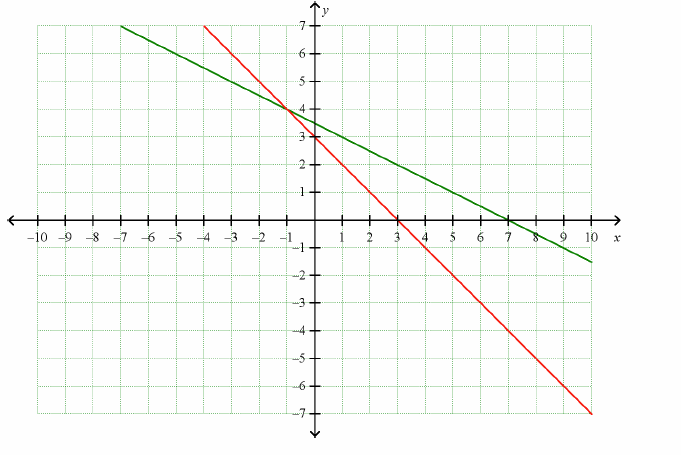
x = –1, y = 4
200
1 – 2x = –17.
x = 9
200
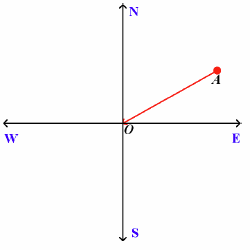
Write the compass bearing of A from O if ∠EOA = 74°.
S 16° E
300
From the top of a 80-metre cliff the angles of depression of two boats which are due West of the observer are 15° and 70°.
How far from the base of the cliff is the nearest boat? Answer to the nearest metre.
29m
300
Find the size of ∠A if a = 7 cm and c = 24 cm.Find the size of angle α if tan (α) = 1.205 (Round your answer to one decimal place, if necessary.)
16.3°
(Remember that side a is opposite ∠A, side b is opposite ∠B and side c is opposite ∠C.)
300
Solve the following simultaneous linear equations by the substitution method.
3x + g = –14
g = –3x – 14
x = –5, g = 1
300
Find the solution to
(2x+3)/3=3
x = 3
300
a) Sketch 061°T on a compass rose.
b) Sketch S 71° E on a compass rose.
400
Jack is standing on the second-floor balcony of his apartment. He measures the angle of elevation of the top of a building opposite his apartment and finds it to be 58°. Jack also measures the angle of depression of the foot of this building and finds that it is 15°.
Calculate the height of the building opposite Jack's apartment if the distance between Jack's apartment and the building is 60 metres. Give the answer to the nearest metre.
112m
400
Calculate x
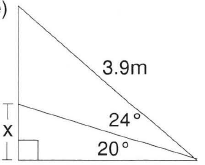
1.02 m
400
Solve the following simultaneous linear equations by the elimination method.
2e + g = 2
–e – g = –2
e = 0, g = 2
400
Find the x- and y-intercepts of 4x – 2y + 12 = 0.
x-intercept: −3, y-intercept: 6
(The x-intercept is the x-coordinate when y = 0, so solve 4x + 12 = 0.
The y-intercept is the y-coordinate when x = 0, so solve –2y + 12 = 0.)
400
A ship sails a distance of 120 km on a bearing of 44°. How far north or south will it be from its starting point? Round your answer to the nearest whole kilometre.
86 km north
(Draw a diagram.
The distance sailed will be the hypotenuse of a right-angled triangle and we can calculate the angles from the bearing given.
Trigonometry can be used to calculate the required distance.)
500
A cliff is 172 m higher than the sea. Looking out from the edge of the cliff, a boat makes an angle of depression of 24° 7 '. How far is the ship from the cliff?
384.21 m
(Draw a diagram. The angle of depression is the angle looking down from the horizontal)
500
For the given figure CD is 18.82 cm . Find the length of the perpendicular AB to the nearest millimetre.
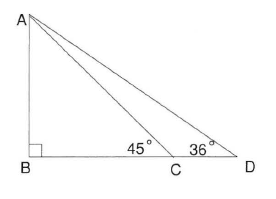
AB = 500 mm
500
Tony has a rectangular table that is 45 cm longer than it is wide. Its perimeter is 250 cm2. What is its width? Set up and solve two simultaneous equations to find the width of the table.
40 cm
(Start by letting l = length and w = width.)
500
Solve
(y^2+6)/2=3
y = 0
500
A ferry leaves port A on a bearing of S56°E and sails for 27 km to port 8. After picking up passengers the ferry sails on a bearing of N34°E for 35 km to port C.
(a) How far is port C from port A?
(b) What is the bearing of port A from port C?
Answer to nearest degree.
(a) 44.2 km (1 d.p.)
(b) S72°W