Simplifying Expressions
Exponential Scenarios
Exponential Patterns
Exponential Graphs
Solving Exponentials
100
Simplify the expression
(2x^4y^-3)^-1
y^3/(2x^4)
100
A new model of cell phone was released while the original model was still being sold. The average number of the original model sold each week was 3500, which decreased by 29% each week after the new model was released. Write an equation to determine the number of original model cell phones sold x weeks after the new model was released.
y=3500(0.71)^x
100
Sulmi did an experiment to compare two methods of warming an object. The results are shown below. Which method caused the object to warm at an exponential rate?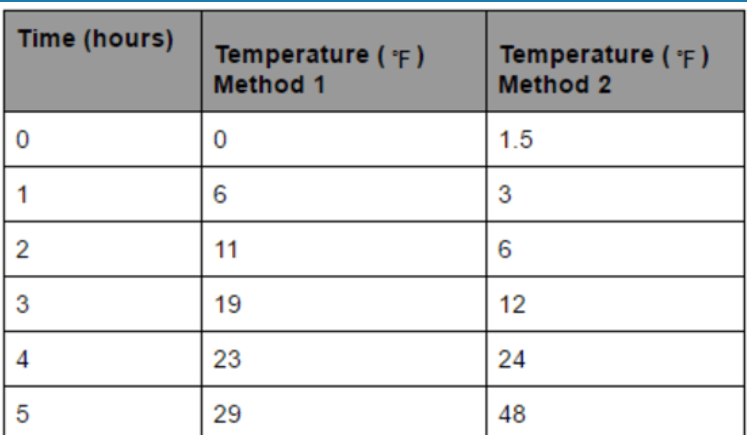 
Method 2
100
The graph below depicts a population over time. Is this a growth or decay scenario?
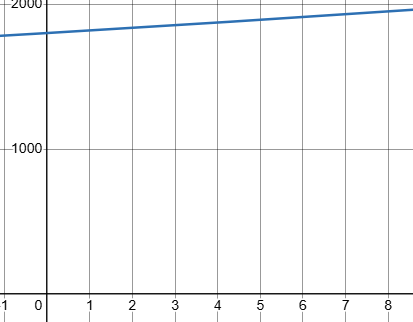
Growth
100
Solve the equation below.
3^(1-2x)=243
x=-2
200
Simplify the expression.
(3x^3y^-1z^-1)/(x^-4y^-2z^0)
(3x^7y)/(z)
200
A single bacterium is placed in a test tube and splits in two after one minute. The resulting two bacteria split in two, creating four bacteria. This process continues. How many bacteria are in the test tube after 10 minutes?
1024
200
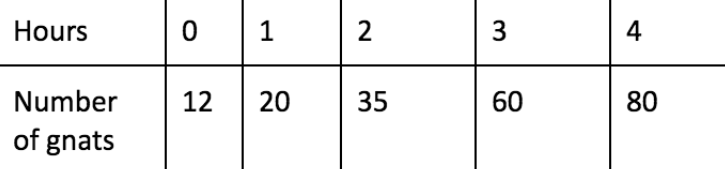What exponential function could model the number of gnats gathered by scientists after a certain number of hours, h, based on the table below?
y=12(1.7)^h
200
The graph below shows the value of a car over time. What does the y-intercept mean?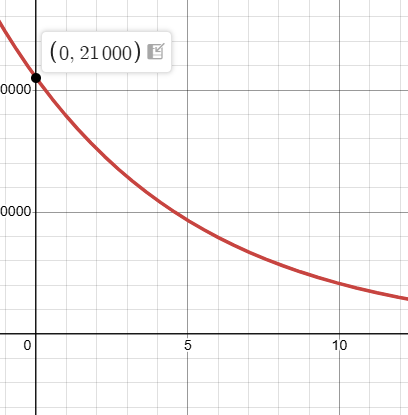 
The car's original value was $21,000.
200
When Angela was born, her grandparents deposited $5,000 into a college savings account paying 6% interest compounded continuously. How long will it take the balance in the account to reach at least $17,000?
Approximately 20.4 years
300
((3a^3b^-2)^4)/((a^-3b^7)^2)
(81a^18)/(b^22)
300
Suppose you put $960 into an account that earns 8.7% interest, compounded monthly for 3 years. How much money will be in the account after that time?
$1,245.13
300
Write an exponential function to model the data in the table below.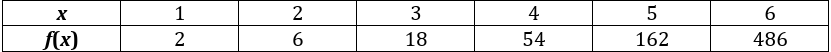 
f(x)=2/3(3)^x
300
Write an equation for the graph below assuming the rate is 1%.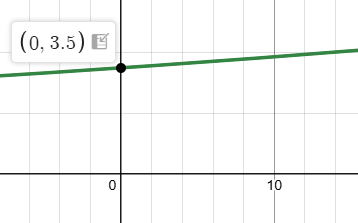 
y=3.5(1.01)^x
300
Solve the equation below.
64=16^(3x-2)
x=7/6
400
((2p m^-1q^0)^-4*2m^-1p^3)/(2pq^2)
m^3/(16p^2q^2)
400
A compound interest account that pays 2.5% interest yearly is worth $5519.06 after 4 years. How much was originally invested?
$5,000
400
Write an exponential function to model the data in the table below.
f(x)=160/3(1.5)^x
400
Write an equation for the graph below assuming the rate is 6.5%.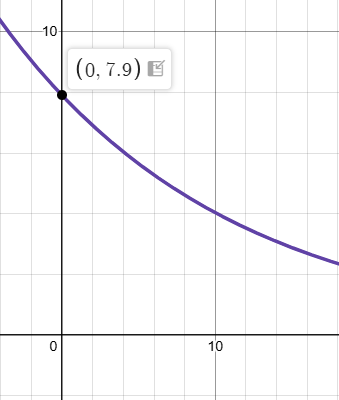 
y=7.9(0.935)^x
400
Solve the equation below.
4^(3x-2)=1
x=2/3
500
(x^(-1/2)y^4)^(1/4)/(x^(2/3)y^(3/2)*x^(-3/2)y^(1/2))
(x^(17/24))/y
500
The population of a certain species of fish triples every 5 months. Suppose there are currently 210 fish of this species. Write an equation to determine the number of fish in the population after x months.
y=210(3)^(x/5)
500
Write an exponential equation to represent the number of SMALL triangles (smallest ones you can see. This includes the purple ones and the small triangles formed in the space between the purple triangles) in any figure, x. Assume the figure on the left is the starting figure.
y=4(3)^x
500
Write an equation for the graph below.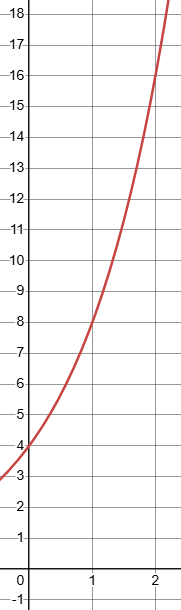 
y=4*2^x
500
When Angela was born, her grandparents deposited $5,000 into a college savings account where interest was compounded continuously. What would the interest rate in the account need to be if Angela needed the balance to be $24,000 after 18 years?
8.71%