Exponential Functions
Graphing Exponential Functions
Exponential Growth and Decay
Multiplier & Rates & Situation
100
This is what the "a" and "b" values are in
a(b)^x
What is the y-intercept (starting value) and constant multiplier (pattern)?
100
Sketch a graph of exponential growth. What is special about the multiplier when it’s growth?
What is 
100
A savings account earns 4% interest per year. If Josiah puts 500 dollars in now, this is how much will he have after 5 years
What is $608.33?
100
Given $1000 compounded an annual 12% interest rate.
How much money will be in the account in 5 years?
What is 3%?
200
This is the formula for exponential functions.
What is
a(b)^x
?
200
The graph of an exponential function will always cross the x - axis. True or false, explain your answer.
What is false.
200
The population of a small town is decreasing at a rate of 2% per year. in 1970 the population was 25,000. This is what the approximate population would be in the year 2020.
What is 9104?
200
Given the equation y=100(.93), what is the percent change?
What is 7%?
300
These ordered pairs represent an exponential function; (-1, .5),(0,3),(1,18),(2,108). True or false, explain your answer.
What is true there is a constant multiplier (6).
300
Graph
y = 2^x
300
The number of students in the book club is increasing at a rate of 15% per year and they started with 9 students. How much would they have after 7 years?
What is ~24 students?
300
Given
y = $5000(1.015)^x
What is the interest rate?
What is 1.5% annually interest rate?
400
This is the answer when f(x) = 10(5)^x is evaluated for f(3).
What is 1250?
400
Graph
y = 4(1/2)^x
400
Joanna deposited $4000 in an account in her TD Bank, earning 8.3% interest, compounded annually. She made no deposits or withdrawals. A)Write an equation that can be used to find S, her account balance after t years.
B) How much would her investment appreciate from now until 5 years?
A) What is S=4000(1+.083)^t?
B) $1959
400
Given
y = $5000(1.08)^x
What is the multiplier?
What is 1.08?
500
The graph of an exponential function, V, passes through the points (0, 2) and (3, 128) as shown on the graph below. Write an equation for the function V(x).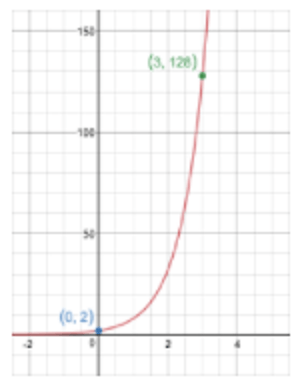
What is
V(x) = 2(4)^x
500
Find the equation that models the following table.
What is
y = 3(2)^x
500
A motorcycle was purchased for $15,000. Research shows that the motorcycle has an average yearly depreciation rate of 17.5%.
A)Create a function that will determine the value, V(t), of the motorcycle t years after purchase.
B) Determine, to the nearest cent, how much the car will depreciate from year 6 to year 7.
What is V(t) = 15000 (1-.175)^t? or 15000 (.825)^t
What is 828.14?
500
Given
f(x) = $5000(1.08756)^x
A) Find the percent change.
B) Evaluate f(7).
What is the 8.756?
What is 8997.929511?