Growth or Decay?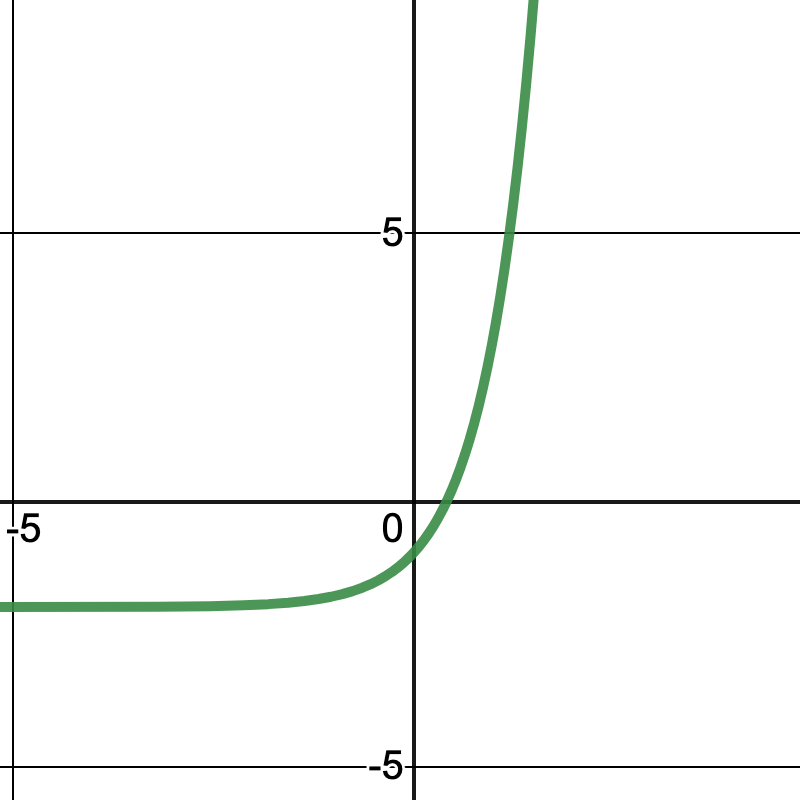
Y-intercept & Asymptote
Characteristics of Exponential Functions
Transformations of Exponential Functions
Solving Exponential Equations
100
Growth or Decay?
Growth because the graph is always increasing
100
What is the asymptote for any exponential functions BEFORE any transformations?
x-axis, i.e. y=0
100
What is the domain of the function?
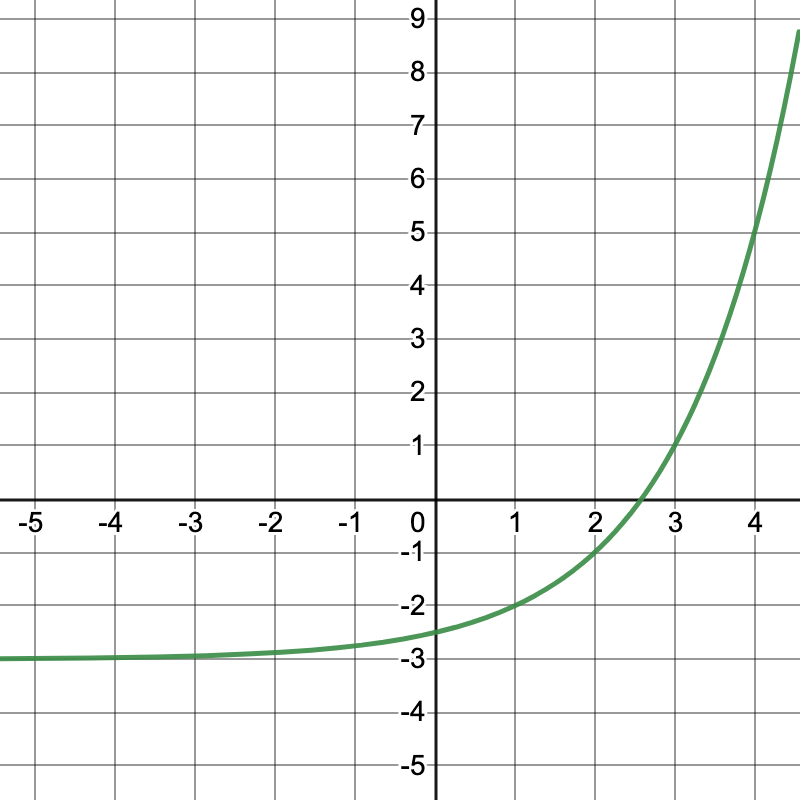
All x-values can be used, making the domain
(-oo,oo)
100
What is the vertical shift of the following function?
f(x)=-1/2(2^{x-4})
There is no vertical shift. There is no +/- sign at the end of the function.
NONE
100
Solve for x.
9^{3x-7}=9^{5-x}
x=3
Since the bases are the same, set the exponents equal to each other and solve.
9^{3x-7}=9^{5-x}
3x-7=5x-x
x=3
200
What is the parent function of the following exponential function?
1/2(4^{x+9})-10
4^x
because it has the x as the exponent
200
What is the y-intercept for ANY exponential function BEFORE major transformations?
Because of the zero exponent rule, it is (0,1)
200
What is the range of the following function?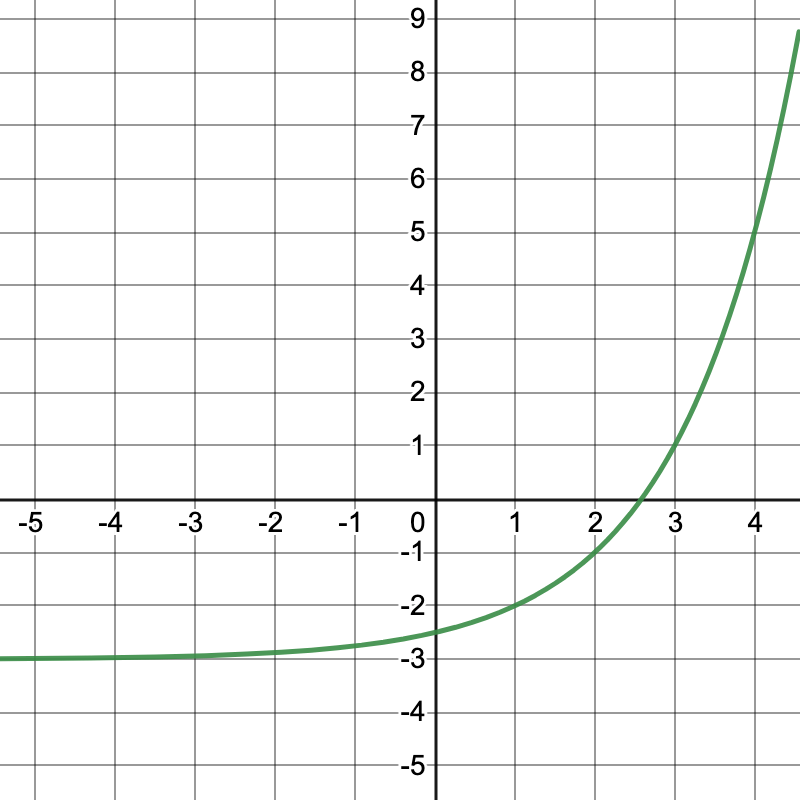
(-3,oo)
The y-values only go as low as -3.
200
What is the horizontal shift of the following function?
f(x)=-1/2(2^{x-4})
Right 4
X's LIE! It says (x-4), but negative means right.
200
Solve for x.
2^{x+4}*2^{4x+6}=2^{2x+1}
x = -3
The bases are already the same, so we just need to combine the left side by adding the exponents. (Remember your exponent rules!)
2^{x+4}*2^{4x+6}=2^{2x+1}
2^{(x+4)+4x+6}=2^{2x+1}
2^{5x+10}=2^{2x+1}
5x+10=2x+1
x=-3
300
Growth or Decay?
f(x)=5(2/3)^x
Decay because
2/3 < 1
300
What is the asymptote?
f(x)=3^{x-1}-6
y=-6
(Look at the vertical shift)
300
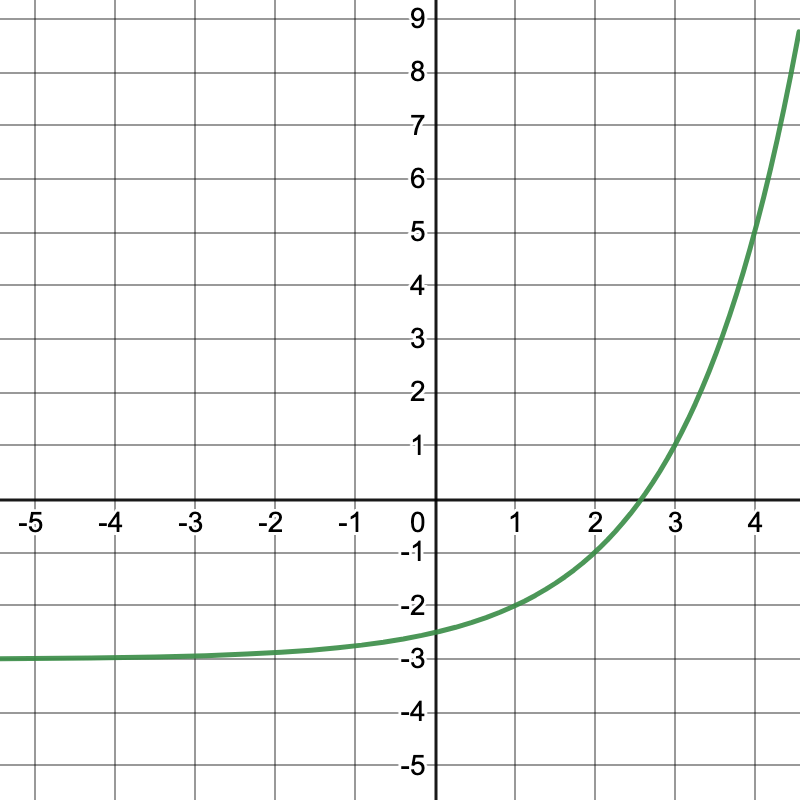
End Behavior: As x->oo, f(x)->_
oo
Looking to the right of the graph, the y-values continue forever.
300
What does the negative sign indicate?
f(x)=-1/2(2^{x-4})
Reflection across the x-axis
300
Solve for x.
49^{x+1}=343^{2x}
x=1/2
Rewrite each one so they have the same base. For this problem, the common base would be 7. Then, multiple the exponents.
49^{x+1}=343^{2x}
(7^2)^{x+1}=(7^3)^{2x}
7^{2x+2}=7^{6x}
2x+2=6x
x=1/2
400
Growth or decay?
f(x)=1/3(6/5)^x
Growth because
6/5 > 1
400
What is the y-intercept for the function below? WITHOUT DOING ANY MATH
1/2(3^x)
Since there are no big transformations, it is just the number in front, i.e.
(0,1/2).
400
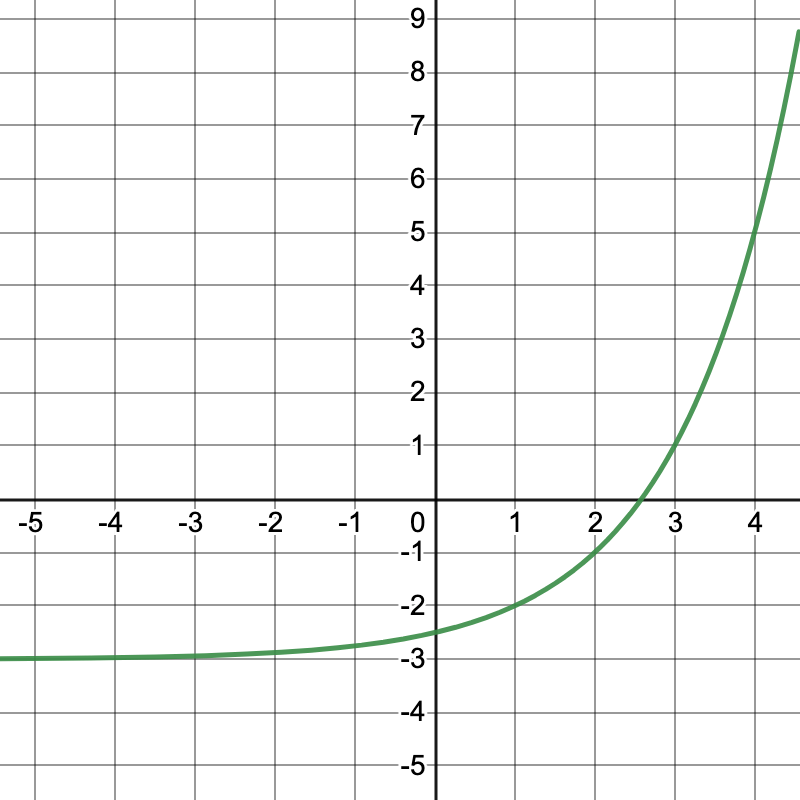
End Behavior: As x->-oo, f(x)->
-3
Looking on the left side of the graph, the y-values never passes -3. It never touches the -3, but it is still approaching -3.
400
What does the 1/2 indicate?
f(x)=-1/2(2^{x-4})
Vertical Compression since 1/2 < 1
It is getting closer and closer to the x-axis
400
Solve for x.
(1/4)^{2x}=32^{4x-2}
x=5/12
Rewrite each one so they have the same base. For this problem, the common base would be 2. Then, multiple the exponents.
(1/4)^{2x}=32^{4x-2}
(2^{-2})^{2x}=(2^5)^{4x-2}
2^{-4x}=2^{20x-10}
-4x=20x-10
x=10/24=5/12
500
Write a possible parent function for this graph.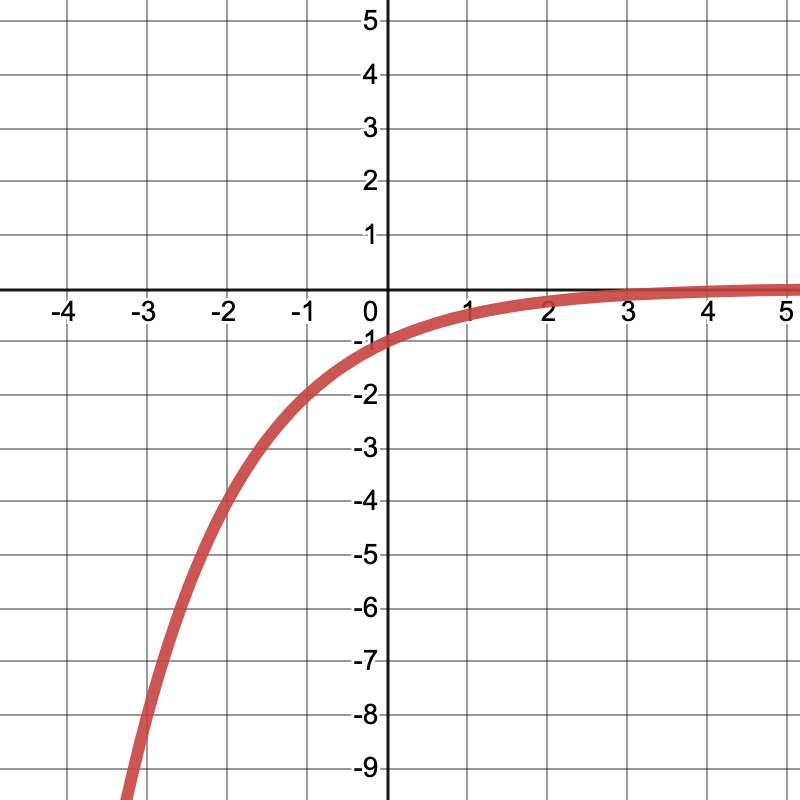
Anything with -1<b<0
Ex) 1/2, 1/3, 1/4, 2/5
It is a decay function that has been reflected, so the parent function needs to be a fraction (not an improper fraction)
500
What is the y-intercept for the following function?
-2(1/3)^{x}-3
Plug 0 in for x.
(0,-5)
500
Sketch the function:
-2(4^x)-1
Growth
Reflection over x-axis
Asymptote: y = -1
Y-intercept: (0,-3)
500
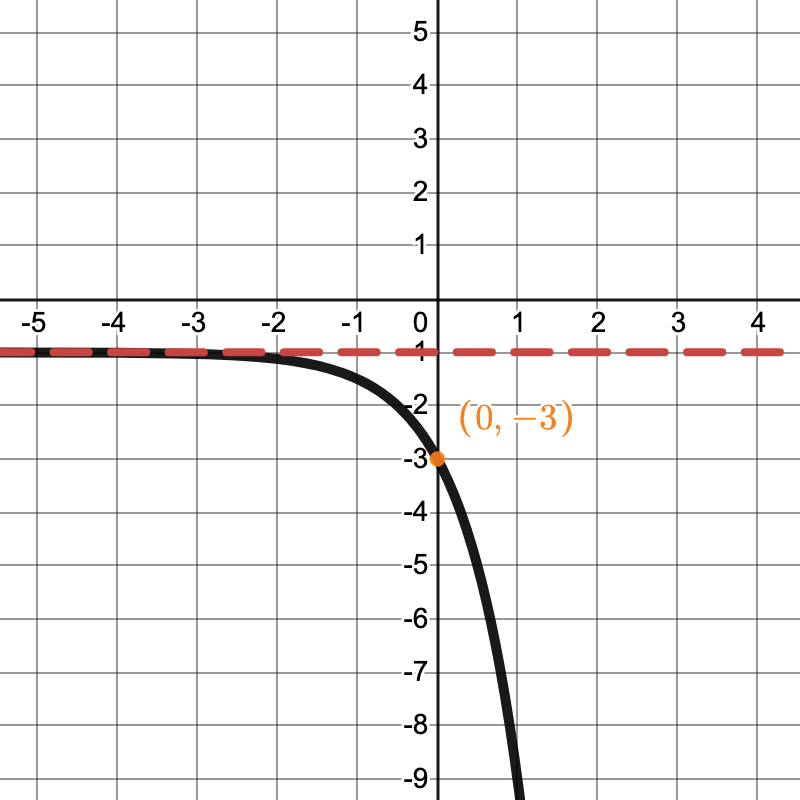
Write an equation to represent the new function:
Parent Function: 5^x
Reflection across the x-axis
Vertical stretch by a factor of 3
Horizontal shift Right 2
Vertical Shift Down 1
f(x)=-3(5^{x-2})-1
500
Solve for x.
36^{x-3}*216^x=216^{2x+1}
x = -9
Rewrite each with the same based, add necessary exponents, and set equal to each other.
36^{x-3}*216^x=216^{2x+1}
(6^2)^{x-3}*(6^3)^x=(6^3)^{2x+1}
6^{2x-6}*6^{3x}=6^{6x+3}
6^{5x-6}=6^{6x+3}
5x-6=6x+3
x=-9