Properties of Exponents
Exponential Functions
Graphing Exponential Functions
Negative and Zero Exponents
Initial Amount, Growth Factor, and Growth Rate
100
Simplify
c^18/c^6
What is
c^12
?
100
This is what the "a" and "b" values are in
a(b)^x
What is the y-intercept (starting value) and constant multiplier (pattern)?
100
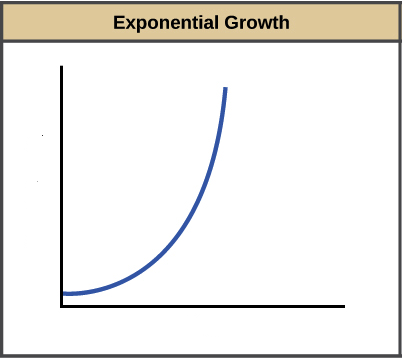
Sketch a graph of exponential growth. What is special about the multiplier when it’s growth?
What is 
100
Simplify: 6tv^0
6t
100
Use y = 250(1.2)^t What is the initial?
What is 250?
200
Simplify
(28n^9)^0
What is
1
?
200
This is the formula for exponential functions.
What is
a(b)^x
?
200
The graph of an exponential function will always cross the x - axis. True or false, explain your answer.
What is false.
200
Simplify: (4^2)(x^(-2))
8 / x^2
200
Use y = 250(1.2)^t What is the growth factor?
What is 1.2?
300
Simplify
-5x^-3
What is
-5/x^3
300
These ordered pairs represent an exponential function; (-1, .5),(0,3),(1,18),(2,108). True or false, explain your answer.
What is true there is a constant multiplier (6).
300
Graph
y = 2^x
300
Simplify: 4(x^-2)(g^3)
4g^3 / x^2
300
Use y = 25(0.4)^t What is the growth factor?
What is 0.4?
400
Simplify
(-3us^8d^2)^4
What is
81u^4s^32d^8
400
This is the answer when f(x) = 10(5)^x is evaluated for f(3).
What is 1250?
400
Graph
y = 4(1/2)^x
400
Simplify: ( (4^-2)(x^-5)(y^-9)(z^-3) )^0
1
400
y = 9.8(1.35)^t What is the growth factor?
What is 1.35?
500
Simplify
(20q^5p^-1)/(5q^3p^8)
What is
(4q^2)/p^9
500
The graph of an exponential function, V, passes through the points (0, 2) and (3, 128) as shown on the graph below. Write an equation for the function V(x).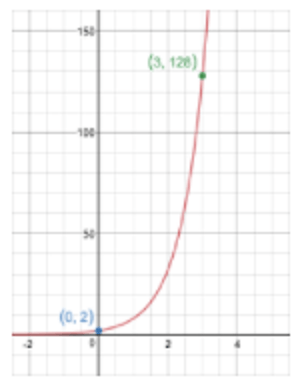
What is
V(x) = 2(4)^x
500
Find the equation that models the following table.
What is
y = 3(2)^x
500
( (x^-2)(y^2) ) / ( (b^-4)(c^4) )
( (b^4)(y^2) ) / ( (c^4)(x^2) )
500
y = 9.8(1.35)^t What is the initial rate?
What is 9.8?