Characteristics
Applying Exponential Equations
Average Rate of Change
Writing Exponential Functions
Random
100
Describe all of the characteristics of the function: f(x) = 2^x
growth
100
The population in the town of Huntersville is presently 38,300. The town grows at an annual rate of 1.2%. Find the number population of the town after 9 years.
Approximately 42,640 people
100
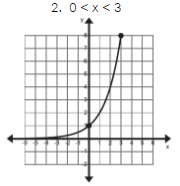
Calculate the average rate the change on the interval [0,3].
7/3
100
Write an exponential growth function to model the situation.
A population of 422,000 increases by 12% each year.
What is f(x) = 422,000(1.12)^x
100
Describe the transformations of the f(x)
f(x)= -4(3)x - 5
Reflection, Vertical Stretch, Shift Down
200
Describe all of the characteristics of the function: f(x)=100(0.5)^x
decay and vertical stretch
200
$1,200 is invested at an annual rate of 3.2%. How much money will the account have after 12 years?
$1751.21
200
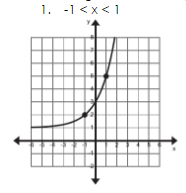
Find the average rate of change over the given interval [-1, 1].
What is 1.5
200
The population of Baconburg starts off at 20,000, and grows by 13% each year. Write an exponential growth model and find the population after 10 years.
What is f(10) = 20,000(1.13)^10 and population of 67,891
200
The model P(t)=100(4)t represents the population P(t) of a bacteria over t years. How long does it take for the population of the bacteria to double?
6 months
300
Describe all of the characteristics of the function: f(x)=-6(1.4)x+2
Decay, Reflection, Vertical Stretch, Shift Up
300
The population in the town of Deersburgh is presently 42,500. The town has been growing at a steady rate of 2.7%. What will the population of the town be in 5 years?
Approximately 42, 499 People
300
Calculate the average rate of change of the function
f(x)=2/3(4)^x-2
2560
300
The Hippityhoppity bunny decided to have a family reunion at the Magic Forest every 5 years. During the second reunion the family discovered that the number of family members was 154 and was growing at an annual rate of 3.2%.
Write an equation to model the growth of the bunny family.
What is f(x) = 154(1.032)^x
300
What is the average rate of change of y = 2(3)x at [2, 4]?
72
400
Describe all of the characteristics of the function: f(x)=-1/4(3/8)^x+12
Growth, Reflection, Vertical Compression, shift up
400
The value of a car was $22,000 when it was purchased. They car depreciates at a rate of 19% per year. How much will the car be worth in 8 years?
$4,076.64
400
Calculate the average rate for the function
p(t)= 9.8(1.35)t on the interval [0,1].
3.43
400
The fish in The Magic Forest Lake were declining at an annual rate at 1.5%. Their current number is estimated at 2500.
Write an equation to model the decreasing number of fish.
What is y = 2500(.985)^x
400
Jimmy purchased a rare coin for $350. It will appreciate (increase) in value by about 6% each year. Write the equation that represents this.
f(x)=350(1.06)x
500
Sasha was given the parent function f(x)=3x. If she wants to create a function that is a decay function, compressed and shifted up what should she do?
-a, 0<|a|<1, and +k
500
The value of a stock when purchased is $10 a share. However, over the past 5 days the price went down at a constant rate of 4%. How much is the stock worth now?
$8.15
500
Given the function f(x)=-3(2)x determine if the slope is negative and positive.
negative
500
The squid in The Magic Forest Lake were declining at an annual rate at 5.5%. Their current number is estimated at 50,000.
Write an equation to predict the number of squid in the lake in 10 years.
What is f(10) = 50000(.945)^10 and 28,398 squid
500
Suppose you deposit $15,000 into an account earning 8% interest compounded quarterly. To the nearest dollar, what is the balance after 8 years?
$28268.11