Exponential Growth & Decay
Annual Interest
Evaluating Logs
Log Properties
Solving Equations
100
Find the y-intercept and write as an (x,y)-coordinate:
y=1.19*(4)^x
(0,1.19)
100
Convert the percent value to a decimal: 7.4%
0.074
100
Evaluate the logarithm:
log1000
log1000=3
100
Rewrite as a single logarithm:
log_2 7 + log_2 9
log_2 63
100
Solve the following equation:
2^(2x)=16
x=2
200
Find the y-intercept and write as an (x,y)-coordinate:
y=(0.33)^x
(0,1)
200
Convert the decimal value to a percent: 0.0031
0.31%
200
Evaluate the logarithm:
log_6 216
log_6 216=3
200
Rewrite as a single logarithm:
2log y - log 6
log frac{y^2}{6}
200
Solve the following equation:
9^(n+1)=3
n=-frac{1}{2}
300
What is the term for a line that an exponential growth or decay function will approach but never touch?
Asymptote
300
What is the annual rate of interest, written as a percentage, of the savings account modeled by this equation?
A(t)=45.1(1.072)^t
7.2%
300
Evaluate the logarithm:
log_7 frac{1}{49}
log_7 frac{1}{49}=-2
300
Evaluate the logarithm (rounded to the nearest hundredth):
log_5 17
log_5 17=1.76
300
Solve the following equation (with answer rounded to the nearest hundredth):
7^x=25
x=1.65
400
What is the equation of the form
y=ab^x
that matches this graph?
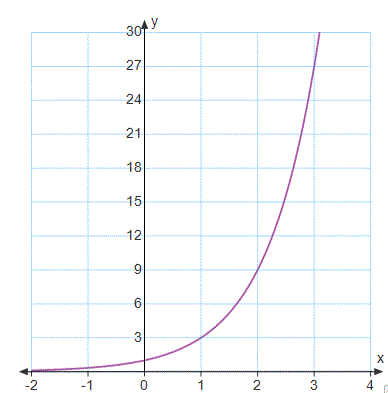
y=3^x
400
What is the equation of the form
A(t)=a(1+r)^t
that matches this situation?
You put $3000 into a college savings account. The account pays 5% interest annually.
A(t)=3000(1+0.05)^t
or
A(t)=3000(1.05)^t
400
Evaluate the logarithm:
log_16 64
log_16 64=frac{3}{2}
400
Expand the logarithm fully:
log_4 (3x)^5
5log_4 3 + 5log_4 x
or
log_4 243 + 5log_4 x
400
Solve the following equation (with answer rounded to the nearest hundredth):
3^(y-5)=8
y=6.89
500
What is the equation of the form
y=ab^x
that matches this graph?
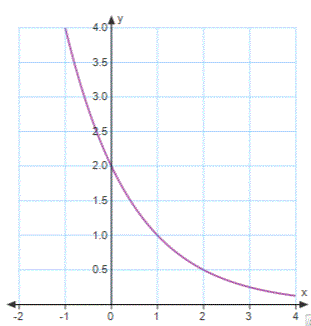
y=2(1/2)^x
500
If you put $2500 into a savings account that pays 6.4% interest annually, how much money will be in the account after 4 years (rounded to the nearest cent)?
$3204.10
500
Evaluate the logarithm:
log_625 frac{1}{125}
log_625 frac{1}{125}=-frac{3}{4}
500
Expand the logarithm fully:
log_3 sqrt(frac{m}{n})
frac{1}{2}log_3 m - frac{1}{2}log_3 n
500
Solve the following equation:
log_7 (16x+23)=3
x=20