Change a log
Compound Interest
Continuous Interest
Exponents
Solve it!
(log solutions as log or ln only)
(log solutions as log or ln only)
Properties of Logarithms!
100
log_(1/2)(256)=-8
(1/2)^(-8)=256
100
You receive $5000 to invest in a bank account paying 4.5% interest compounded annually. If you leave the money in there for 15 years, how much will you have?
$9676.41
100
How much will you have at the end of 5 years if you leave $610 in an account with 8.4% interest compounded continuously?
$928.40
100
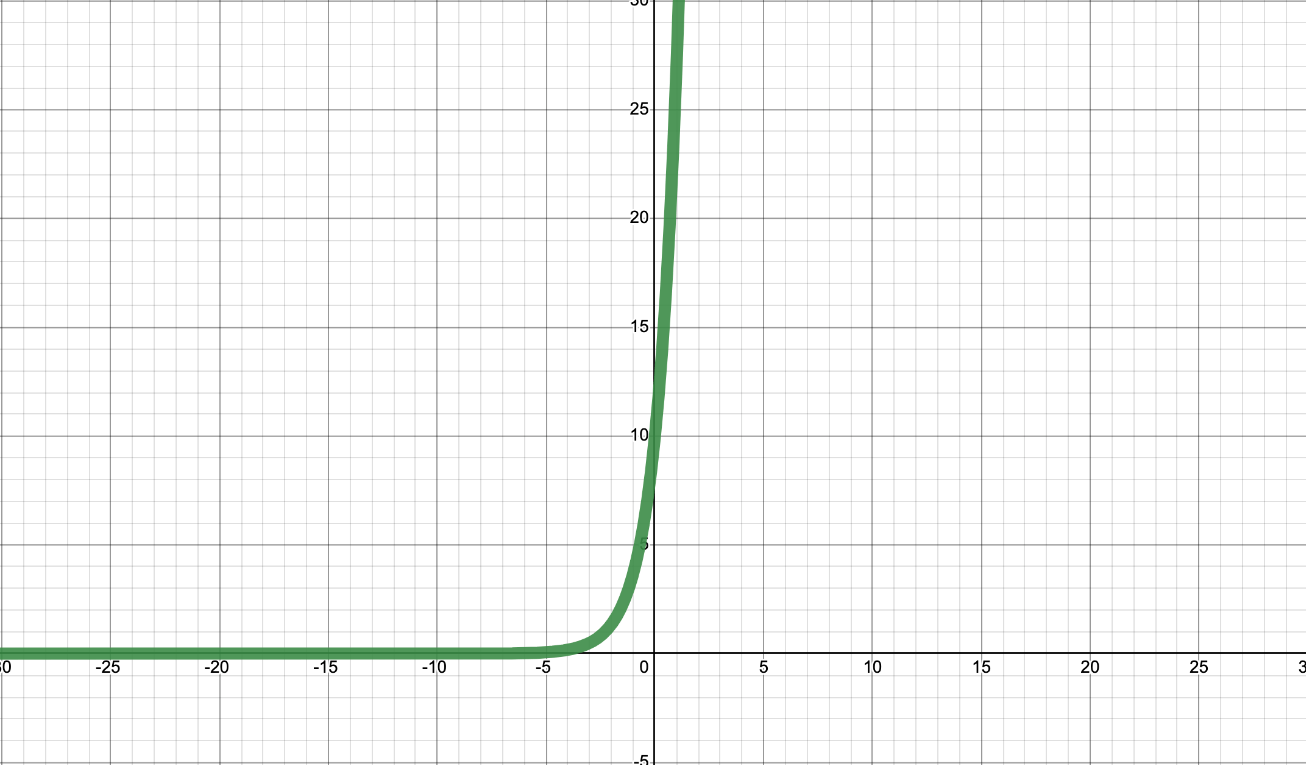
What is the domain of
y=10e^x
The domain is all real numbers!
100
Solve 2x = 3
x=log(3)/log(2)
or
x=ln(3)/ln(2)
100
Condense the following logarithm:
log(4)+log(x)-log(z)
log((4x)/z)
200
log(5)=b
10^b=5
200
You receive $200 to invest in a bank account paying 12.1% interest compounded monthly. If you leave the money in there for 5 years, how much will you have?
$365.14
200
How much should you invest at 4.8% compounded continuously to have $5000 in 2 years.
$4542.32
200
Define an exponential equation p(t) for the following:
A colony of bacteria begins with 52 organisms and the population quintuples each day!
How many bacteria are present after 3.4 days?
p(t)=52(5)^t
12373.7506 bacterial organisms based on our model
200
Solve 2x-1 = 17
x=(ln(17)+ln(2))/ln(2)
or
x=(log(17)+log(2))/log(2)
200
Expand the following logarithm:
log_9((2x^2)/y^8)
log_9(2)+2log_9(x)-8log_9(y)
300
log_w(m)=a
w^a=m
300
What amount must you invest in a bank account paying 11.1% interest compounded annually if you wish to have $10000 after 8 years?
$4308.12
300
How much should you invest at 9% compounded continuously to have $10000 in 8 years.
$4867.52
300
Change forms!
x^2-2x-3=(2x-2)^(e^(x-1))
log_(2x-2)(x^2-2x-3)=e^(x-1)
300
Solve
log(x^2+1)-log(2)=log(13)
x=5,-5
300
Condense the following logarithm:
2ln(y)+ln(x^3)/2-ln(z)
ln((y^2x^(3/2))/z^2)
400
log_(x-1)(15)=(x+1)
(x-1)^(x+1)=15
400
If you invest $50 in a bank account paying 12% interest compounded quarterly, how long does it take if you wish to have $200?
t = 11.72 years
400
How long should you invest $10001 at 4.8% compounded continuously to have $5000?
(No Typo!!!!)
t = -14.4426 years or (go backward in time 14 years 161 days 13 hours 36 minutes and 34.343 seconds!)
400
What is the range of
y=-2(1/3)^(x-1)-3
(-infty,-3)
400
Solve
log_2(x-1)+log_2(x)=1
x=2
400
Expand the following logarithm:
log_166((11*10^3)/(7z^5))
log_166(11)+3log_166(10)-log_166(7)-5log_166(z)
or
log_166(11)+3log_166(10)-(log_166(7)+5log_166(z))
500
ln(x^2-15x+56)=-17
e^(-17)=x^2-15x+56
500
If you invest $322 in a bank account paying 2.2% interest compounded daily, how long does it take if you wish to have $400?
t= 9.86 years
500
What is the rate of the account giving you $13000 at the end of 6 years when you initially invested
$e^8
r=.2455 or r=24.55%
500
For the exponential equation that goes through points (9, 140) and (10, 250) find the a and b values exactly and their approximations!
y=a(b)^x
a=250/(25/14)^10 approx .7583
or
b=25/14 approx 1.7857
500
Solve
2^x=5^(x-1)
x=ln(5)/(ln(5)-ln(2))
x=log(5)/(log(5)-log(2))
500
Condense the following logarithm:
log_2(x)+log_5(y)-2log_2(z)+log_5(k)
log_2(x/(z^2))+log_5(yk)