Interest of all sorts!
Exponents!
Logarithms!
Solve it!
Potpourri
100
r = 4.8%
P = $5000
t = 2 years
n = 55
5503.56
100
Describe the domain, range, asymptote, and end behavior.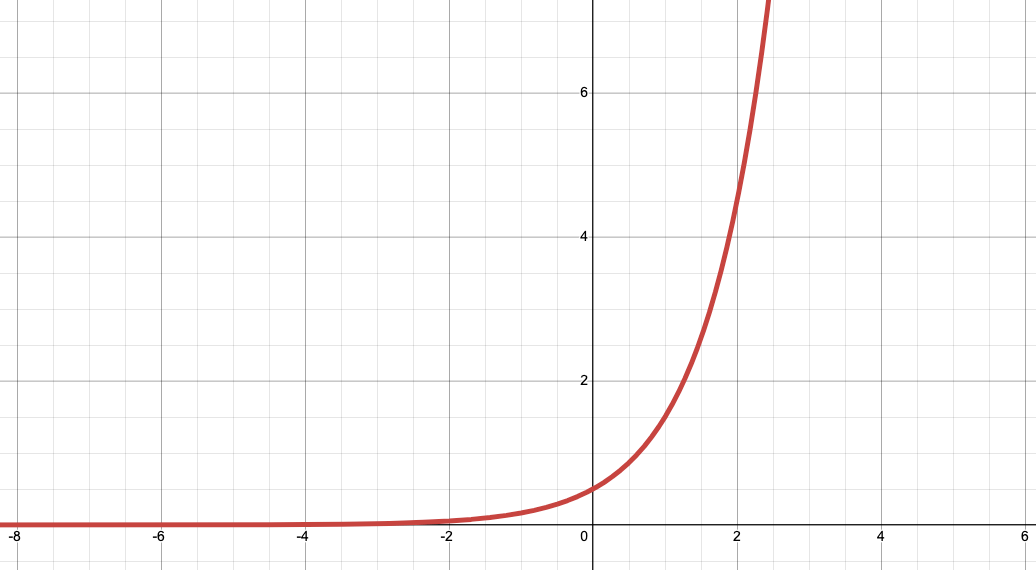
domain is all real numbers
range is
(0, infty)
asymptote is y=0
end behavior:
x->-infty, y->0
x->infty, y->infty
100
Evaluate the logarithm
log_3(27)
3
100
Solve 22x = 4-x+1
x=1/2
100
Name this item!
A Natural Log!
200
r= 11.1%
n=continuously
A= $10000
t= 8 years?
$4114.78
200
Joe buys a car for $33000 brand new. His car depreciates in value by 8.4% each year. What will Joe be able to sell his car for 8 years later?
Joe's car is worth $16356.02 in 8 years
200
Expand the following logarithm:
log_7((10x^3)/y^(-8))
log_7(10)+3log_7(x)+8log_7(y)
200
log_3(3x^2+5) = log_3(8x)
x=5/3 or x=1
200
What is the minimal number of x-intercepts for an odd degree polynomial?
One!
300
r= 9% A= $10000 in t= 8 years
compounded continuously
$4867.52
300
log_2(4)-log(1000)
-1
300
Evaluate the logarithmic expression
log_(b^2)(b)+log_(a^5)(a^5)
3/2
300
Solve
log(x^2+1)+log(2)=log(74)
x=6,-6
300
What type of asymptote can SOMETIMES get crossed.
Horizontal Asymptote
400
A= $13000 r=25%
P= 2980.96
t = 5.8908 years
400
What is the exponential function modeling the following data:
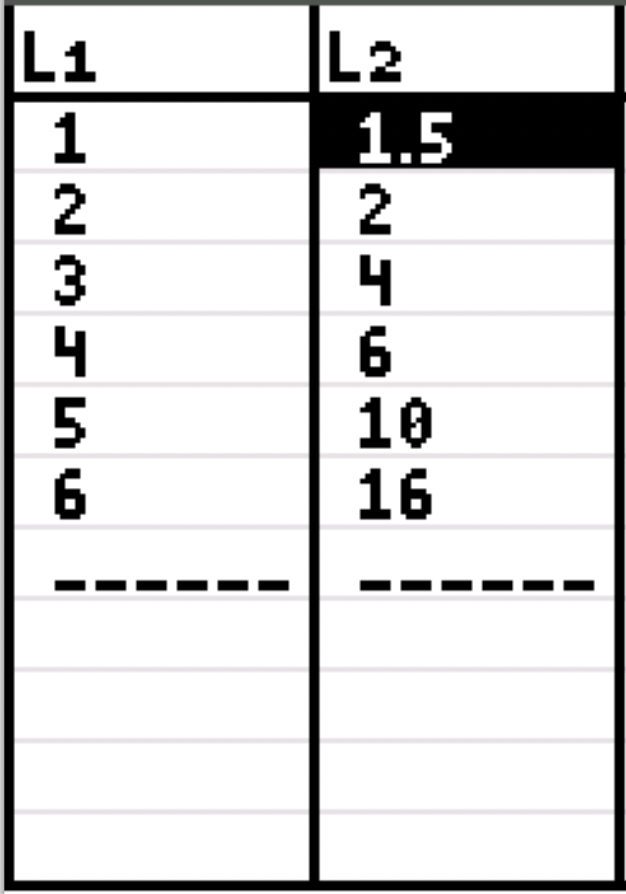
y=.8622(1.6286)^x
400
Condense the following logarithm:
log_16(11)+3log_16(10)-log_16(7)-5log_16(z)
log_16((11*10^3)/(7z^5))
400
log_(1/3)(81)-log_(81)(1/3)
-15/4
400
evaluate: i2023
i^2023=i^3*i^2020=i^3*1=i^3=-i
500
p= $322 r= ? n=12 A= $400 t= 9 years
r= 2.4126%
500
For the exponential equation that goes through points (2, 175) and (3, 250) find the a and b values exactly!
y=a(b)^x
a=343/4
b=10/7
500
Evaluate the logarithmic expression!
log_2(3)*log_3(4)*log_4(6)*log_6(8)*log_8(16)
log(3)/log(2)*log(4)/log(3)*log(6)/log(4)*log(8)/log(6)*log(16)/log(8)=log(16)/log(2)=4
500
Solve
log_6(2x-1)=2-log_6(x)
x=9/2
500
What are the x-intercept(s) for the following function:
y=root(3)(x+7)+1
(-8,0)