Writing Equations
Solving Equations
Writing Expressions
Equivalent Expressions
100
Write an equation that represents the hanger below.
4x = 8
100
Draw a tape diagram to show:
x + 10 = 12
Then, find the solution.
x = 2
100
Ms. Poland buys a diet coke for $2 and a bag of chips, b, at CVS.
Write an algebraic expression to represent the the total cost.
b + 2
100
Give an example of two equivalent algebraic expressions!
2x + 4
x + x + 1 + 1 + 1 + 1
200
Write an equation that represents the tape diagram.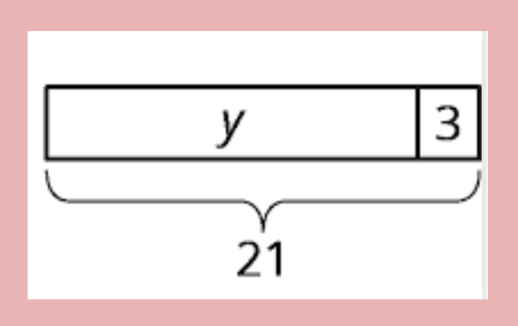 
y + 3 = 21
200
Use any strategy to solve. Then, check your work.
x = 12
200
Each gatorade costs $1.25.
Write an algebraic expression to find the cost for any number of gatorades, g.
1.25g
200
Are the two expression equivalent or not equivalent? Explain or show how you know.
3x + 9
3 (x + 3)
Yes the two expressions are equivalent. I know this because 3 groups of x + 3 is like x + 3 + x + 3 + x + 3 = 3x + 9.
300
Write an equation that represents the tape diagram.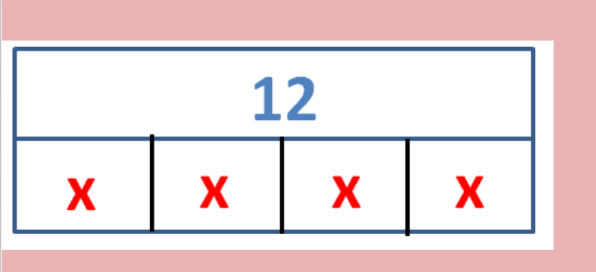 
4x = 12
300
Use inverse operations to solve. Then check, your work.
x = 4.4
300
Write an algebraic expression to find the cost of any number of pizza slices, p.
1.25p
300
Write 2 equivalent algebraic expressions to represent the picture below.
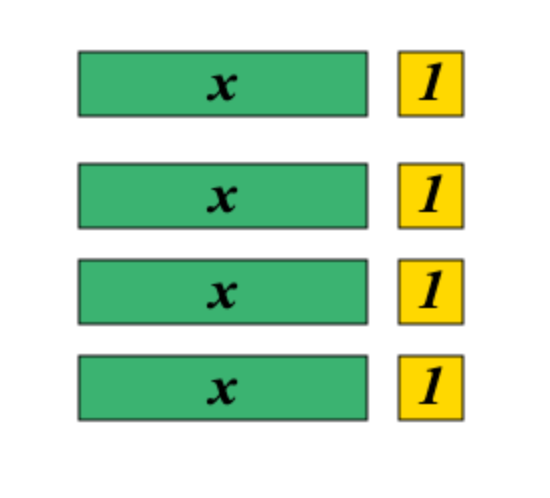
4x + 4
4 (x + 1)
400
Gabe has $35 to spend on rides at an amusement park. Each ride pass costs $5.
He can go on x rides.
Part A: Write an algebraic equation to represent the story.
Part B: Find a solution and explain what the solution means.
5x = 35
He can go on 7 rides.
400
Show your work with inverse operations. Then, check your work.
x = 5 1/4
400
Mrs. Murphy pays her daughter’s babysitter $25 per hour. She also give the babysitter a $15 tip at the end of the night.
Part A: Write an algebraic expression to find the cost of the babysitter for any number of hours, h.
Part B: How much money will the babysitter make in 3 hours?
25h + 15
She will make $90.
400
Write 3 equivalent algebraic expressions to represent the picture.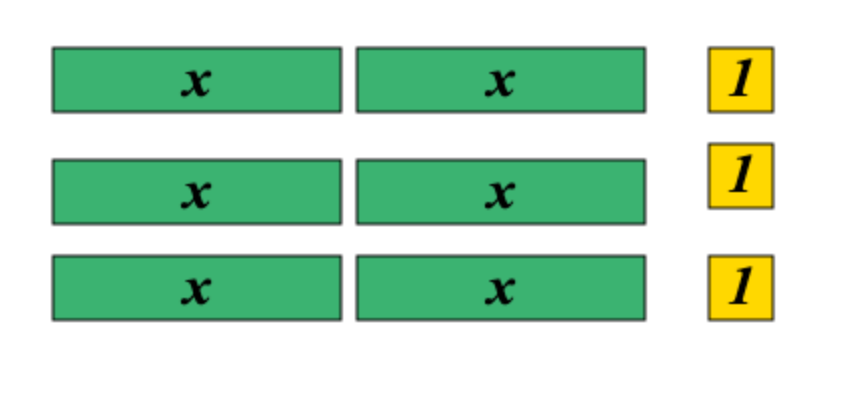 
3 (x + 1)
3x + 3
x + x + x + 3
500
Part A: Write an equation to find the number of slices, s, she needs to sell.
Part A: Solve the equation to find the number of slices needed she needs to sell to earn $100.
1.25s=100
She needs to sell 80 slices of pizza.
500
D and E
500
What is the difference between a coefficient and a constant?
Give a real-life example of each.
A coeffficient happens repeatedly.
A constant happens one time.
A coefficient is paying a gym $75 per month. A joining fee of $100 is a constant.
500
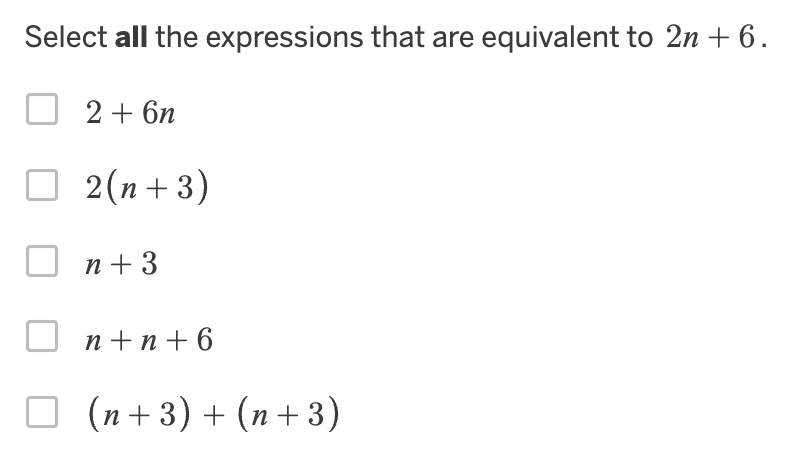
Everything but n + 3!