Binomials
Trinomials
Graphing quadratics
Vocabulary and concepts
100
(n+2)(n+3)
n2 +3n + 2n +6
n2 +5n +6
100
b2 + 8b + 7
(b+7) (b+1)
100
What are the x-intercepts of this parabola?
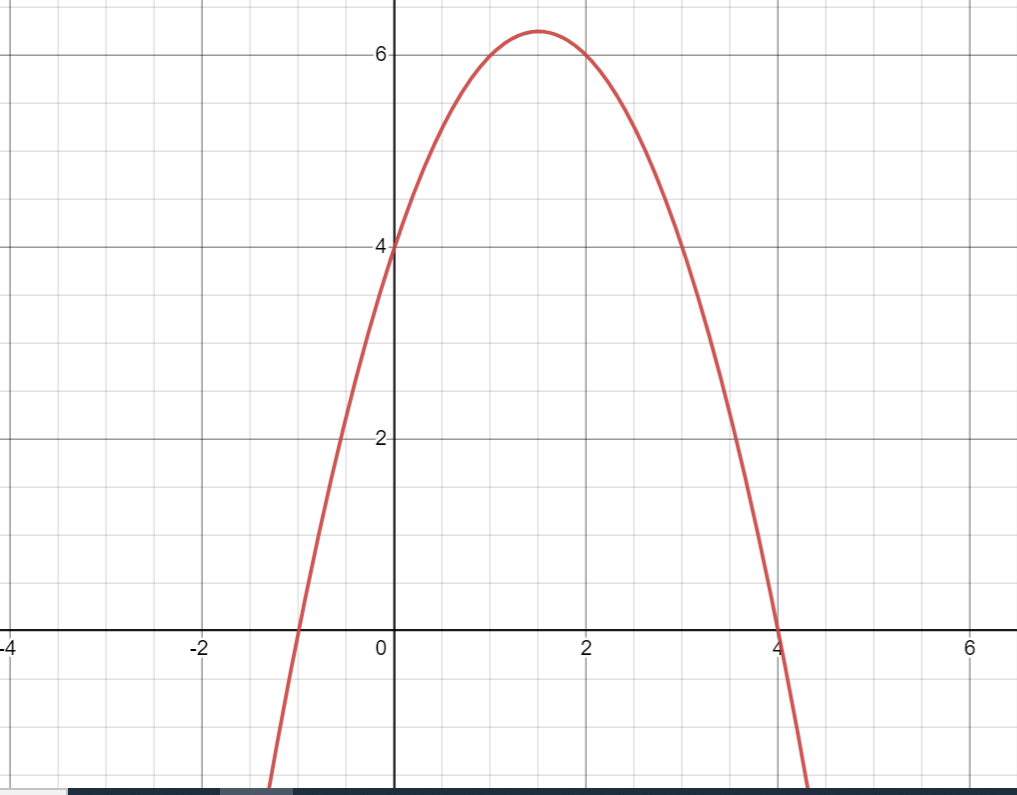
(-1,0) and (4,0)
100
What is the name of the shape a quadratic function takes when graphed?
Parabola
200
(n+1)(n+2)
n2 +2n + 1n +2
n2 +3n +2
200
b 2 + 16b + 64
(b+8) (b+8)
200
What is the equation for the line of symmetry of this parabola?
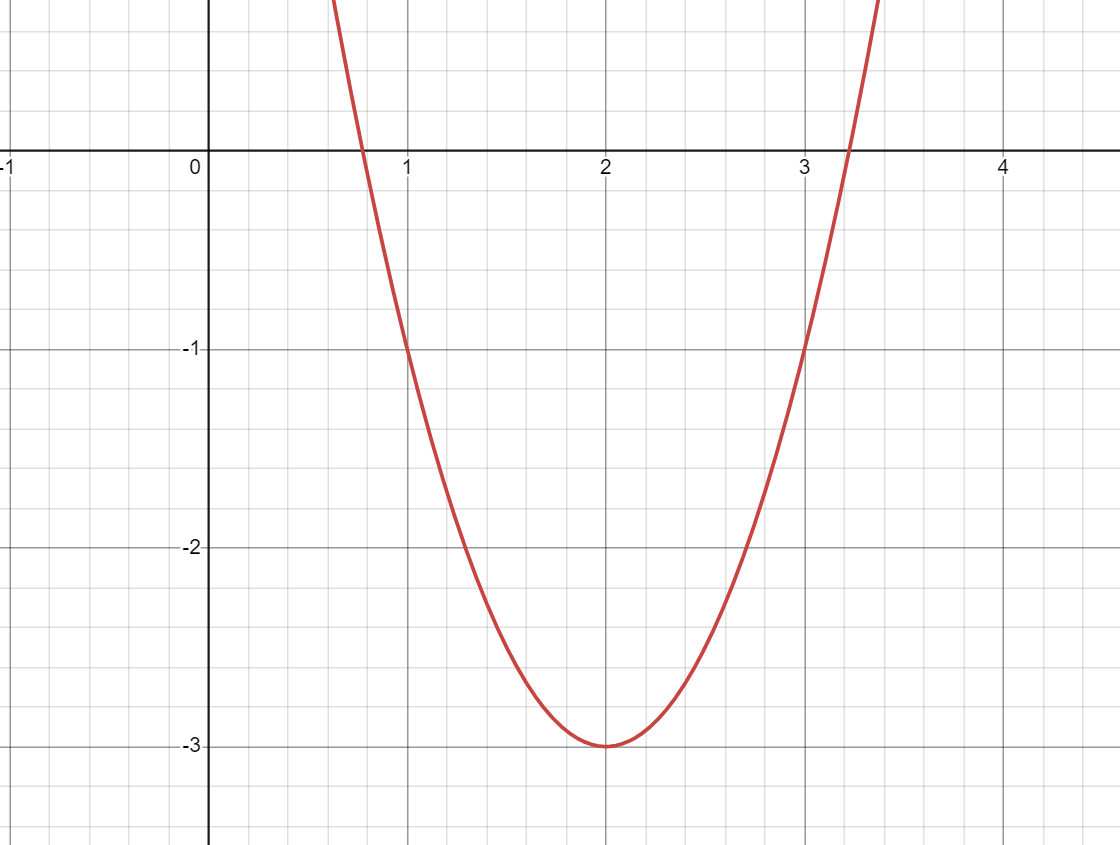
x=2
200
What is the vertex?
The highest or lowest point of the parabola. The point where the parabola changes growth directions.
300
(x+4)(x+3)
x2 +3x + 4x +12
x2 +7x +12
300
m 2 + 10m + 21
(m+7) (m+3)
300
Does this parabola have a minimum or a maximum value? What are the x-intercepts?
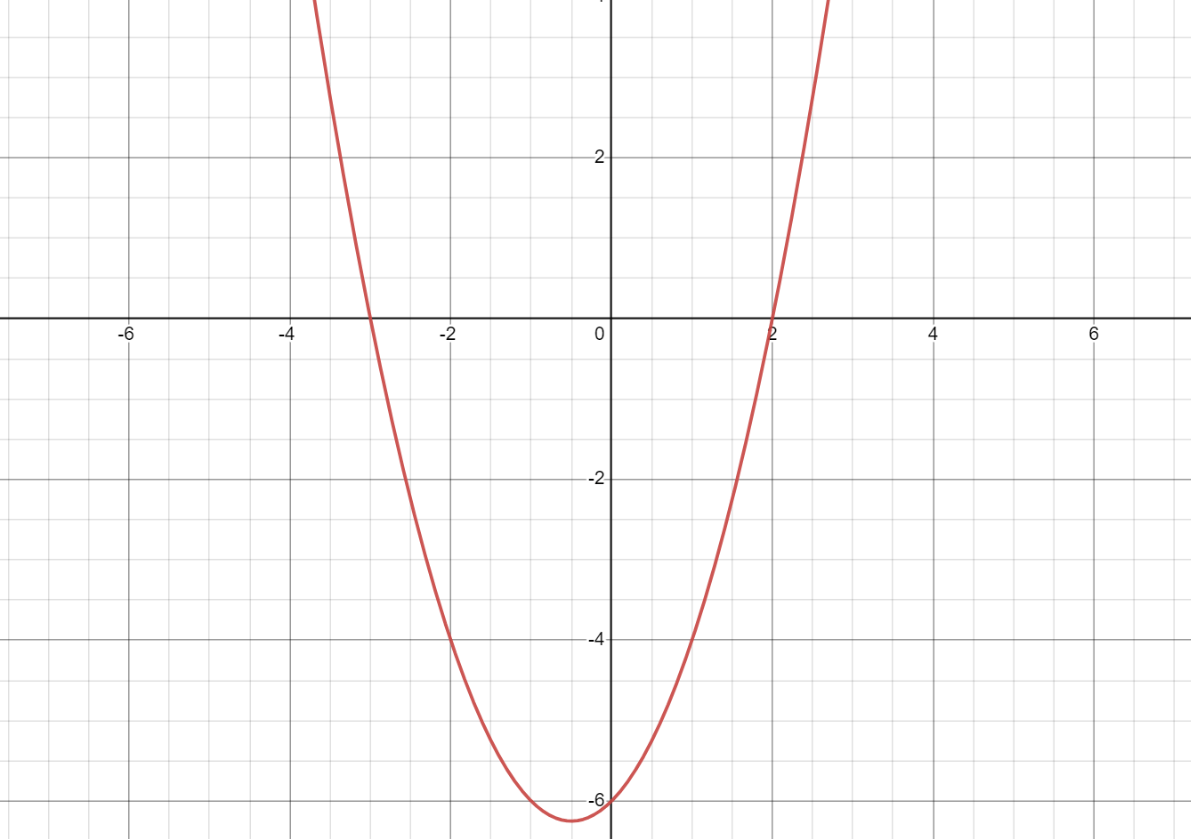
minimum
(-3,0) and (2,0)
300
What are the domain and range of a function?
Domain: The span of the function in the x-axis.
Range: The span of the function in the y-axis.
400
(r+2)(3r+9)
3r2 +9r + 6r +18
3r2 +15r +18
400
k 2 + 7k + 12
(k+4) (k+3)
400
What is the domain and range of this parabola?
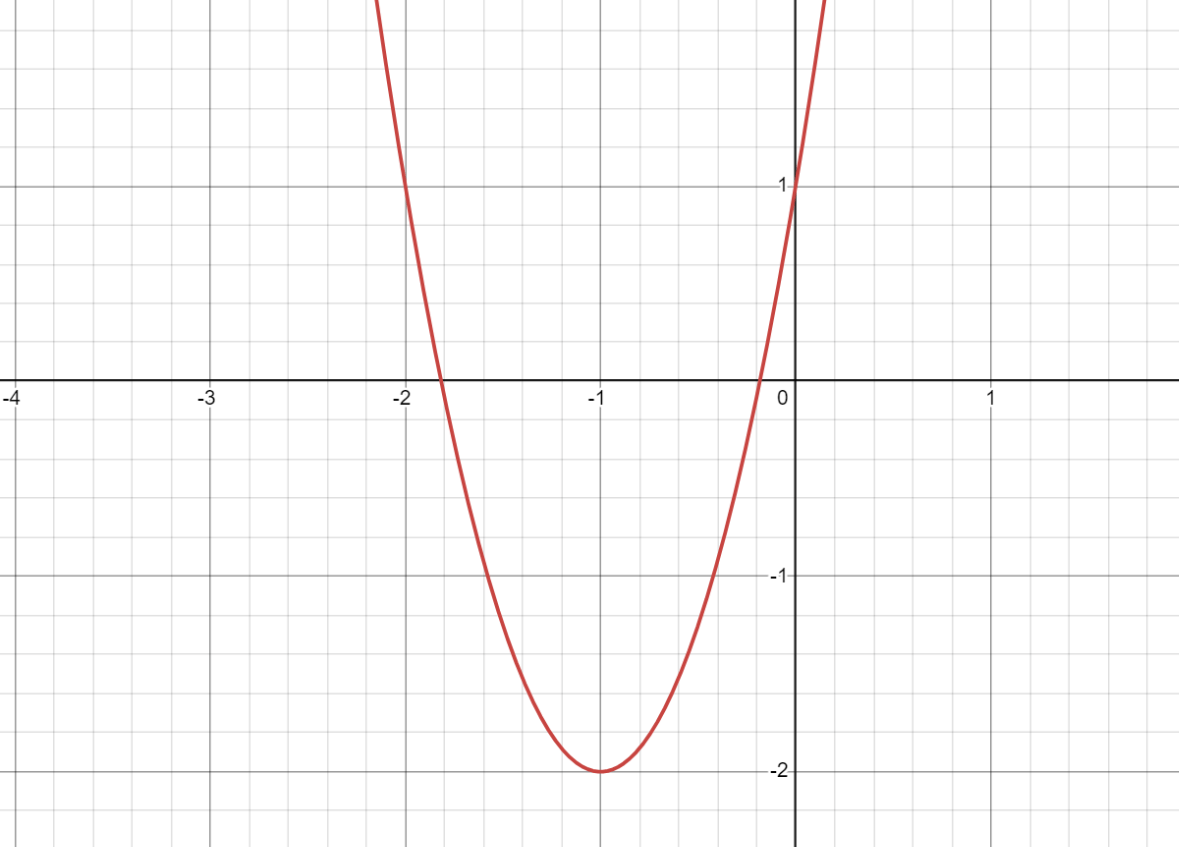
Domain: (-∞, ∞)
Range (-2, ∞)
400
What is the name of this form of expressing a quadratic function?
f(x) = Ax^2+Bx + C
Standard form.
500
(2n+10)(n+3)
2n2 +6n + 10n +30
2n2 +16n +30
500
a 2 + 11a + 18
(a+9) (a+2)
500
Identify the vertex, equation for the line of symmetry and x-intercepts in this parabola.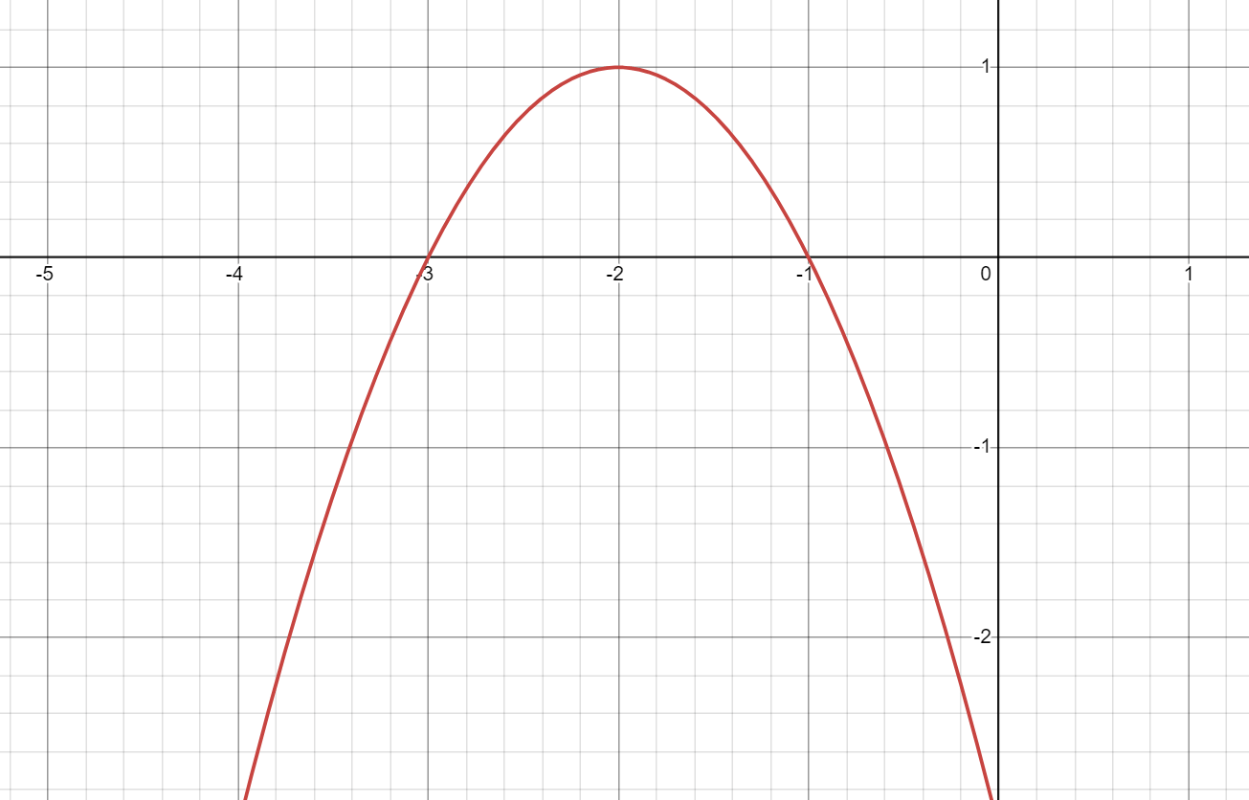 
Vertex (-2,1)
lines of symmetry equation: x=-2
x-intercepts: (-3,0) and (-1,0)
500
What do the "h" and "k" values of this equation indicate?
f(x) = a(x-h)^2+k
h = Horizontal shift/movement in the x direction
k = Vertical shift/movement in the y direction