Solving Systems Algebraically (2 variables)
Min and Max of Objectives
Solving Systems Algebraically (3 variables)
Word problems (Chapter 3)
Matrix Operations
Multiplying Matrices
Inverse of Matrix
Solving Matrix Equations
Finding the Area of a Triangle
Factoring Quadratic Equations
100
Solve the system of linear equations
9x+y=2
-4x-y=-17
(-3,29)
100
Find the maximum and minimum values for the objective function C = 3x + 4y for the constraints
3 ≤ x ≤ 8
2 ≤ y ≤ 6
2x + y ≤ 12
Max = 37 min = 17
100
Solve this system.
x + y - 3z = 8
y - 3z = 5
z = -1
x=3
y=2
z=-1
(3, 2, -1)
100
You want to buy an aquarium and stock it with goldfish and angelfish. The pet store sells goldfish for $0.40 each and angelfish for $4.00 each. The aquarium starter kit costs $65. Write a model for the amount you will spend as a function of the number of goldfish and angelfish you buy.
C = 0.4g + 4a + 65
100
Find the sum or difference:
[(3,2), (8,-1)]+[(-2,2), (4,5)]
[(1,4), (12,4)]
100
Find the product if possible. If it not possible, label it undefined. Find QS
Q = [(5), (9)] S = [(0,-1),(4,6)]
Undefined
100
What is the inverse of
[[3,2],[4,1]]
[[-1/2,2/5],[4/5,-3/5]]
100
2A-[[4,2],[8,9]]=[[2,6],[4,5]]
[[3,4],[6,7]]
100
Find the area of a triangle with the given vertices:
A(3, 6)
B(3, 0)
C(1, 3)
6 square units
100
Solve the following quadratic equation by factoring.
2x2 - 5x - 3 = 0
x = -1/2 x = 3
200
Solve the system of linear equations
3y+4x=3
x+3y=-6
(3,-3)
200
What is the objective function for a company makes a profit of $40 on a pair of downhill skis and $30 on a pair of cross country skis
P = 40x + 30y
or
C = 40x + 30y
200
-x + y + z = 6
x - 2y + 3z = 5
-2x + y - 2z = -1
x = -2
y = 1
z = 3
(-2, 1, 3)
200
You have $25 to spend on picking 21 pounds of three different types of apples in an orchard. The Empire apples cost $1.40 per pound, the Red Delicious apples cost $1.10 per pound, and the Golden Delicious apples cost $1.30 per pound. You want twice as many Red Delicious apples as the other two kinds combined. Write a system of equations to represent the given information.
e + r + g = 21
1.4e + 1.1r + 1.3g = 25
r = 2(e + g)
200
Find the sum or difference:
[(3, -4), (1, 2), (-7,1)]-[(0,5), (-3,2), (-2,4)]
[(3, -9), (4, 0), (-5, -3)]
200
Find BD if possible. If it is not possible, label it undefined.
B=[(0,2),(-2,1),(-1,0)] D=[(1,0),(0,
[(0,2),(-2,1),(-1,0)]
200
Find the inverse of the following matrix, if possible.
[(3,4),(3,4)]
No inverse
200
What is the solution of the matrix equation
[[5,3],[2,1]][[x],[y]]=[[-5],[1]]
[[2],[-5]]
200
Find the area of a triangle with the given vertices:
A(-4, 2)
B(3, -1)
C(-2, -2)
11 square units
200
Solve the following quadratic equation by factoring:
2x2 - 8x - 10 = 0
x = 5, -1
300
Solve the system of linear equations
-5x+3y=51
y=10x-8
(3,22)
300
Vertices at (5, 0) and (4, 2) and (8,1). Find the maximum value for objective function
P = x - 2y
Maximum at 6
300
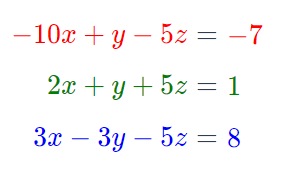
x=-1
y=-7
z=2
(-1, -7, 2)
300
You have $25 to spend on picking 21 pounds of three different types of apples in an orchard. The Empire apples cost $1.40 per pound, the Red Delicious apples cost $1.10 per pound, and the Golden Delicious apples cost $1.30 per pound. You want twice as many Red Delicious apples as the other two kinds combined. How many pounds of each type should you buy?
pick 5 lbs of Empire apples, 2 lbs of Golden Delicious apples, and 14 lbs of Red Delicious
300
Solve the following equation:
X-[(3,4),(4,2),(1,9)]=[(5,7),(9,12),(3,2)]
[(8,11),(13,14),(4,11)]
300
Find the 5D - A
D = [(1,0),(0,1)] A=[(1,-1),(3,-2)]
[(4,1),(-3,7)]
300
Find the inverse of the following matrix, if possible.
[(4,3),(3,2)]
[(-2,3),(3,-4)]
300
3A+[[1,9,12,6],[18,7,5,3]]=[[13,12,22,17],[14,15,20,10]]
[[4,1,10/3,11/3],[-4/3,8/3,15/3,7/3]]
300
Find the area of a triangle with the given vertices:
A(-3, 4)
B(6, 3)
C(2, -1)
20 square units
300
Solve the following quadratic equation:
4x2 - 17x - 15 = 0
x = 5
x = -3/4
400
Solve the system of linear equations.
3x-2y=-5
4x+5y=47
(3,7)
400
List at least 4 steps used when solving a linear programming problem.
(1) Define variables (2) Write the constraints (3)Graph the constraints (4) Identify the vertices (5) Write the objective function (6) Plug the vertices into the objective function (7) Find the max or min
400
x - 3y + 6z = 21
3x + 2y - 5z = -30
2x - 5y + 2z = -6
x = -3
y = 2
z = 5
(-3, 2, 5)
400
You are buying beads and strings to make a necklace. The strings costs $1.50, a package of 10 decorative beads costs $0.50, and a package of 25 plain beads costs $0.75. You can spend only $7.00 and you need 150 beads. How many packages of each type of bead should you buy?
Buy 5 packages of decorative beads, 4 packages of plain beads and the string for a total cost of $7.00
400
Solve the following equation:
[(-2,-3),(2,2)]=X-[(1,-1),(-2,2)]
[(-1,-4),(0,4)]
400
Find the product. If not possible, label it undefined.
[(2,-1),(5,3)][(0,4),(-3,1)]
[(3,7),(-9,23)]
400
What is the inverse matrix of the following matrix:
[[4,9],[8,5]]
[[-5/52,9/52],[2/13,-1/13]]
400
What is the solution of
[[12,-3],[16,4]][[x],[y]]=[[144],[-64]]
[[8],[4/3]]
400
Black-necked stilts are birds that live throughout Florida and surrounding areas but breed mostly in the triangular region with the following coordinates. Estimate the area of this region. The coordinates are given in miles
(35, 220)
(112, 56)
(0, 0)
11,340 mi2
400
Solve the following quadratic equation by factoring:
5n2 + 41n - 12 = -4 + 2n
{x = 1/5, -8}
500
Solve the system of linear equations.
15x-5y=-20
-3x+y=4
Infinitely Many Solutions
500
The set of inequalities in a linear programming problem are the ___________ and the solution set is the ____________.
(1) constraints
(2) feasible region
500
2x - y + 2z = 6
-x + y + z = 0
-x - 3z = -6
Infinitely Many Solutions
(6 - 3z, 6 - 4z, z) (if z is neutral)
or
(x, 4x/3 - 2 , -x/3 + 2) (if x is neutral)
500
An appliance store manager is ordering chest and upright freezers. One chest freezer costs $250 and delivers a $40 profit. one upright freezer costs $400 and delivers a $60 profit. Based on previous sales, the manager expects to sell at least 100 freezers. Total profit must be at least $4800. Find the least number of each type of freezer the manager should order to minimize costs.
Order 120 chest freezers. This will give a profit of $4800 at a cost of $30,000.
500
Find the value of each variable:
[(8,6),(-2,0)]=[(3a-1,2a),(5b+3,a+3b)]
a=3;b=-1
500
Find the product if possible. If it is not possible, label it undefined.
[(2, -1, 6)][(2),(-1),(6)]
[41]
500
Find the inverse for the following matrix:
[[10,-4],[3,2]]
[[1/4,1/2],[-3/8,5/4]]
500
What is the solution of
[[3,4,-3],[2,5,3],[-1,6,4]][[x],[y],[z]]=[[1833],[5152],[5574]]
[[236],[645],[485]]
500
On a Marconi-rigged sloop, there are two triangular sails, a mainsail, and a jib. The coordinates of the sails are given below and are measured in feet. Find the area of both the mainsail and the jib
Mainsail
(0, 2)
(12, 2)
(12, 26)
Jib
(14, 2)
(22, 2)
(14, 18)
Mainsail is 144 ft2
Jib is 64 ft2
500
Solve the following quadratic equation by factoring:
-2m2 - 60m +72 = -8m2 - 3m
{x = 3/2, 8}