Systems of Equations Word Problems
Simplifying Expressions
Factoring
Multiplying/Dividing and Addition/Subtraction
Other
100
The first integer is 4 more than the second integer. Their product is 60. Find the integers.
-10 and 6
6 and 10
100
((2x^3y^2)^4*(x^2y)^3)/(4x^5y^6)^2
x^8/y
100
4x^2+12x+3x+9
(x+3)(4x+3)
100
3/(x+2)+4/(x+3)
(7x+17)/((x+2)(x+3))
100
Write 0.00032 in scientific notation.
Write 7.2 * 10^-3 in standard notation
3.2*10^-4 and 0.0072
200
The first integer is 2 less than three times the second integer. Their product is 80. Find the integers.
5 and 13
200
((x^3y^2)/(2x^4y^3))^-2*((2x^5y^4)/(x^2y))^3
32x^11y^11
200
2x^2+5xy-3y^2
(2x-y)(x+3y)
200
x/(x+3) + (2x)/(x−2) − (x+12)/(x^2 +x−6)
(3(x^2+x-4))/((x+3)(x-2)
200
Solve the system of equations by graphing
y=2x+1 and y=-x+4
(1,3)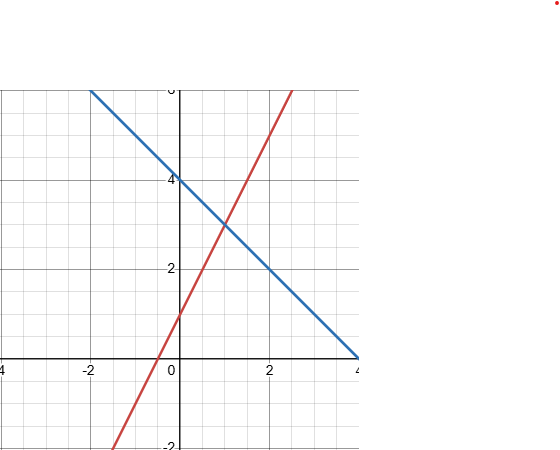
300
A baker mixes two types of flour. One type costs $1.50 per pound, and the other costs $2.00 per pound. The baker wants to mix 40 pounds of flour worth $1.75 per pound. How many pounds of each type of flour should the baker use?
20 pounds of the $1.50 per pound flour
20 pounds of the $2.00 per pound flour
300
(-4x^2)^3*(x^3)^2
-64x^12
300
3x^2-3xy-36y^2
3(x-4y)(x+3y)
300
(5x^2+13x-6)/(x+3)*(5x^2-17x+6)/(x-2)
(x-2)/(x-3)
300
Solve using synthetic division. If there is a remainder, leave the answer in quotient + remainder/divisor
(2x^3-3x^2+5x-6)/(x-2)
2x^2+x+7+8/(x-2)
400
A store sells two types of shirts. One type costs $12, and the other costs $15. The store wants to sell 120 shirts and earn a total of $1,500. How many shirts of each type should the store sell?
100 $12.00 shirts
20 $15.00 shirts
400
(3x^4y^3)^-2/(6x^2y^-1)^-3
24/(x^2y^9)
400
27x^3-125y^3
(3x-5y)(9x^2+15xy+25y^2)
400
(x^2−x−6)/(x^2 +6x−7) · (x^2+x−2)/(x^2 +2x) ÷ (x^2+7x)/(x^2 −3x)
1
400
Solve using long division. If there is a remainder, leave the answer in quotient + remainder/divisor.
(x^3-3x^2+3x-1)/(x-1)
x^2-2x+1
500
A company produces two types of gadgets. Type A costs $20 to produce, and Type B costs $30 to produce. The company wants to make 300 gadgets with a total production cost of $8,000. How many Type A and Type B gadgets should the company produce?
100 Type A gadgets
200 Type B gadgets
500
(x^3y)/z*(xz^3)/(x^2y^2)*(yz)/(xyz)
(xz^2)/y
500
x^4-1
(x-1)(x+1)(x^2+1)
500
Solve the equation and check the solution. Check for any extraneous roots.
(x+1)/(x+2)+(1)/(x^2+x-2)=1
x=2
500
Let
P(x)=x^100-2x^50+1
(a) Find the remainder when P(x) is divided by x −1.
(b) Is x−1 a factor of P(x)?
Yes, x-1 is a factor if P(x). Use the remainder theorem.