h(x) = 3x + 3 g(x) =−4x + 1
Find (h + g)(10)
-6
Rewrite "f of g of x" in TWO ways
f(g(x)) and
f o g(x)
Find the inverse of:
f(x) = 4x
f^-1(x)=x/4
Describe the transformation:
f (x) = |x - 3|+1
Describe the transformation: shifted right 3 and shifted up 1
Explain what a piecewise function is and how to graph it.
A piecewise function is a function whose domain is split into multiple intervals (boundary lines). I recommend making tables to graph each piece and paying attention to closed vs open circles!
f (x) = 4x − 3 g(x) = x^3+ 2x
Find ( f − g)(4)
-59
Find g(h(n))
g(n) = 2n + 3 h(n) = n − 1
2n+1
Find the inverse of
f(x)=1/2(x-8)
f^-1(x)=2x+8
Describe the transformation:
f (x) = 3|x + 2|+ 1
Describe the transformation: vertical stretch by factor of 3, translated left 2 and translated up 1
Give the domain and range:
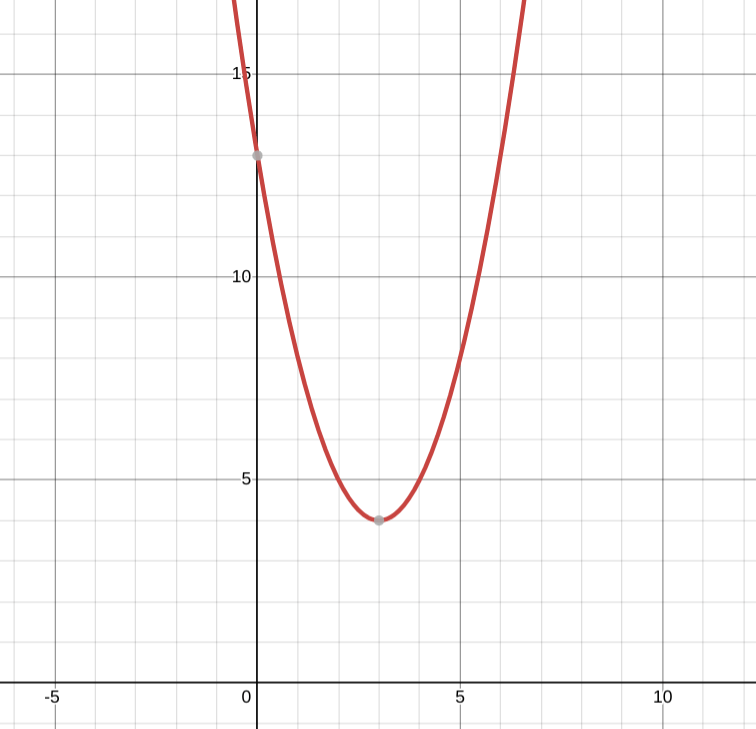
Range:
[4,infty)
Domain:
(-infty,infty)
g(a) = 2a − 1 h(a) = 3a − 3
Find (g ⋅ h)(−4)
135
Find h (g(x))
h(x) = x^2 − 2 g(x) = 4x + 1
16x2 + 8x − 1
Find the inverse of:
g(x) = (7x+18)/2
g^-1(x)=(2x-18)/7
Describe the transformation:
f(x)=1/2|x+4|+4
Describe the transformation: vertical shrink by half, shifted left 4 and shifted up 4
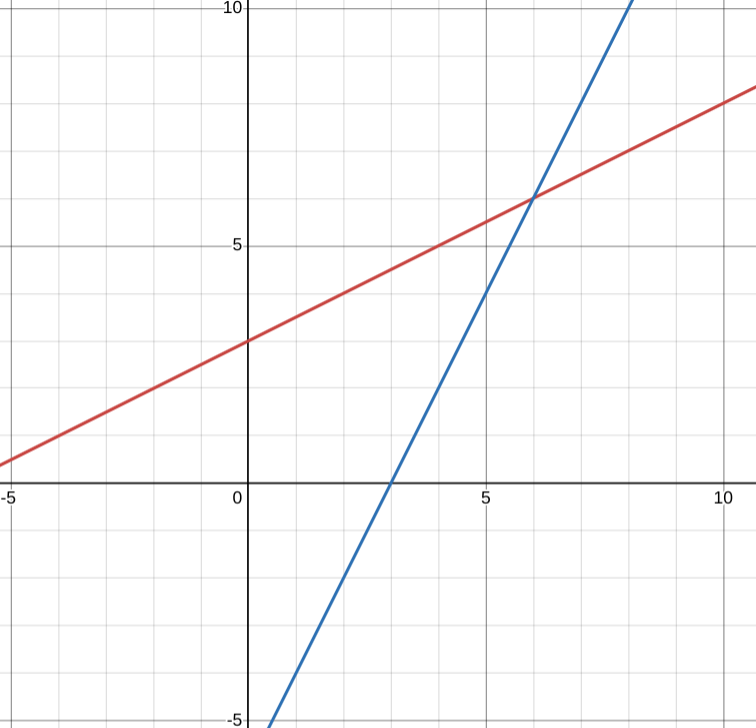
Graph the function and its inverse on the same coordinate plane:
f(x)=1/2x+3
f (x) = 3x − 1 g(x) = x− 4
Find
(f/g)(x)
(3x-1)/(x-4); x ne4
Find g (f (−2))
g(x) = 2x − 2 f(x) = x^2 + 3x
-6
Find the inverse of:
h(x) = (√x) -3
h^-1(x)=(x+3)^2
Describe AND graph the transformation:
f (x) = -|x - 2|
Describe the transformation: reflected over x-axis shifted right 2
Determine if the following are inverses:
f(x)=1/2x-4
g(x)=2x+8
Yes, they are inverses
Come up with 2 functions so that
(f+g)(x) =-4x+7
Answers may vary
f(x)=3x g(x) = 2x + 2 h(x) = −2x − 5
Find:
(g-(h ⋅ f))(2)
60
Find the inverse of:
g(x)=1/(x+3)
g^-1(x)=1/x-3
Describe AND graph the transformation:
f (x) = 2|x - 4|+2
Describe the transformation: vertical stretch by factor of 2, translated right 4 and translated up 2