Graphs
Equations
Tables
Contexts
100
f(x)=6, x =
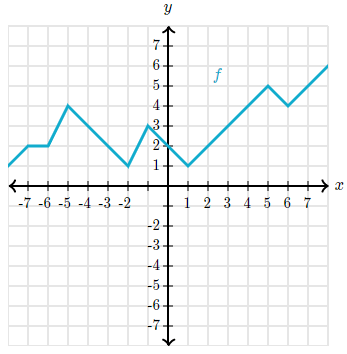
The output (y) is 6, so the input is 8.
100
Using the equations below, evaluate g(3).
You plug in 3 for the x (input), so
g(3) = 2(3) + 1
= 7
100
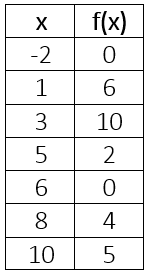
Evaluate f(10) =
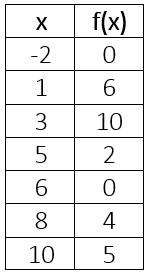
10 is the input, so the output is 5.
100
Mendy wanted a moped. She had $250 saved already, but then she made $45 a day tutoring. Her equation was M(x)=250 + 45x.
Translate M(3).
How much money would Mendy have after 3 days of tutoring?
200
f(-4) =
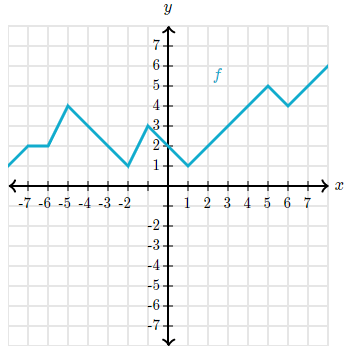
The input (x) is 4, so the output is 3.
200
Using the equations below, evaluate h(0).
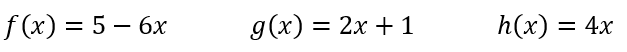
You plug in 0 for x (input) into the "h(x)" equation, so
h(0) = 4(0)
= 0
200
Evaluate f(x) = 4, x =
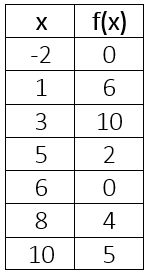
4 is the output, so the input is 8
200
Mendy wanted a moped. She had $250 saved already, but then she made $45 a day tutoring. Her equation was M(x)=250 + 45x.
Translate M(x) = 430.
If Mendy has $430, how many days has she been tutoring?
300
f(x) = 2, so x =
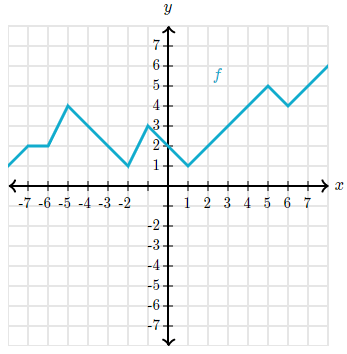
The output (y) is 2, so the input is 0.
300
Given the functions below, evaluate f(x) = 23, x =
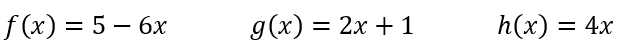
It's telling you that the output is 23, so plug in 23 for f(x), and you get
23 = 5 - 6x
-5 -5
___________
28 = -6x
x = -3
300
Evaluate f(x) = 5, x =
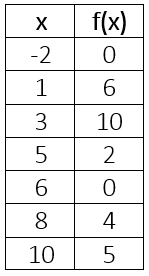
5 is the output (y), so the input is 10.
300
Mendy wanted a moped. She had $250 saved already, but then she made $45 a day tutoring. Her equation was M(x)=250 + 45x.
Evaluate M(5).
That's 5 days of tutoring, so in your table you can look or plug 5 into the equation, so
M(5) = 250 + 45(5) = 475 dollars
400
f(x) = -1, x =
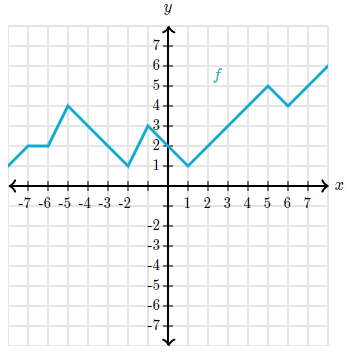
Does not exist! There's no graph there!
400
Use the equations to find a new one and call it P(x).
P(x) = f(x) + g(x)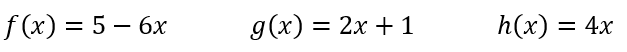
You add the starting points and the rates of change, so you'd get
P(x) = 6 + -4x or
P(x) = 6 - 4x or
P(x) = -4x + 6
400
Evaluate f(1) =
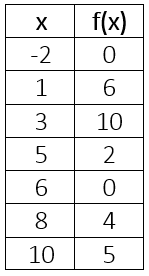
1 is the input, so 6 is the output.
400
Mendy wanted a moped. She had $250 saved already, but then she made $45 a day tutoring. Her equation was M(x)=250 + 45x.
Write the function notation that would go with this question: "How much money did Mendy have after 12 days?"
12 days is the input, so
M(12)
500
f(x) = 5, x =
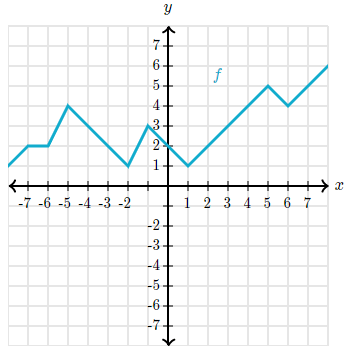
When the output (y) is 5, then the input is 5 AND 7.
500
Let M(x) = f(x) + h(x)
Evaluate M(3).
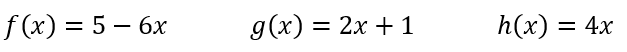
You have to add the two equations first, so you'd get
M(x) = -2x + 5
So M(3) would be
M(3) = -2(3) + 5 = -1
500
Evaluate f(x) = 0, x =
When 0 is the output, then the input is -2 AND 6.
500
Mendy wanted a moped. She had $250 saved already, but then she made $45 a day tutoring. Her equation was M(x)=250 + 45x.
Write the function notation that would go with this question: "If Mendy had $1150, how many days had she been tutoring?"
$1150 is the output, so
M(x) = 1150, x =