Important to Know
Naming Functions
Evaluating Functions
Function Notation Vs Not
Walking Through a Word Problem
100
What is a relationship between an independent & dependent variable?
a function
100
How would you write: "the function f of x"?
f(x)
100
Evaluate the function f(x) = 2x at 2.
(This means the input = 2)
f(2) = 2(2)
f(2) = 4
100
Rewrite y = 2x + 10 as a function named f.
f(x) = 2x + 10
100
The height [f(x)] in inches of a plant depends on the amount of water (x) it receives in Liters.
The plant is already 2 inches tall and grows 2 inches per L.
Identify the IV(input) & DP(output) here.
IV = x-amount of water
DV = f(x)-height of plant
200
Which variable depends on our input? (often written as y or f(x))
Which variable does not depend on anything else? (often written as x)
Write answer in correct order :)
1. Dependent Variable (output)
2. Independent Variable (input)
200
How would you write : "The function g of t"?
g(t)
200
Evaluate the function f(x) = 5x + 10 at 4.
(The input is 4.)
f(4) = 5(4) + 10
f(4) = 30
200
Rewrite y = 2x + 1 as a function named g.
g(x) = 2x + 1
200
The height [f(x)] in inches of a plant depends on the amount of water (x) it receives in Liters.
The plant is already 2 inches tall and grows 2 inches per L.
True or False: Our function would look like this:
f(x) = 2x + 2
True
300
What variable (letter) can we think of f(x) as being?
OR
What can we replace f(x) with in our minds?
y
300
What is our input variable in "the function f of x"?
x
300
Evaluate the function f(t) = 2t + 10 at 2.
(the input = 2)
f(2) = 2(2) + 10
f(2) = 14
300
Rewrite y = 2h + 2 as a function named f.
f(h) = 2h + 2
300
The height [f(x)] in inches of a plant depends on the amount of water (x) it receives in Liters.
The plant is already 2 inches tall and grows 2 inches per L.
Our function is f(x) = 2x + 2. Evaluate the height of our plant at x=3. (It's had 3L of water)
f(3) = 2(3) + 2
f(3) = 8 inches
400
Which represent our output and input?
f(x) : ?
x : ?
f(x) : output
x : input
400
How would we write : "The function g of h is equal to 2 times the input variable"?
g(h) = 2h
400
Evaluate the function g(h) = 2x + 2x + 1 at 0.
input = 0
g(0) = 2(0) + 2(0) + 1
g(0) = 1
400
Rewrite f(h) = 2h + 1 using "y" for our output variable.
y = 2h + 1
400
Evaluate our function using the graph at x=1.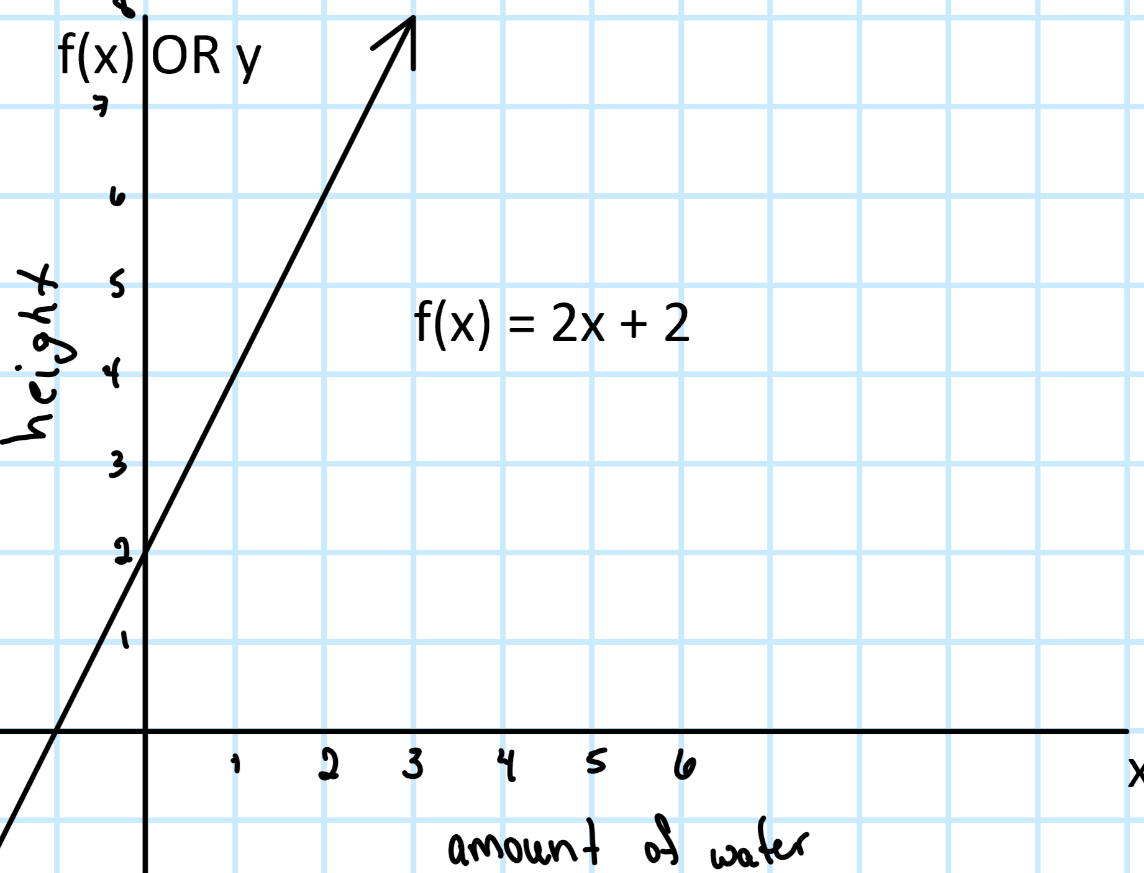
f(1) = 4 inches
500
Which represents our output and input?
g(h) : ?
h : ?
g(h) : output
h : input
500
How would we write : "The function g of t is equal to 5 times the input variable plus 2"?
g(t) = 5t + 2
500
Evaluate the function h(t) = 2t + t at 1.
Input = 1
h(1) = 2(1) + (1)
h(1) = 3
500
Rewrite g = 2h + 1 as a function named z.
z(h) = 2h + 1
500
Using our graph: Evaluate our function at x = 0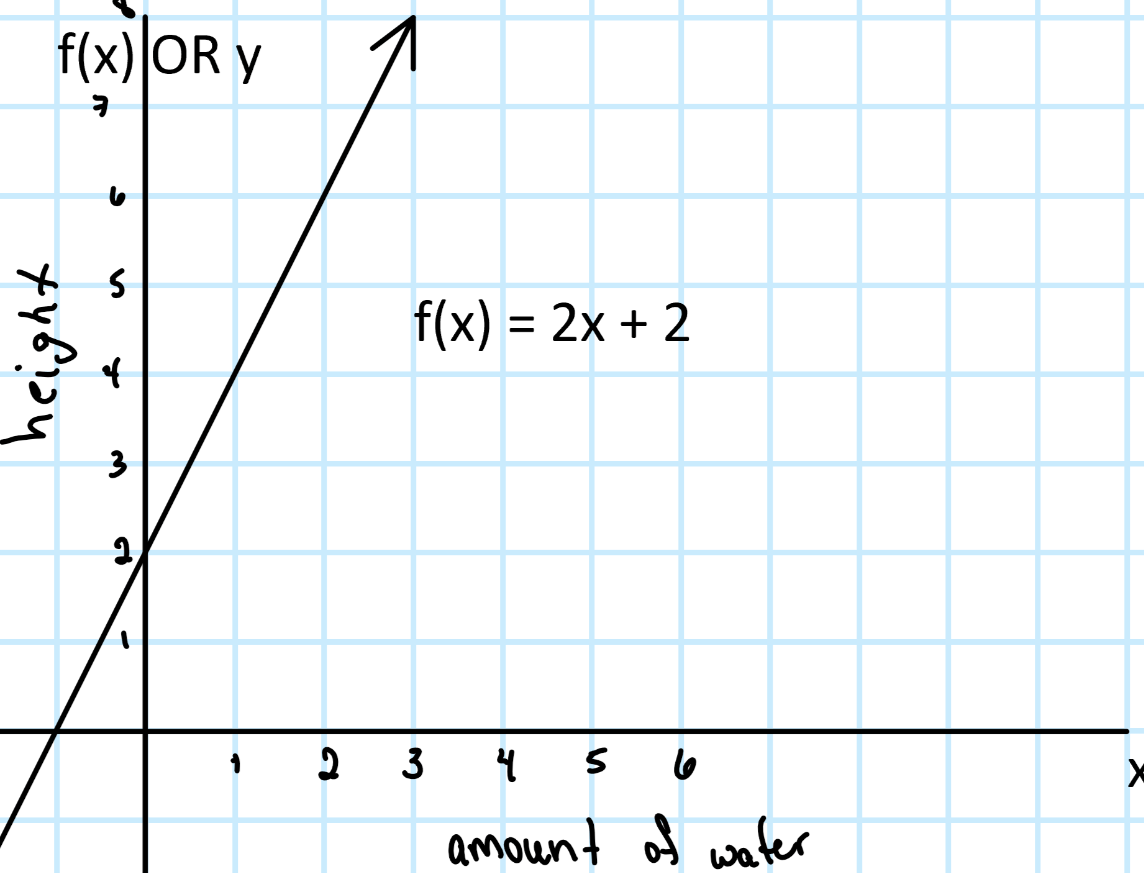
f(0) = 2