What is a relation?
A set of input and output values.
State the domain and range:
| x | y |
| 3 | 7 |
| 5 | 9 |
| 3 | 8 |
D: {3, 5}
R: {7, 8, 9}
Is it a function? Justify your answer. {(2, 3), (4, 5), ( -2, 6)}
If the relation is a function. Determine if it's linear or nonlinear. Justify your answer.
Yes, it's a function because each input has exactly one output (all x-values are different).
It's a nonlinear function because it does not have a constant rate of change.
What is the y-intercept?
The y-coordinate of the point where a graph crosses the y-axis.
State the domain and range: 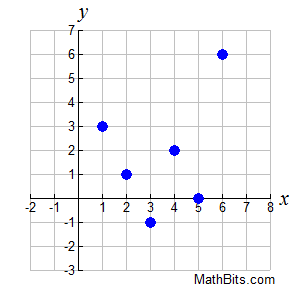
D: {1, 2, 3, 4, 5, 6}
R: {-1, 0, 1, 2, 3, 6}
Using the vertical line test, does the graph of the points (1,3) and (1,5) represent a function?
No, the points fail the Vertical Line Test.
What test determines if a graph is a function?
Vertical Line Test
State the domain and range: 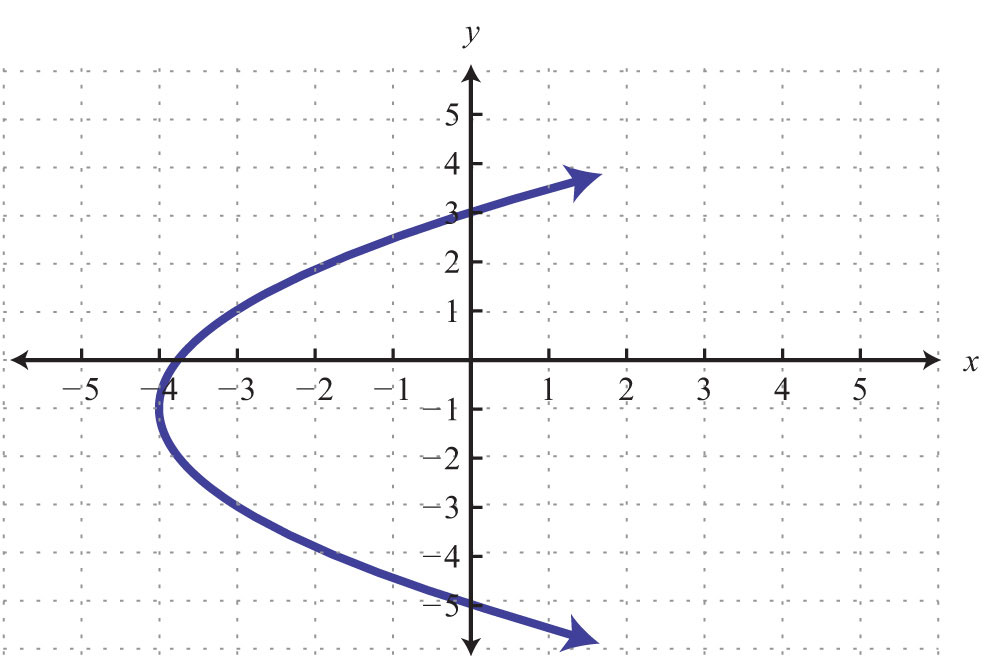
D: [-4, infinity)
R: (- infinity, + infinity)
Is it a function? Justify your answer. If it's a function, determine if it's linear or nonlinear; justify your answer.
| x | y |
| 2 | 4 |
| 1 | 5 |
| 2 | 6 |
No, the relation is not a function because the input of 2 has two different outputs (not all x-values are different).
When is a function positive?
When the graph lies above the x-axis.
For f(x)=-2x+9, find the value of f(4)+3.
4
State the domain and range: y=3x + 9
D: (- infinity, + infinity)
R: (- infinity, + infinity)
Is it a function? Justify your answer. If it's a function, determine if it's linear or nonlinear; justify your answer.
7x+2y=14
It's a linear function because it is written in standard form and makes a non-vertical line when graphed.
What is a function?
A relation in which each input has exactly one output.
For f(x)=-3x+2, find the value of f(3) - f(6).
9
State the domain and range:
{(-11, 2), (-9, 2), (-7, 3), (-5, 3), (-3, 3)}
D: {-11, -9, -7, -5, -3}
R: {2, 3}
Is it a function? Justify your answer. If it's a function, determine if it's linear or nonlinear; justify your answer. 
Yes, it's a function because each input has exactly one output; passes the VLT.
It's a nonlinear function because it's not a line.