Using Function Notation
Inverse Functions
One-to-One Functions
Domain and Range of Functions
100
VH
f(x)=2x-2
find f(7)
=12
100
SN
What is the inverse when x=3? 
(7, 3)
100
RD
is f(x)=x2+4x+3 a one-to-one function?
no
100
RD
What is the domain and range of the function?
range: [0, ∞ )
domain; (-∞ , ∞ )
200
SN
if f(x)= 3x-12
find f(-4)
-24
200
VH
Will the inverse of this function also be a function? Why or why not?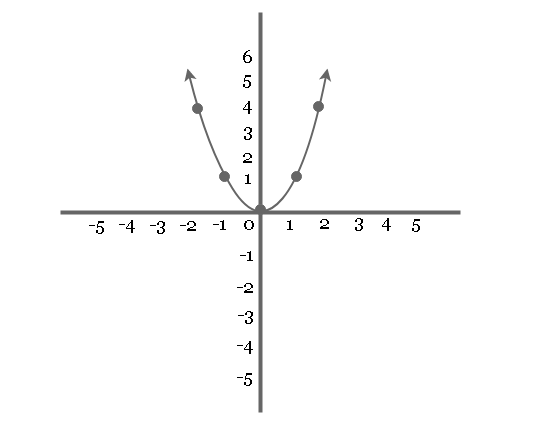
No, the inverse will not be a function because it does not pass the vertical line test.
200
SN
is the graph a one to one function?
no
200
CC
what is the domain and range of the table?
domain: [1,5]
range: [3,11]
300
CC
what is f(-1)?
-4
300
CC
If f(5) = -8, what point must lie on the graph of this function's inverse?
(-8, 5)
300
VH
do the points on this table make up a one-to-one function?
yes
300
SN
what is the domain and range of y=-3x+4?
all real numbers
400
CC
What input makes f(x)=g(x)
x=5
400
RD
f(x) = 2/3x-2
Find f⁻¹(2).
f⁻¹(2) = 6
400
CC
which of the following equations is a one-to-one function?
a.) x2-2x+1=y
b.) x2+3=y
c.) 2x2-3x-2=y
d.) 2x+3=y
d.) 2x+3=y
400
VH
which of the following values of x would not be in the function y = √ x+6
a.) -4
b.) -7
c.) 4
d.) -6
b.) -7
500
RD
what is f(g(x)) when f(x) = x2 and g(x) = x+3
x2+6x+9
500
RD
g(x) = x² + 7x -3
Find the inverse when x=4.
(41, 4)
500
VH
which of the following equations is not a one-to-one function?
a.) x2+x-1=y
b.) 3x+1=y
c.) x2+4x-2=y
d.) 3x=y
d.) x2+4x-2=y
500
SN
which of the following values of x would not be in the domain of the function defined by f(x)=x+4/x-4
x=4