Domain/Range
Independent/Dependent
Independent/Dependent
Is it a Function?
Function Notation
Function Notation
Operations and Context
Operations and Context
Function Notation
Tables and Graphs
Tables and Graphs
100
What is the domain?
{ (1,-2) , (5,2) , (-1,4) , (5,0) }
{-1,1,5}
100
Is it a function?
{(2, 3), (4, 5), ( -2, 6), (-4,3)}
Why or why not
YES because x does not repeat
100
Evaluate h(x) = 3.7x - 15.4
Find h(1/2)
-13.55
100
f(x) = 8x + 3 and g(x) = -4x - 7
Find f(4) - g(-6)
18
100
What is f(-1)?
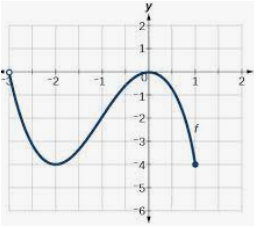
-2
200
What is the range?
{-2,2,4}
200
Is this a function? Why or why not.
No, it fails the vertical line test
200
Find f(-6)
f(x)=2/3x-4
-8
200
h(a) = 6x2 - 2x
Find 12[h(-4)]
1248
200
What is f(2)?
4
300
What is the domain?
{2,4,8,9}
300
Is it a function? Why or why not.
Yes, the input values (x) do not repeat
300
g(x) = x2 + 4x
find g(-2)
-4
300
Find
f(-1)/(h(2))
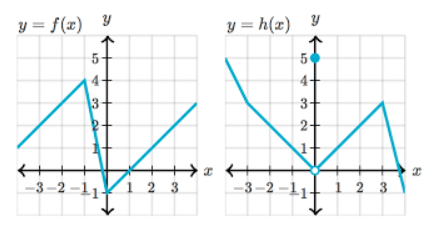
2
300
State an interval that is decreasing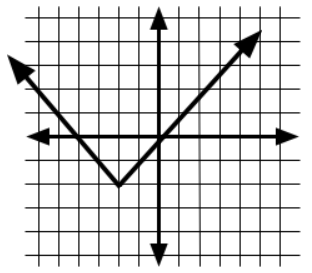
x = (- infinity, -2]
or x < = to -2
400
State the domain of the function:
3x + 6 < 12
{ x is a real number | x<2} or
x= (-infinity, 2]
400
Is it a function? Why or why not?
Yes, each x is only used once
400
h(m)= 5.2m - 7.1
If h(m) = 25.4, what is m?
6.25
400
Find
g(2) *h(2)
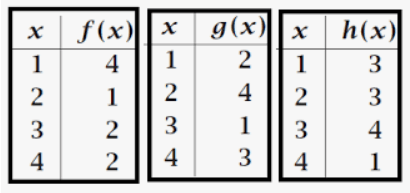
12
400
If f(x) = 2, what is x?
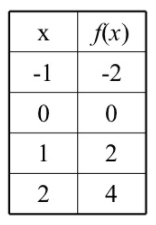
1
500
state the Range of the function shown in the graph
y greater than or equal to -3
or y = [-3, infinity)
500
Name a point that would make this graph NOT a function.
Answers will vary, but the x-coordinate must be one of the following:
1,2,3,4,5,6
500
Evaluate for the domain {-4,1,8}.
f(a)=(5a^2-a)/16
{.25, 5.25, 19.5}
500
The function D(m) represents a runner's distance from home in miles after m minutes. What is the meaning of D(23) = 6?
The runner is 6 miles from home after 23 minutes.
500
If f(x) = 3, what is x?
-1 and -3