What are the range and domain of a function?
Range: All the outputs (y-values)
Domain: All the inputs (x-values)
What are the 4 types of ways to represent a function?
Graph
Verbal
Table
Equation (function rule)
What does a linear function look like? A nonlinear function?
Linear-- a straight line
Nonlinear--not a straight line
A cup of hot chocolate's temperature decreases at a constant rate. Which graph best represents this situation?
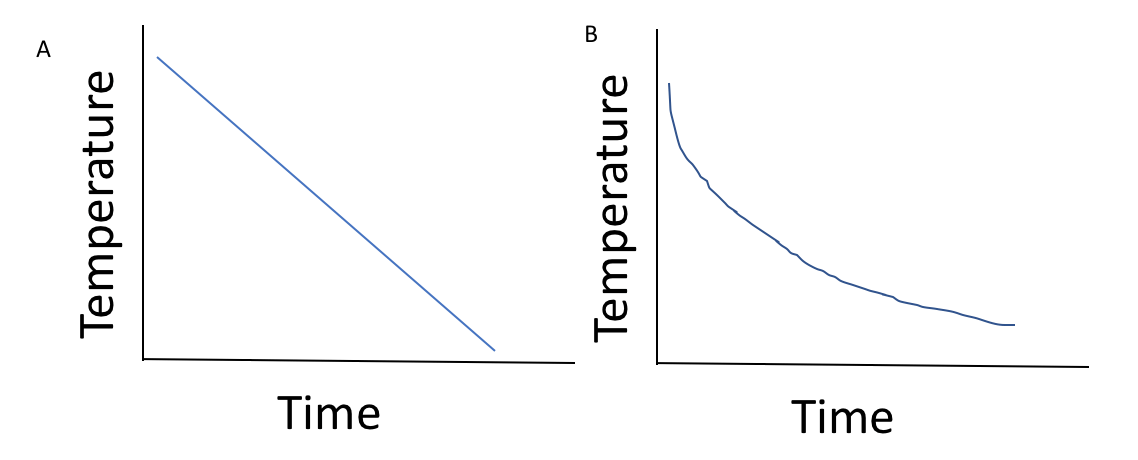
Graph A
List the ordered pairs from this mapping diagram:

(-1, 5) (0,3) (1,5) (2,11) (3,21)
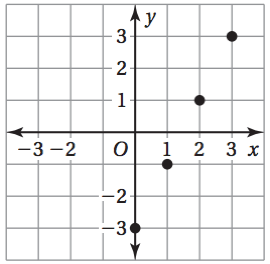 Write the linear function for this graph
Write the linear function for this graph
y = 2x - 3
Which are linear functions and which are nonlinear?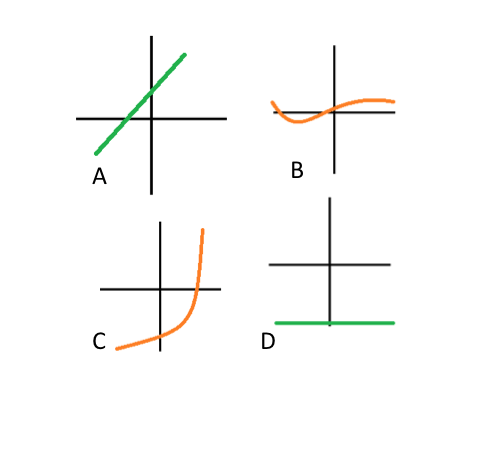
linear: A, D
Nonlinear: B, C
Is this a variable slope or constant? Is the function linear or nonlinear?
<img data-fr-image-pasted="true" src="data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAuQAAAMECAYAAAD3lzBTAAAgAElEQVR4Aey9Z5Nc15Wmu9JUlncoeG8IAiToSVFSS5TU3VL3fJrpiTsRN+bf9D+a+2HuRMed0UgaGTZJkRQ9CMITHijvTWbeeNY5K+tUIisrYYpVlfUe9cFx2z67mvHulWuvnatWq1XTIQIiIAIiIAIiIAIiIAIisCUE8ltSqyoVAREQAREQAREQAREQARFwAhLk+kMQAREQAREQAREQAREQgS0kIEG+hfBVtQiIgAiIgAiIgAiIgAhIkOtvQAREQAREQAREQAREQAS2kIAE+RbCV9UiIAIiIAIiIAIiIAIiIEGuvwEREAEREAEREAEREAER2EICEuRbCF9Vi4AIiIAIiIAIiIAIiIAEuf4GREAEREAEREAEREAERGALCUiQbyF8VS0CIiACIiACIiACIiACEuT6GxABERABERABERABERCBLSQgQb6F8FW1CIiACIiACIiACIiACEiQ629ABERABERABERABERABLaQgAT5FsJX1SIgAiIgAiIgAiIgAiIgQa6/AREQAREQAREQAREQARHYQgIS5FsIX1WLgAiIgAiIgAiIgAiIgAS5/gZEQAREQAREQAREQAREYAsJSJBvIXxVLQIiIAIiIAIiIAIiIAIS5PobEAEREAEREAEREAEREIEtJCBBvoXwVbUIiIAIiIAIiIAIiIAISJDrb0AEREAEREAEREAEREAEtpCABPkWwlfVIiACIiACIiACIiACIiBBrr8BERABERABERABERABEdhCAhLkWwhfVYuACIiACIiACIiACIiABLn+BkRABERABERABERABERgCwlIkG8hfFUtAiIgAiIgAiIgAiIgAhLk+hsQAREQAREQAREQAREQgS0kIEG+hfBVtQiIgAiIgAiIgAiIgAhIkOtvQAREQAREQAREQAREQAS2kIAE+RbCV9UiIAIiIAIiIAIiIAIiIEGuvwEREAEREAEREAEREAER2EICEuRbCF9Vi4AIiIAIiIAIiIAIiIAEuf4GREAEREAEREAEREAERGALCUiQbyF8VS0CIiACIiACIiACIiACRSEQAREQARF4MgLVarWWgftcLld7jpvs+0bfI52uIiACIiACIiBBrr8BERABEXhCAsvLy1Yul41rpVKxYrHoohwRzsk7jlKpZB3FohXS709YjZKLgAiIgAjsEgIS5LtkoNVNERCBpyeA+EZkr6ysuBCfnZmxpaUlm5+ft3KlYqWOjkSQm1m1UnGhns/nrbu7u3YWOzpcuPOeU4cIiIAIiIAIBAEJ8iChqwiIgAg0IIAQf/TokU1NTtqVK1dsbHTUHjx4YHNzc4mFvFq1Qj5fc1vBQo6Az+dyhggfGhqykZERO3zkiB05etT27NljAwMDVigUGtSmVyIgAiIgAruRgAT5bhx19VkERKApgXA9wQq+uLho39+8aXfv3rW//OlPdvPmTbt544bNzM4anuO5fL5m+abQsKRjKaecvXv32uHDh+2lCxfstTfesJMnT7p47+npWZOvaYP0UQREQAREoK0JSJC39fCqcyIgAk9DYHFhwRYWFuzzL76wG9ev25XvvrPRR4/s6rVrNjE+bhMTE+6+0j8wYH19fXbmzBm/VqpVm5mZsWtXrtjk5KTNzc+7NX1hcdFm5+bs9u3bduLECTt56pSdPnXKTp05Y/39/S7Mn6adyiMCIiACItAeBCTI22Mc1QsREIHnQADrNidiemxszP79/fft048/tuvXrxt+476IM3VRwT/84MGDtnffPvvpz35me0dGPO/DR4/cj/zO7dvGPcL+4YMHLui/vXjRjhw5YqdOn7bJd96xru5uKx4/bljL5cLyHAZQRYiACIjADiUgQb5DB07NFgEReL4EcC/Buj01NWV//MMf7JtvvrEvvvjC7t654wIdMW7VqkdOeeHsWTt46JC9/fbb7o6CwEZUYyGfnZ21w4cO2e1bt+zTTz6xy5cv2527d30RKC2+f/++u8FgMf/+1i379T/9k5178UUbHBqyjnRx6PPtmUoTAREQARHY7gQkyLf7CKl9IiACPwgBLOMP7t+377//3v7whz/Yhx984OK6Ui5bRB3Hit3d02MXXnnFzp0/b7/4xS/s0KFDVursrC3qpJyzZ8/ag3v3PMIKz+Pj47ayvOw+5Yh+RPuj0VG7+M03vsizs1Sy06dP29DwsCzlP8hoqxIREAER2F4EJMi313ioNSIgAltAgKgoLN785uuv7W+ffuqLNj2k4cpKrTWEKsQKvmd42F566SV77bXXfMFmZ1fXmjCGEdZwz9699vqbb9qDhw/tu+++8/JZJBoLRqmPer/4/HNbXllxy3tPb691dXXVxH2tct2IgAiIgAi0NQEFw23r4VXnREAEWiGAUMZyjXDGzQRLeTkjxikjXyjY8PCwHTp82Bdxnk4XcjaKKc673t5eIw3uLPsPHLDevr41wh3LO/Ve/u47+/ijj+zWrVseShGRrkMEREAERGB3EZCFfHeNt3orAiLQgABRUxDhhDa8T4zx+Xm3ZGeT4t99/vx5O/vii7bvwAFfkEnIw/UORDkLPwl5eOHVV33B57dzc76ZUC1PtWpj4+Pue46vOos/cV/BUt5I6Nfy6UYEREAERKCtCEiQt9VwqjMiIAJPSgAXEkIaEkkFUc4GQMupa0m2LAT5qVOn7KWXX/bNforFYlPXklwu54s0iUN+7tw5G3340K5eubJWkJvZ3Oysi/V79+75AlL8yPFTb3TQVhaXYkXHJ50rC0l5Hwf1silRoVj0DYvYnAjf92wUl3Cb4YqPOyf3lMfVo8lUKu4+UyqVamEZ2amUtNGGSE/dUSdcyMOEotGkgvI5snXX2lCpJH2qVLz9xULB/fMph7o4w9WHe/qKiw91Mj6N6qMu2u3n8rK7B3l/K5Vk/HK5hB/Rc2BGnWmfuacO2prlQpm83+ggD22ifVyzZfn4VSpeRLOyol/N0mzUDn0XARHY/gQkyLf/GKmFIiACm0QghOj1a9fss08/9ZjhCDeEVP2BoNozMmIHsI5nFnHWp6t/Jk45oQ7ZrTMriiMddVHnnTt37Ntvv/VQiuzmWZ+WtpKOXUKnp6ft/t27vjgUaz7vOUIUIyiHh4Y8Nvr+gwd9Z1BcaEKwImZxl/FzcdFdZRC6LDb1MI0PH/rEgcWp7DBKexCVxGDHtYfJA23gRJzTByz7w3v2+GTl+IkT1tfb68K2/lcE6qa9THoWl5Zsfm7O20HdtIFfK4gDz8SEXU6J284EZXJiwqZnZoyxivvOzk53CSLkJFFvEOfZg3bhGsQka3R01B4+fOiTLpgtLS4mQrlQ8PaQlvqIC3/06FF3T6IN9DtYMXFjbQHHRgKZ8jgZf8qhbYhreFEe7WEy1qwsJggH9u/3/tOOjer0wvSPCIjAjiQgQb4jh02NFgEReB4EEEwIRMTwd99+a+NjY24Bri8bcYzgRFghyhG8rR4sBEXEE9awXmRHGYhtwiQi2C5cuGDHT570ewQYAg6hio/5xNiYXbtxw9t559YtF8TsGJoV5Ag3FpqO7NljA4OD7jKDL/uZF15wFxrKRFDfvH7dxTVlI7IR4ghsBOe9u3ddpD96+NAjxuA3T9uvXr3qvyYQiQaRS7x2xCXTF8QxMdkRxy+++KIdOHjQCA+JIKVNHPAm7OONGzdsemrK60CU0oaom/jvtIXNlo4eO+Y7ocLw0rffeuSaby9dsrHRUZuanvb+sMCWXy6IBc+kh7qoh3YhwJm4+K8Pd++6S9K9O3d8l1XqJC39WuGXhkrF8w8ODNiJU6ds//79HkmHiQ3CmDaxvuD+vXv+q8SG4pjJQLXqExrY8zdA++BL+1nMi5uSW/rXcX3C5endd9/1yQabUPH3oUMERKA9CUiQt+e4qlciIAItEEC4IcQQZwglhC3v1hy5nItNxBGWWjbzQaBtKMjSQhB95EOw1luLo55qpeIWUwTX5NSUi3DahUV7bm7Ov/1///ZvdvnSJY9pjgjHsozbQ7SZVuNEQR2ITCYNlNfd1WU//bu/83smE7Tnk48/tn/7H//DhSH1EOWFq5eHW8jCgj/zDtFIPmKwf/XVVy5yY5MkJgukoe5CPl/j9Mlf/2onT5+2//u//lc7eeKEL3AlDW1lc6T/97//dxfJ9MHLKJe9DWG5h607hOAWklqaf//739v3N27YRDoJoK0dpVLN9/9MKv5dYK+suDWffv7h97/3PhBfHpYL8/M19xevJ1xSzOxmyuzTTz/1Rbi/+c1v3AJ/5OhRb+df/vxnj8SDgG/pqFbt/Esv+aZShMocGBjwyQ+Tq7/85S/29VdfuaXe1nF/YUKF1R63o3DNafXvrqX2KZEIiMC2ISBBvm2GQg0RARH4oQl4pJPUZQN3CMRh/YEAwt1jcHDQwx4irMP1oz5to2cX5F1dnrcX14tSyevJCn/EKuIUizOCEeHqQrda9RCMN65ft08++SSx4o+Pe37ENqL7+PHjLh6pB6GI5RnBjHV4YXHRBS1uJ5RNP6yry/PjtsFOoli6sf4ihrMHfcQiTgx1rNyIRiy7tJO8uJyQj7ZmDwQxIn58YsJePHfOWPZ6+oUXfEJAn4leg+DH7QQXEISyW9kzEyEmPFjR6Q8WacT3F5995iI+2076DC8i2CC2GT8mVvSV9B998IFHsME9hEkXY0m0HCzVR3E9Sl1c+EUAVxmPF59OyuCLGCYv7WBiwy8P/B1gccdCj1WftjU6SBcWe8qirUwymLgwbn09PT4eMKBu2g4fYtrzN3b0yBEbGhz0OmG6nmhvVLfeiYAI7DwChX/913/9153XbLVYBERABJ6dAIISUeU7c371lc3OzbkQzpaMMGXnTdw2fvLTn/pGQAisJ7FUUsat77+3K+miTsRhVpBTFlZQhNqbb7/tftOIRcTu7/73/7a/fvihW2YRxAg3ykMk4yLyf/2X/2L/+Otf289+/nN7/bXXXAQiUHENQaRiYcZl5ZVXX3Ufb3ykEXcITIQe4r2RIIcBdWGNRzCSDvF/7PhxK3V0uMCeR5A3EKRubV9ZsRncSnp67MTJky5+6SfWeAQnvzTwy4BbrRcW1vCgzQhtxOqd27d9R1PciWhP9oADYwGHH//kJy6gcb+5dvWq/T//7b/Zx3/9qwvqEPyIYri++dZb9h//5V/sF7/8pb311ls+IYh2hDBmkjQ7Pe0bOCGMyXf+3DnnyDf66AuA69oU7XvhhRfs5++9Z+/++Mf2xptv+t8Pv7LQ3r7+fv/VAf94fhFhchJ9ww//4MGD9h//83+2f/iHf7CXLlzwMaV++qtDBESgPQnIQt6e46peiYAItECgnC6URCBjTa639lIEIhJRiYhCMCNin0iMFwouthGhLsjSCCRZSy/1IPCyJyKSdl29fLkmxkPIIywpC//mly9c8BOBjnUYX3VOJgC0EwtvHEQtQdgdOXzYF4AyKRgfHXU3CurLtolvYQFHII7s3Wuvvvaa7du/3/AtRyDjwoK1mMWe5OcgHxZlhDGLVNmBlIkE9cJg3759LmrhiP84+bGmW8ZCTxlYzpkswRwhGqI6+tLoSnuvXbvmvGgbriEwjYM1ACzYZFOnt995x4UvfWbyQvlMMLD+k4fJAr8ysNj0u0uXvIhf//rXLqSZpHDg9+/3Get+1MWkiF8mjhw7VhPjfAsO/DrDwldcV0JoY73HPQYx/9bbb/uVXzXcQh4F6yoCItCWBCTI23JY1SkREIFWCCBYQww1S48AxrJJWvI8iSBvVu6631IxjIUZlw3ioyM2Eap+pOH+EGtMFnBzQMxhdUYAI2Jvf/+9iz/8qOMgDf1AXCMYcW9BuFM+AjgryCMPIvqdd9/1hZqIWMI4Il5x2cCa+9WXX9pnn33mFt5a+/AXJ7rJ1JRPCOhDWPTxo6ZMxDaLQ2kz0WEaHfAmPW3GnWQNg7oMlIAVn2g5X3/9tfct2x6SE+0Gqzg7qOJOgjimzyw+Jb/HoU9dZKJ4LNcIcur+0Y9+5ItVWbRKlJYPP/zQcg8euA99pI8r5TLJC4t7vI+/H74zwcJ9J9Yv4BNPiEys/YcOHfJJVyt/n1G2riIgAjuXgAT5zh07tVwEROAZCbiwblFgb7oIr+sL1nqELxZarM1Z6z1C07/NzbmFGV9nRDZCF+s4Fl7ipSP6WDgYCyOpAmsrAtct7Hv2uE80gr7+oL+kQYAT+QWXFyy3LDTkGy4eWNdp1+XLl919IyuAsTAjWlmEidDds3evW5fDQkwoRUQxrjON2DJ5oP5z58972EUEOXW6z3n6awYTj5F9+zzKCn2H1ZXLlz3eO2nT6Uuta3CiDwhzIrfErx3spAor/L7rBTDv2bCJNvqC0uVlj8CC+87+ffucgfuS1/nSM2ZEwiGdx7Xv7l7TT74TUYY248ZDX4ikcvzYMY9sg5uM+52vM1mpdUo3IiACbUFAgrwthlGdEAER2EwCiDJ8pbOCczPr26hs3B0Qc4jhjz780H218YtGlGOJdkv5mTNueWUhIk4b7oZRt4lQs3qI1oJgJqb4qdOn3Q+cHURDPCPqWayJsPwdi0XXEY5zCNO7d919o3zyZK1K2oVA5hpl1j7mcu6nzvf3fvELF+X0FZGNGwwuMFjDEewvnj/vYQH5tYDFmbifsMETIpiJSPagzbgekS/q5Io4R4wzMYn3kY/Qhbiy0E8Wi/Krgocw3LfPxTa/Yly7ft3Ks7Nr/j5wFfryyy+9bfip84tETAAom/HjFwLEPAcTKWKOswtshNasb0u0SVcREIH2IyBB3n5jqh6JgAg8ZwJYe0PQPuein6o4Jga4OTBRYMEnvsw3b950/2z8lhHlnIcPH7Z//g//wd0f2DgH4VlvAV6vAYhBRCSWbE4EKxbbOBCXxOrGR3rf3r1uRUacZi35pEXI4j5z6uTJmvsGZZMfMe5l1ol5XFiwxNNmIrVgnScdIhvrNsKYaC8IaF9kWiq5QB8bH/dvsyzOzfikR5txH0HIR7x5Ip4guHlGQFMmz2uOdOOmJeLBLyz4LxO0ZXh42H33Sf/g4UOfLGQnAAj3m8vLdvv2bS+byQyTBvjzt8R7YqtTNwcTH1xh6B9jxy8EOkRABHYPgdX/uu6ePqunIiACIrCGQJ0EW/Ntqx7cOoo7TWxBj2itE4sIzKtXrril9bO//c2trPggs6FORFz5T//yL+6HjQUWtw6EcKsHaYn+Qhtoj7cpzYywpLz+NNoL1nR8opkkZH9JYOIQ4Q3rxfp67aA+osHgLoOIpR5cOtwifu6c14GopT28R0g/vH/fo5V4HXWcoh7cQwjJyNE3Our9QrizeJM24hbTSMhH/to1dedhwx98yz2ay6NHVs6MES5FtIUFr48ePfJNpWg/B++x4rPrKC44HLi2vJIumsWSn2XtCfSPCIhAWxOQIG/r4VXnREAEmhFAOGL9rhe69XkQn4hThOIPcrAZEbGqe3vdbQRh+mh01H2ys2LXLeUsClxY8GZhja6kYg9xSXSU8+fPu7sJEUZatY5HHzfiAxN8wrGQ00aPfZ5uLV8rA3eZNPpK46WbkXLtFaFN2VijaTcnIjVEbTY1EwFELhMUhPp6B+4sH330kbEbp7un5PM+/ohiLOeIZCYUrRy0j4WXWOv5BQELO4KfOOscsKMsvvPrhe/yumePfyMdIh3LOv7j9ImxOnH8uE+ennScWmmv0oiACGxvAhLk23t81DoREIHNJJDxqUYsIviygjeqxn2A82msli5qqQeRRoHpfZQdV68/HgiP193tYpT454TCcxcVduZsMoFAmN6+c8fuP3jgMc/xKUf4IVQRhFhen8RCjrhF6D7mxpG2E+GIsCXaCifl1x+4hXi9T7C7KWVQdohxuG/EnjY2GrtsexDciOEo178hnCsVF8+4pMDnMUGcWuJ9Upa619An+OJPHi478QtBdoKH2GdjJ9xviICDSCeuOz7kWM8Z94H+fnc3oqwncSvK9k33IiACO5uABPnOHj+1XgRE4BkIsCMkVlhEEOdi6maQFXbcs/DOw+6lu2iuEXQb1B+iFhcGNrtBHGfLj+whQBGw3CP+ONlUBp9iBCkhCrHEIvwalUFdfONEeBJ2r+vzz60DK3OhYGfOnHFfZVxANhK4tIs6vJ51XEBIg783PIhx3tACTmjJFgR1cIgr9dKfRv2MNPXXjVyPENAwYGFnTB5aKR92/FqBiwrWcJ9gpL8OsPD05KlTHo+cTX6ILJNtB5v+EPkFH3HGhb8BFp8i1JnsINTxg99/8KD7zWN5b2Vs6vuuZxEQgZ1NQIJ8Z4+fWi8CIvAMBBCRuAuweLFvYMB36qz3gUawIcZJh1vD8uKi+zS3Wi2iMsQ4UUK4dzeZugIQtcShDrGPKAtBjoWcNjCBYHFhZWLCxRxtC6t7XXH+iPi7/N13fs9kg74R4g9B/ryOmviMtjyngmMis551/omryeXcT/s3//RPLoKZgHFsJMhjHBDK+OYzOUKQ856xQtxj+WZs2YmVxZzZMhHe+Irfu3PHfd2J337nzh1f7EpkmkNHjnjscRbI8jfGmOsQARHYfQQkyHffmKvHIiACKYGwSiNQu9Zb8Jhu0uMW54UFt6L3VCotCyesoLibxOmCvM7ijLhD2BHujmgcWLQ5EKUctO31N97wTWnwW37w4IEv5sT66q4s6/g9k5/v+E4j9o8dO+bPiMrnJfxqVvF1rOCIUzYJoi018e69av6PTzbgVMdqvVxe/jr+44wzJ5sMEYUGizSLRnnXaHKUrYOxifwsMGWRaxx84xeWoydO2OT0tN/Ht7jiBsNkijFjQSmxzAl3SEQajoMHDrjVnqgtCHwdIiACu5OA/r9/d467ei0CIoDPOEIt3eHShXCD6BaIyJWlJXdFIKIGAotIHNUWfaJxUcF6iqBHHDdyWcGlAx9vxDaiEb9sBCaxz+/fvet5z549a+dfesk3wcHl4fe//719f+OGL/akXQh92uUW5ToRi/jD3QVhTjtws0BkPo8DPtTZqF4vP0R1XJ9HpfVlpK41LuLrv2X80bFyE2oR6zic+YWk2SQBsZ4tk7+V+oPJHOEl8Qd3wU54xoxbEos28VFHkLOBEoIcn3L+JhDg+I3j8sJC0+c1JvVt1LMIiMD2JyBBvv3HSC0UARHYJAIIIEQR0S1effVV9+vFpQDXjuyBlRv/3/GJCRsdG3PxjGhu5SAk34N791ywIdQQ2vUHEwPiTyO4iVaC9RrXByyrCG8WZv7yV79yl4lTp075Ik/CGBKqD/cHhPaXX3zhG+YQaYX2Zg/cVSqTkx4WEKv6nuFhDxeYTfM09/SFicAk8b8nJjxiSH05THQOHDzozLLW5fp0z/KMUI51APjg1x+0kzFFBBP3mw148AXHBWi9AyE+PTvr4z43P+/CfN++fV4PlvE4GCsmOPSR0IVMfu7du+f++76AN422cuPGDfvt//pfHibx0cOH7ld/+NAhY9Guu6v09Mh3PKDqKgK7kMD6/zXahTDUZREQgd1FAGGFoMKFAbH83XffuSV5za6cqcsFgpwdIgnth083fudZYbYeOSzSbB2PuK4X+uShDCYFWMfZ1h3XBUTlzOys1/XBBx/Y9zdvumgjHWEM2TQH9xPEMJsCXbt61S34165c8X4gQLMWaxfOy8tuoac99IV3LR8ZAZrNQ3/cJWNszIUuDOsPhDIh/cIloxVma8pYp+5sGsbQ1wGk/t1MtOr7zzOTHNxGEMAIaCzmjQ7EOHyYfDHRICIKR093t7ulUF8c3NPH4aEhX7jJhI4oKjDOWt/5VYMJFGXDjbE+evSoR1fxX0W0mDOQ6ioCu5KABPmuHHZ1WgREIEtg7759LpKwgBKCjljSLJ5EPMXBM5vwIIpxMdjI7SOEFwL+m2++caHv27lHgemVhXwIbFwX8G92oZ+GCsQ/mckBCwO//vprbyPCHes4+fAtrx454os0cY1gAefvfvtbt5pj1Y2Y2Ah8rNOURx760IowRmySFpea+oP+IcAR+MTTjvCKWWbkQfTGdvVP4pLRrO76tpAWlw9EP+IWgcxundF/T1+tejjITz7+2NnhZkLb6F/9wUSHBbHsgnr9+nWPJY5rClFasPhTfrYv3PP+hbNnfYLC3wljlmWBCM9OyIiucu6ll1yQ49/fynjUt1PPIiAC7UPg8f8StU/f1BMREAERaInA0OCgi05E8ci+fb7RDgI3K6hwAyFaBn7aP/nJT3wxnocozFhLs5VhYcW3m9jXly5edJHcyILM4sL9+/a51ZYJAUIbcYYARPghGMl35bvvbGlhwd5+5x0Xcfl0YSYClDyIdNr/7cWLLgax0IbjDYIVIY4g7+7pcSHasgBMY7PDgjPycY9oxerMpkX8AgCz2pGGO8S1hz4SVz3y1tI0uSGt+2w3mAzUZ6N/LFRlkuSifHDQLdQugDOTKlxFPl9edmF97vx5Z4HfN/mpjzHjREzTn79+9JF99eWXPjmj7J+/957/MgHHrCCnPbzDnWhudtbFuW8itc6vENSFIGddAPHbG00K6vuoZxEQgfYmIEHe3uOr3omACLRAAAslgu7lCxfcivmnP/7RQ9hhKY0DIY4luJrL2eUrV1xgnjp92sVmI6GJWCUMHufde/dcuCL26g/8xl997TW3uuMSEUKPMhF1LhTT7d1xu/j6q6+8CATl4OCgi0ksvYheRCPWdvrC4sFcauWnTEQn4frcKtxg8Wp9uxDc7DLJhII47LimIBwph4MJys3vv7dr1655OMh68Uu63p4en2zgW713ZORx4ZkRy2vqr1YT3+25udXwjpnJwJq06aJNFmsyKSHOOBMhfOkZv9XfOMzLZPElIpv2vffee8mCysFB58KvCoS2/Oxvf7MrV6/6Lxu4qzDOuDXBl4lSjFG2HXDdt3+/+4SP7NljD+7edbej+jGHIWXgNsMvIoxVo/KyZeteBESg/QlIkLf/GKuHIiKX17EAACAASURBVCACGxBAJOW6u+3Fc+c8UgZh6XA1YaMX3B4QwghO/IkRWN9duuTiEvFL3ohLTTUIWfJgYb349de+KQyb+cTCQNIgssnDeeGVV+xnP/+5+xMj6vhGGdmDOhHHhA9ETGIxRxwSJSQszxG+z8stldaIPNqIS0V3b6+LQe/vBpZnyqO/LBjF9xm/aBZB0kbah6sKvutMOFgsmW2x969YdEv0wcOHvW9YrhGeCHn6g8BHOPsC1Lr+UpaL6ulpF8iUzwJJn1ik7jbUEUfw7B8Y8M172BAJVxPENeUHT+4ZR1x77t+7Z924BLE5z8GD/isDkxgE+J/+z/+xz7/4wiOjwPPkyZO+4BaXlUbWcdoBU8YE9yd+6bjV3+9jXi/IEeP8qkFZCPj4RST6oqsIiMDuJCBBvjvHXb0WARGoI4DYQyAhcP/+H//RF25++MEHHqIu/JERV0RNwQ/5zu3b7tpAdBQswLiCIAwRjyzCvH37tn3y17/apUuX3LUjRCECr7NUsrMvvmivvv66/fgnP7ETJ07UfMejWZQVkhOBSt1Y3RHkhNAjhCJ1v/jiix4mkQkAIhS3GiYTWeswkTzefOstu3DhQhLur4HfdNQbVxfFLGQdG7M///nPLsxff/11j5bCRIUFru//+c/uIoMFPeKFu2guFFxw/v0//IPXi1BmExzcaBD3RCHBtQZLNAteXZRHxemkhgkIoRoZA/KwoRHWZF9QS6z2jo41kw6yY5F/6eWXnQfjAzOEd9ZViHHw8JMrK/b+++/btevXrb+vzwU1Qp5vCPaHDx64WCbqDb+ccCK46V+jg/FisoL7E2PLRIaoPPV9I7wlCzpZC0B/WpkcNapP70RABNqLgAR5e42neiMCIvCUBBBUWC4RST/9u79z0YSgQzAhIBFqWIURd4hJYkkj1Fkc6EJ3cNAF+dTkpH3xxRcuyC9fuuTuHohAX4TZ1WWIU0Tbuz/+sf36n//Zzpw+7WI8XEGi+finI/DwMcbiSrnUffPmTfdHR7AiUnHBwPJN9BAirhBej9B++F8jUPFDP3funFvh/ReAVjcFIrrM8rK72nz00Ucu9hHUuFogNvHH9onJnTsuOmk/kxIswP29ve7m8d4vf+l10wYs01jFEdmffvKJffnll/bVV195Oe7uEh1HkFcqHj6Q+j/68EOf4LD1PNZnJkxwYVzqD9xWTpw86bHGmRDFOgAs/UyUGE8O6iM2OPV/8/XXPlnwyU+6uVEJ157OTvcJJ5oNbkWI6GaRdfj7oU38/ZD2+tWrdunbb+ub6D7uLOZk7PibqB/3xzLohQiIwK4g8Ph/0XZFt9VJERABEXicAKIKC2j4Cv/jb37jFteL33zjG/R8/PHHbp1G0OFSgejCGo01FgGHqMPKiljFaoyAD8spghJrNle2YMcN4vixYy5i662u5EF4Dudy9t4vfuHW1M8/+8z9uRHDxBUnjB6ifHZ62iOo4DPNSb0Iw32pSwRWeCzbhEvETaKRkH2cxOob3GTGHj2y+dlZ+0O57AIfccuJKw4scJ3Bn/38yy97W/G5xj+ayUbsiMlkAmvxnbt3LQQ+E4es9Xq11sT1Bys/EwwWjd67f9/jh2N9ZoISvzhk88ARsT4yMmI//elPPRQhMeYR3sRpp821I3UtioWvWPDpB/lZbIkQf+udd7wfjBfjwbhsdPB3QN+ZPDSKcw6nUydP+qSsftw3KlvfRUAE2peABHn7jq16JgIi8BQEEF1YLjnfeOMNe+mll1wI3rxxw6ZmZlyYuTtI6veMC8utW7dqYg2hiIUX4es+x52dLrpfunDB3nnnHQ+NRzQO39WR6B7ruEBgacYt46233nLXFCzmiFOEIaKbOmgr7iscEXcbMYpFGiHKQsRf/PKXbq3GIkt5rYjKwIaVnX7ga41QJbQhkhR3FvrJLwospKStiOR33n7bTp4+bRdefdUtwdkIJuSjbqzeMVGhrZTV7CDkInURvYR+I+AbifEoA5GLlZpxIxQi7WLRLpMVJjBwW5M/Fdm0DVcixv31N990y/47P/qRC+snsWTDGNYI8r7eXm8zfaZ8WDLZI/54TFSi3bqKgAjsbgIS5Lt7/NV7ERCBBgRCtIZrxJkXXnD/8j179/pCR3ZjJC45LhxEX8G66iciHUEekT/SGNzE4UYYxgY5scV61NOgCf6K74h6BDaiEtcLRDGTACYF9a4eiFEEIaIdsYv4Q5QjnBGDG9W3ph1Y6bu63MqMqMfqG+LYxX+6kJH6WDCKCD565IgLdKzzuI/gjhF1ko5+I3bpDy5ArR6UQRx1hPHp06c9fzPrMumxTjNeXHE1wY0EUc4vG3DzCU0+iWJDWUx4cLmBHYKZnTwR1dTZrK76PsAZsU0IStYG4DbDLyZMWrCOh1hv1eJeX76eRUAE2pOABHl7jqt6JQIi8BwIIMQ4EVEs+MQ/GbcL/Ll9AWAals8FG5bcjPXVfaq7u12cIcgRalFeiNSNmkg6xB1iF2GOD7SL8eXl1QglmUIon3jjiHdEb9RJOa3WGcWRnjCMLGr88U9/6q479Ik+hi82ExZOBDl1IbrJRzvq60MYcyKM+YUgFoFGfRte0z7QBue9YQZzBghqJkMvv/yyRz3BOu+RcyqVWjtpu49X6gNPP550rKI55OMXBcQ39fILBgtgmYwwqUGo86sC3OoZRRm6ioAI7D4CEuS7b8zVYxEQgSckEAKQa4g1rKy4IiBOa24nqXWc4hFbHYjUUqmW5wmr9eSUwxlt4L6rUnGBF8I4yuVbCNYQx/HtSa+UhWXdLbp797rFHeHKES4f9XVFG5vVRR7OH+KgD352dPhkIKzscKMPvgMpbEnHbqapMG+lH03bzyZDLIotl2uTFxbnspjT/dFZb9CCP3rTOvRRBESgrQhIkLfVcKozIiACm0kgBB5WV44Qps3qfN7CC6GdVv54tc9R5NFuXDgQ5Vh36XNYdbP9ft79e7xTz/4mxi0s+pQYfagt03xCdkzIWCS6vLTkv1bgskRUG8aHSRi/pIRbEWKfOOz8OkBUHr7rEAEREIEsAQnyLA3di4AIiMATENhSMfqEAvIJulVLiiXZ/a3rNu7Z0n7XWvdsN8/SB7hMTU0ZkW8INUmseaz+LALGLYVY6Yh1/OSxlONGhOsPkXVwfYpfGp6tB8otAiLQTgQkyNtpNNUXERABEXiOBNYT5M+xih1XFExYHIoQ/8uf/2yExCSmOu5JbCbEItqTp075Dq2ExMQ6zsZMvGex6HC6w+qO67gaLAIisKkEJMg3Fa8KFwEREIGdTyBcPp7FqrzzKSQ9IKoOwvvatWse2/zK5csekhHhzUZJbDTEIlcWjxKnHYs58edZEMymUOH20y481A8REIHnQ0CC/PlwVCkiIAIisO0J+ELUlRX3eWbXTI8AMj5uS4uLNZ/q6AQ+1rhcELub7eeJDEK0F3ykI4JLpN1N17CQEznF+Y2N1RZusqNrHCwM5RwaGPCdPo8fP56EUPyBFrRGO3QVARHYGQQkyHfGOKmVIiACIvDMBFhkSAx1XCnY8RN3i+vXrtkUGw3V+YnzPDE+bt8XCvZFusslrhcs8sT1otk28s/c0G1cADHm4chZzyzbbEI8Env8wMGD9vKFC77zZ21Bbjah7kVABESAfR1EQQREQAREYHcQWJifdzeKq1euuBhnMeLdO3c8tjmW3+wRFnIswV99+aXH0sYPmk1/iI3Oxja7cXEibjsRSaWRC0+49+wdGbGjx4/bufPn3X98aHh4V/LK/k3pXgREYH0CEuTrs9EXERABEWgrAkT+CMv4n/74R7v/4IFbzBtae9M42uRBkOMzfejqVTt06JCdOXvWd7EkskgjUdpW0Oo6Q8xyfMHZ+Ie45r5DayaNC/Zi0U6dPm3/8Otf2yuvvuohD+U7noGkWxEQgccISJA/hkQvREAERKA9CXR1ddme4WGPAoLQ5mz1yBcKNtDfb0P4kvf313a5bDV/u6SDw549ezym+G9+8xu7cOGC++Sz2JMDkY6v/SuvvGLv/OhHHuYQn/tn3myoXQCqHyIgAg0J5KrNnOAaZtFLERABERCBnUiAnUUXl5bcRQUxXq5zU2nWJzbQwSJeLBRseGTE/aN3m3U8+LA4NhbFzszO2tTkpC2vrLDbkEdR2TMy4lZx/O1xb0GM71ZWwUxXERCB5gQkyJvz0VcREAERaCsC2GDwF38aW0zsaomVeLcLTPjh6rO8vOzRaGIDJfzqsZDjoiIh3lb/r6POiMCmEpAg31S8KlwEREAERKBdCSDK6yc4TFRCiO/2SUu7jrv6JQKbQUCCfDOoqkwREAEREAEREAEREAERaJFAvsV0SiYCIiACIiACIiACIiACIrAJBCTINwGqihQBERABERABERABERCBVglIkLdKSulEQAREQAREQAREQAREYBMISJBvAlQVKQIiIAIiIAIiIAIiIAKtEpAgb5WU0omACIiACIiACIiACIjAJhCQIN8EqCpSBERABERABERABERABFolIEHeKimlEwEREAEREAEREAEREIFNICBBvglQVaQIiIAIiIAIiIAIiIAItEpAgrxVUkonAiIgAiIgAiIgAiIgAptAQIJ8E6CqSBEQAREQAREQAREQARFolYAEeauklE4EREAEREAEREAEREAENoGABPkmQFWRIiACIiACIiACIiACItAqAQnyVkkpnQiIgAiIgAiIgAiIgAhsAgEJ8k2AqiJFQAREQAREQAREQAREoFUCEuStklI6ERABERABERABERABEdgEAhLkmwBVRYqACIiACIiACIiACIhAqwQkyFslpXQiIAIiIAIiIAIiIAIisAkEJMg3AaqKFAEREAEREAEREAEREIFWCUiQt0pK6URABERABERABERABERgEwhIkG8CVBUpAiIgAiIgAiIgAiIgAq0SkCBvlZTSiYAIiIAIiIAIiIAIiMAmEJAg3wSoKlIEREAEREAEREAEREAEWiUgQd4qKaUTAREQAREQAREQAREQgU0gIEG+CVBVpAiIgAiIgAiIgAiIgAi0SkCCvFVSSicCIiACIiACIiACIiACm0BAgnwToKpIERABERABERABERABEWiVgAR5q6SUTgREQAREQAREQAREQAQ2gYAE+SZAVZEiIAIiIAIiIAIiIAIi0CoBCfJWSSmdCIiACIiACIiACIiACGwCAQnyTYCqIkVABERABERABERABESgVQIS5K2SUjoREAEREAEREAEREAER2AQCEuSbAFVFioAIiIAIiIAIiIAIiECrBCTIWyWldCIgAiIgAiIgAiIgAiKwCQQkyDcBqooUAREQAREQAREQAREQgVYJSJC3SkrpREAEREAEREAEREAERGATCEiQbwJUFSkCIiACIiACIiACIiACrRKQIG+VlNKJgAiIgAiIgAiIgAiIwCYQkCDfBKgqUgREQAREQAREQAREQARaJVBsNaHSicB6BKrV6nqf1rwnHWcul/P3cV2TqMFDq+kaZNUrERABERABERABEdj2BCTIt/0Qbe8GtirGy+Wyi3GuCOx8Pl87t3cP1ToREAEREAEREAER2FwCEuSby7etS68X49nnrFW7UqnYysqKIcaXl5ddiHd0dFixWHRxHmmz+QEX79saojonAiIgAiIgAiKw6wlIkO/6P4GnA1AvnnnOvgsxzTsEOUIcUb6wsGCFQqGWFkt5HJGfK/mjjPiuqwiIgAiIgAiIgAi0IwEJ8nYc1R+4TwjoOKPqrLgOQY4Yn52ddct4iG6s5IjySB/5dRUBERABERABERCB3UJAgny3jPQm9TOEdPYalm3ecSLIl5aW3Do+PT1tpVLJrd+I8c7Ozscs4ZF/k5qsYkVABERABERABERgWxGQIN9Ww7GzG5MV5dl7fMcXFxfdOj45OVkT5PiRI8g5wnWFqwT5zv47UOtFQAREQAREQASejIAE+ZPxUuomBBDSWMNDUIeFPAT53NycTUxMuAgP63hPT88aMU7xkb9JVfokAiIgAiIgAiIgAm1DQIK8bYZyazoS4rn+Gq0JlxX8x2dmZmxsbMwt5CzsxDre19fnizzDQh75orx41lUEREAEREAEREAE2pWABHm7juwW9ivEdNZCPj8/b/iPj46OGq4qCPCuri4bHBz0Z95xkDfyb2EXVLUIiIAIiIAIiIAI/GAEJMh/MNTtXVGI6LhGbxHl4bKCKMeHHOs4Ahwxzrvu7u41UVbIkz3qy8x+070IiIAIiIAIiIAI7HQCEuQ7fQS3QfuzAhrxHJZxmoYYJ/44izrDSk4aIq1gMcevHLcVfM856svaBt1TE0RABERABERABERgUwlIkG8q3vYvPCu+63uLyEaQsylQCHLikPMeQT41NeWCnJCIzcqpL1fPIiACIiACIiACItBOBCTI22k0t6Av9UI63EtCjCO2EeMs6sRCzonFPCzkCHTShIV8C7qgKkVABERABERABERgSwlIkG8p/p1deYhxrnGEIOdd1ncc1xTEOOIcizkRVzh5z7soI/JHebqKgAiIgAiIgAiIQLsTkCBv9xHepP6FgObKWS+ksXhjCUeEYwVHfHNFfGMRJ8pKvOcd4j3KrC9rk7qgYkVABERABERABERgWxCQIN8Ww9B+jUBcZwV5WMixjiPIEd3hwhIuKyHI24+GeiQCIiACIiACIiAC6xOQIF+fjb60QCBrzeaeE2EdFnKEeNY9BUHOyYEgD6GOKMdKTj7CImbLbaEZSiICIiACIiACIiACO5aABPmOHbrt0/AQz3GlZSHIQ3SHvzhiHMs5B64qfA83lljsuX16ppaIgAiIgAiIgAiIwOYTyG9+FaqhHQkgvhud9LWRhZyY44hyLOFhJc9GXuE+rOTtyEt9EgEREAEREAEREIH1CMhCvh4ZvW+JAIszObL+39xH/HEs4OGyEiEOYwEnAhyXlfXcVlpqgBKJgAiIgAiIgAiIwA4nIEG+wwdwq5of7in1Qpz24K6C6A7BHdFUIspK+Iln3VkQ7QMDA9bb2+sxykPob2b/og+bWYfKFgEREAEREAEREIGNCEiQb0RI31sigDCPEzGOP3i9IMcSzruwoOOmEmIdlxYEOu4sCHbSSDC3hF6JREAEREAEREAEdjgBCfIdPoBb2XxEM0dcuQ8hjsUbkT05OeknwjsEN+mIpMJiTtJMTEzY6OioDQ4O2vDwsFvXi8Wn/9NsJOSjjY2+eSf0jwiIgAiIgAiIgAhsEQEt6twi8Du92hC42Sv3WMcR2gjyqakpP8P6jXU8rN9ceSZdCHLEO6I9fMxbZUS92bM+X7Sx/r2eRUAEREAEREAERGA7EJAg3w6jsEPbEEI3e8XlBNeUsbExe/TokY2Pj7sVHJHNgYUa/3CupMVyjhDHQh5pcWXB0h7iPcR2I0zZuuN7pI8r7+M+0kdaXUVABERABERABERgqwlIkG/1COzQ+kPYxpVucB9+4whsBDnWb6zgCPKsGCc9ohuLOJZ0BDxpsaZjYUesb2Qpj7rjWo+S93HWf9OzCIiACIiACIiACGwXAk/vqLtdeqB2bCmBEMNcsWiHu8rDhw+NM9xQ+J6NnEJaBHcIeEQ5aRHlWM27urrczzzy1Pt+1z8HBN5n2xTvua6XJ5tG9yIgAiIgAiIgAiLwQxOQhfyHJt6G9YUYR2DjboKVOyzk4T+OAEcQs5gzhDHvEORYyUmHIOfEok4561nII3+g5DnOeEebol0h0OObriIgAiIgAiIgAiKwnQhIkG+n0djBbUFc44KCdRtrN/7g4a6CuA5RHJZxxDbpcU3heywCJR/3sbizEZIQ282+RZqot1FavRMBERABERABERCB7UBAgnw7jMIObwOiN4Q1lm6EeAhyxDbfOLBiZ4VyiPNwW8E6jmU9rOTkI3299ZuysuUEvnhHuXEf36J+ytIhAiIgAiIgAiIgAtuJgHzIt9No7KC2hLgOUU1kFSzbCPGwcofbCWmJK57NE6I5rqTFss5CUBZ4EpOcd+zcmXVzoYzI0wxXCHLS1x+N3tWn0bMIiIAIiIAIiIAI/FAEJMh/KNJtWg/CF9cTBDnWccQ4Fm6s3nxDiLMws7Oz06+84+CKsObkO8+4qUR+xHlY10PMxwLPQEkeznifFdrZe9LzHGfk11UEREAEREAEREAEtgMBCfLtMAo7uA34guNaUm8dx6qNdRshjmjmmSviHQGdtXqHPznvw1IebisDAwMu6gMRojqEePaaFeBxz/f6I/su0tWn0bMIiIAIiIAIiIAI/JAEJMh/SNptWBcCF0GNdRtRzqJOrOPd3d1WKpVceNNtLOEId9IhxvnW0dHhJ+8R4iGwoyys7txHCEQENKI90mXFdRZtCG2upInnbBrdi4AIiIAIiIAIiMB2ISBBvl1GYge2IyuMEdWcvMMqfvDgQbdsI8w5EOqcDx48cFHd09NjWL85yYOIR5QjwHFRQeQT05x3fEOII6xDXIfYpuz697wLIZ79Fu+8QfpHBERABERABERABLYJAQnybTIQO7UZiNw46QOW7/7+fuvr63MrOYIb63gs1sQVhQOhPjw8XBPuCPCIRR4LOXkXQh9rOvU0O0Ksh/CO52Z59E0EREAEREAEREAEtpqABPlWj8AOrT8rwhG+uJUgxA8dOuR+4ohtrOCIayzcHIjrcDnBCs63kZERz4eQx0UFwR4uLZTJUS/EQ2jH1RNl/on39fkySXQrAiIgAiIgAiIgAtuGgAT5thmKndWQrCBHZCPGueKugiAeGhpykc4zrioIbU7SYPkmDd+woO/bt8/DHEa0FgQ85SPYEeoRqSWEdv0VcqSP9zxn7yXMd9bfllorAiIgAiIgAruNgAT5bhvx59xfhC8WbQQ5Fm0ENs9YxyNcIS4ruJwgxjlCzJOXNLivEHec74hy/Ma5Ug7fycs96bNCO7oSgjuuUU+jtJFHVxEQAREQAREQARHYLgQkyLfLSOzAdiB4Eb+IZgQ4whtRzLuwlIewDnEcojm6y3sEN2IeazhHCHLSxncEOeXyXF9GlBXp43vUGddIp6sIiIAIiIAIiIAIbCcCEuTbaTR2UFtCGCOUOcIqHaIYkc6Be0r9EYKZ9yGWyR9WcMQ54p6TI2shry9LzyIgAiIgAiIgAiKw0wlIkO/0EdzC9iOmOUOUR1N4h8AOQc37EOH118jDNfIhwEkX+dezjJNehwiIgAiIgAiIgAjsdAIS5Dt9BLew/SGgQ2RHU0IoxzXe16fjPe+yJ3k4eVefP9LH+7hG+fXXRvVtlKe+DD2LgAiIgAiIgAiIwGYTkCDfbMJtWn4IW66cWfEb77BwR7oQ3YGj/n02P2miDO7r88b3KKvRlfz1ZTZKp3ciIAIiIAIiIAIisNUEJMi3egR2eP0hrOu7kRXU2TTZ9/V5Wn2O8uLaaj6lEwEREAEREAEREIHtSECCfDuOyg5rE5boZuJ4I0t1M5FeX248x7UZqlbSNMuvbyIgAiIgAiIgAiLwQxCQIP8hKLdxHRuJ7fjONe4DB4K5/oxvXENQR5rsN92LgAiIgAiIgAiIQLsQkCBvl5HcRv0IIU2TsveNmrjR98jTarpIr6sIiIAIiIAIiIAI7BQCydaJO6W1aue2JxDCmWvcR6Prn+P9RtenzbdRufouAiIgAiIgAiIgAtuBgCzk22EUdnAbnlQsP2n6HYxGTRcBERABERABERCBlgjIQt4SJiUSAREQAREQAREQAREQgc0hIEG+OVxVqgiIgAiIgAiIgAiIgAi0RECCvCVMSiQCIiACIiACIiACIiACm0NAgnxzuKpUERABERABERABERABEWiJgAR5S5iUSAREQAREQAREQAREQAQ2h4AE+eZwVakiIAIiIAIiIAIiIAIi0BIBCfKWMCmRCIiACIiACIiACIiACGwOAQnyzeGqUkVABERABERABERABESgJQLaGKglTKuJqtWqPywtLVm5XLbFxUW/Vspl82+5nOXzeevv77eOjg6/ZzMcvpF+YWHB83d2dlqhUPDvq6XrTgREQAREQAREQAREYLcRkCB/whGvVCq2srJid27ftomJCbt586ZNTk7a3Oysv6e47p4ee+8Xv7CDBw9ab2+vi26E+/T0tF29csUo4/iJEzY4OGg9PT0S5U84BkouAiIgAiIgAiIgAu1EQIK8xdFERGPhRoRPT03ZxYsX7f79+3bx66/t0cOHNjk1ZcvLy14aQvv0mTNuJe/q6nLr+NzcnD18+NC++OILW1xYsPn5eTt27JgdOHDAurq73ZqubeVbHAwlEwEREAEREAEREIE2IiBB3uJgIqBnZ2bsj3/8o3178aLdvHHDpqanbfTRIxfX4bqSM3Nr+eTEhCHCh4eHrbyy4qL95vXr9unHH9vDR49cmL/26qv29o9+5MJ83/79LspbbI6SiYAIiIAIiIAIiIAItAkBCfIWBhLL+Pj4uN2/e9c++Pd/tw8//NDGHj2ypeVlq1YqbgF3z/LUvxxLN2J8aXHR8C2vVKvuOz4zPW1jY2N26+ZN++arr2xqctKKxaK7sPT09lpfX5/7lctS3sKgKIkIiIAIiIAIiIAItAkBCfINBhJXFVxRvv7qK/vqyy/t8uXLNjE2Zgup2G6UnQWcOU4+5nJW6uiwQ4cO+fN7771n+/fvtz//6U924/p1++1vf2tzCwvuS37k6FEbGhpykd6oXL0TAREQAREQAREQARFoPwIS5BuMKWJ8dnbWvrt0yf764Yd259Ytd1HB8r3ukcu5EMfSjSgn2srI3r3W2dVli0tLNjg05Is7v//+e/vi88+tt6/Pjh49aqVSya3kWM11iIAIiIAIiIAIiIAI7A4CUn5Nxhnr+NjoqD24f999xhHQRErh/UaHu51khXkuZ93d3Xby1CkX3kRp+etf/+qWd+4//OADF+4HDx0yQiLKbWUjwvouAiIgAiIgAiIgAu1BQIK8Heai9AAAIABJREFUyTjiejI1NeWC/NGjR+5HzuJNDmKNE0ccv28s2ljRsaavNLGcYynfu3evu7D8+Cc/8cgsV65c8QWfX3z2mSHG33rrLQ+VSFqJ8iaDo08iIAIiIAIiIAIi0CYEtFPnBgPJgs7llRW3iidbAiV+4YhwLN4nTp2ys+fOuUsKz4j0jQ5cU/ApHxkZsWKh4As+Wew5PjbmkVvYPKgVK/xG9ei7CIiACIiACIiACIjA9icgC3mTMcJCPr+wYDMzM8bOnFisiRs+MDho+/bu9Tjjp86c8Y2AENe4tly6dGnDjX7cst7f74I+l8+7ZZ06ONlgiOgsbBikQwREQAREQAREQAREoP0JSJA3GWMEOZsAsaEPccgL+by9/Mor9vLLL9urr71me/bssb7+fl+4ee7cObt965a7uODe0vRgsWc+7wKfRZ8RyQV3GKzjuL5Qtw4REAEREAEREAEREIH2JyBB3mSMEcUIZOKHu4U8n7fjx4/ba6+/bm+8+aZv+oMvOW4tLMTEZQWf8tHR0SalmqenTEQ+Ypx6OClnJXWPaVqAPoqACIiACIiACIiACLQNAfmQrzOUIZIRyFisEc64rLDz5pEjR9ylJLvosqNUclGOQN/oQNzfu3fPfcYR4TpEQAREQAREQAREQAR2LwFZyNcZe8Q2J9FOiB8eizUR6LiWrCDSS6VkZ00zv7JAM0Q61zxhDzlSCzh5Z2Zn7f79+77J0M2bN93yHk0gdeSPd7qKgAiIgAiIgAiIgAi0NwEJ8ibji6DGBQWreFdXl7uVEDP84jff+Pu9+/ZZN+/xAy+XE/eTtDx/l7qhYGHnZNHmjRs3jFCHv//d7+za1asu7smCEMevHOHfipW9SbP1SQREQAREQAREQAREYAcRkCBvMliIZPzCBwYGrLNUcsF98eJFm56Zsdu3b/uiTtxXunp6bH521kYfPfJFoFjQiSu+MD9vp8+ccUs5Qn5sfNzu3rlj9+7etW8vXvQFoFSPCI8wij29vS27vjRpuj6JgAiIgAiIgAiIgAjsEAIS5M0GCpeVUslFOYIZKzhW7Vu3btlnn37qfuSvvPqq7RkZsWq57CELJyYmXIh/8P77dv3aNXvp5ZddyH/yySe+2JOQhljL2UgoDsrGLYZQh30I8q4uua4EHF1FQAREQAREQAREoM0JSJA3GWAs5AhkXFYQyZbL2fzcnEdHmTJz//I8u3US+rBadaE9PT3tkVIiVCILOFm4ef36dZudmWkYzhALeVdnp1vGS52dbi2XL3mTgdEnERABERABERABEWgjAhLkTQbTBXl/vw2PjBiuJB3Foi3m827xJhuLNIk9jihnQSaRWRDgRGRhQ6Gl5WV3byHtwuJiQzHON3dX6elxf3QWkcYC0iZN0ycREAEREAEREAEREIE2ISBB3mQgEeS4kbAB0OnTp+3h/ft2+fJlGx8fd6s3Ahx/8UYH32LDn0bfs+/2Hzjgsc1fePFFr49FnbKQZwnpXgREQAREQAREQATal4AE+QZjy6JOBPL58+c91CG+35xsGITofpaDcrGuHzt2zH7+85+7v3lvb6+irDwLVOUVAREQAREQAREQgR1GQIJ8gwFDNJdKJcN63dvfb7Nzc9bV3W2Xvv3Wo6Q8iyg/fPiwnXnhBfvxT37iYvzAwYPuFrNBk/RZBERABERABERABESgjQhIkLcwmPh0E94Q15XxsTEPgcjiTezjRE3BNQV/cq6NDtxP4sRfnPKwjCPGf/WrXxmRWg432P2zUVl6JwIiIAIiIAIiIAIi0F4EJMhbHE8WW2ItP3f+vEdd6R8Y8B03b33/vU2Mj9u1a9fcYt5IlCPA2WCov7/fDh896vmxjp998UV3hTlw4IBHWJHfeIuDoWQiIAIiIAIiIAIi0EYEJMhbHEzEMtbtEydOuLUc95KxsTH78vPPPdIKUVVIQ4hDP3LEXUmOzs5OG9m71/bv22cXXnnFfcZffe01279/v4dMpFzEvg4REAEREAEREAEREIHdR0CC/AnHHOGMgB4cGHB/7+Kbb9qZs2ft5MmTNjU9XYu+krV2F4pF6yWsYXe3DQ4O2tDwsBFZBYs5lvds2idsjpKLgAiIgAiIgAiIgAjscAIS5C0OYIQxJMIKoQ4X5uasWqm4tbzY0WGvvfqq+5Szm6cv9MxYyHnmxN989NEjt4aTF2u6+5MrzGGLo6BkIiACIiACIiACItB+BCTIWxhTxDRCfGZmxj7493+3q1eu+G6dWMvxBR8ZGbE33nrL9u3bV3M9yVq9CZF47+5du3vnjn344Ye+2+fBw4ftxdSHHH90IrnIbaWFwVASERABERABERABEWgzAhLkGwwoYhxL9oP79+3O7dv22//5P+2jjz5yUY27yclTp+zo0aN28NAhGxoctO6enlpElSiaMlj4efPmTfvwgw/swYMHNjA4aD96911Pi1/6vv37tbAzgOkqAiIgAiIgAiIgAruIgAT5BoNNOMOF+Xn77G9/s799+qnHH0dcLy8ve+jCG9ev+yZBiGxCI3aUSm7tzhaLcGcBJ1b248ePW3llxe7cvWsfffCBjY2O2o9//GP72XvvuaWdBaBZ63q2HN2LgAiIgAiIgAiIgAi0HwEJ8g3GdGlpyV1VLn7zjQvoe/fu1SKp4C8+PjHhwnxyYsLTsWizWrdQE0FOlBUs7a+88oov5BwdHfXoLJSHD/qJkyd9keiekRFfNLpBs/RZBERABERABERABESgTQhIkDcZSGKKswHQw4cPfTEmYQ5Z0IkLShyxONMXei4s1MR6fOeKxbuUhj7ETWX/wYNuVf/24kW7feeOYWXHtxxr/Ou9vdbb2ysreRag7kVABERABERABESgjQlIkG8wuLMzM747JyEN5+bnbWV52aOpkC2Xz1tXZ6cLaEIbItNXpfpqwQhyQiX29ffb2XPnbHB42O7fu+di//bt24aV/LPPPvNwiC+eO+fhEYm+okMEREAEREAEREAERKD9CWg3miZjjCUcX3GipGC95jkruDuKRTt16pRdePllX9i5d2TkMf/xbPE1Yd7XZwhvfM4R6jNTU3br5k27f/euzUxPe52NdvzMlqV7ERABERABERABERCB9iAgC3mTcUSAEzt8fm7OBTlJe3p6PBpKZ1eX9fb1uU/4iVOn7MjhwzY0NNTSRj8s3Dx85Ij7lSPIp6am3C0Gl5iZNM45fuc6REAEREAEREAEREAE2p+ABHmTMUaQT05N2YOHD21ubs4XbxI7nF05z730krEA8/ChQ777Jn7hRFhpJUIKaRDcuLlYLudiH9GPewwW8sWFBXeDadI0fRIBERABERABERABEWgTAhLkGwwkoQrHx8ddJLNxD64mhCl8+5133ML9NBv64I4yhyV8YcF3+yT6CucCO4AuLLjLCpMBHSIgAiIgAiIgAiIgAu1PQD7kTcYYUUzMcBZyIqKxbLMbJ5sBsbEPVu5WLOL1VRBKkYWc42NjDaOy1KfXswiIgAiIgAiIgAiIQPsSkIV8nbENCzVuKPiLu3tJteoW7OmZGbduI8ixkLciyrGAszB0ZmbGI6x8+cUXduPmTUOc6xABERABERABERABEdi9BCTI1xl7RDZnf3+/ET2lu7vbKtWqXb1yxbp7eqy3p8ejpAwODTWNrELxWNeJ1kJMc/Jf+e47+/3vfmfXrl3zuObrNEGvRUAEREAEREAEREAEdgEBCfImg5zP5ayrq8vjh2MNZxOgmzdv2kq57PHHDx8+bHv37fPIK0RcKaULNfE1Jy1C3DcMWly0sdFRmxgft6tXr9qNGzfs8uXL/kz1pOckf2ep5KEQW7G6N2m6PomACIiACIiACIiACOwQAhLkzQYqlzM26PGIKIWCC+x7d+/axMSE3btzxyOhEF0Ff/KTJ054tBWEOaEMXYwvLNjo6KiL8UvffWcTaVhDIrYQUSUO3GEIhcgOnf0DA9bV3d2SG0zk11UEREAEREAEREAERGDnEpAg32Dsenp7DbcUXFYQ2kRdwQ/80cOHLtb33LplfX199uDePRsYGPDY5L5rZ2odxzLO4s0rV654vvBNz1aL4EeMs5Mn9bXql54tY2vvsxFhclvbFNUuAiIgAiIgAiIgAjuMgAR5kwHDbYTNfliMScxx/MnxBccNBWGNFZxNfbB44x/ulvRisWbdrpTLvmiThZvz8/Oep1F1XZ2dtmfPHrewd3d1PXX0lkZlb/67rBivr63Btwav6nPpWQREQAREQAREQAR2EwEJ8iajjV83Ipzr2bNn3ef7qy+/tPv377tIR5QjzjmxnD/tsW//fnvjzTftzAsvuIUcN5ln9iGvCd/azQbNW8eyvc7rDQozs6g3rplXG2eu5W4h6VMn8a5lmvd4QQ0+bshjwwSPV6M3IiACIiACIiACu5qABPkGw4/7CMeZs2fdOj766JH7kJcrFV+4uUH2pp99MWehYIcOH/aNhhDkLCL94cV402Y+w8cQtHGlqMx95jZbyTqvs0mez33Tipp+fD71qxQREAEREAEREAERMDMJ8g3+DBDHuKIcP37cOjs6fIEmCzC/uXjRJicm3G1lgyLW/XzgwAE7efKkvfnWW3b2xRdt//79Xte6GZ7pQyowH9OZDSy6DV6tX3XOJXZrWag8czbMlG1gwwTrN6XBlycuLZuB8rwJ9S8bVJQkbPRB70RABERABERABESgKQEJ8qZ4ko9Ysg8dOmTDw8O+MHNgaMjGxsdXt7lPQxw2WrCZLR5xn0/dUQipiBj/1d//vb3y2mt29OhRXxxKXc//SAVlK7ryCStvVmS1wcdqCPIcH+OMSuP52YU4JTaoPipqfG2YoeHLxvn1VgREQAREQAREQASegoAEeYvQsIoTZQW3kr6BAd+p8/atW3bn7l2bmpw07om+0kiUI8QL+bxvKHTk6FGP2nLw4EG7cOGCvfHGG3boyBGPZY7v+PM7UiFZrycbqeRspbmceZIWNHFSdM6VbzVNH9mSaqopD1JWrCbGa1K54u/5lpxJimjOatPjLkqPFBtf1+suJVFqrcSogiIbZfKE2UQb1V0reaOE+i4CIiACIiACIrDLCUiQP8EfAIIZf282AxoaHPQY459//rnd+v57F+hsGERklfojl8+7u8vI3r32+uuv28lTp+x1hDhW9z17PMwhZSPmn9l/3CtPhWO9fqwJTT6EYIz75Fqfpb4v8VxLV7uJL3FFjHOfEeU5BDcvq5Y4uvCEUC+nJ8KcSQlpNnaFWa/qWs/SBLSDd/WThmhpbX7gzV2v1Oz77H3UVitNNyIgAiIgAiIgAiLwRAQkyJ8Il/kGPljLjx475sKcjYDYgfP0mTM2OTlp5ZWVx4Q1gpxdOInYghjfOzLi+TtKJSuXyx46cXFhwTcEIg2W+OfmupIV4dn7Wr9XBWUI1viUlZ3xbvW6ms/fMZlY/ZjcVRMxXq1WEiYIcRLlq35Wc4jxSvo/RHkizi0Xojy1mDdoSP0rnuvr9xZVE4O3f08T1adL2l/feJ6jFgpJv9dcberTNyy1PpGeRUAEREAEREAEROAxAhLkjyFp7UVPT49vFsRmQMQjf+utt1xcYyWvVio1Szc6DnEdu30WCwX3I8ciTqhE4piPj4/75kFY0InqQnos5c9sLc8KcO5rz/QxVafcJl4nazoe+nPNyyYPj8tRSgg1zD3W70SQuyjnm1vMU1FerVilWra84UPPmavZyOvbstFzNNO7WzWrpBmSUuuUe31hkbmmwLMJuM8+1xLrRgREQAREQAREQASemoAE+VOiC8EclmyENC4niPNGBwK8XmAvzM/bwwcP7NKlS/bN11/b+fPnfYMgLPCkfz5HxrpLgSHKXRVnxWVjSb1eGyJ1Iq4TnervskX6/dqJAKK4yuLWfM7yZHCLc8UMK3r6P+4TezepHz+yVcTX5F3Sqlrb0o/xHGmlqWskdCMCIiACIiACIrANCEiQP+EgILgR3riaNFrAGe9CfMcz6euPiYkJu337tn391Vf2lz//2cXyO+++67uD4rYSZdTna/15rRiuifENCkDcZkVv9p6sjwncdd55NWlm8iDe/cT6nf4C4O+9vnBvSSznSQuyNa3ex5zisW6sJnnsU7R7gyQN8+mlCIiACIiACIiACGwmAQnyJ6CLuMbFZH5uzh4+fGjz8/O1HTufoBhPSlnXr12zb775xq5evWqzMzPm7i7rqs0nrSFRwIkeTq3kNXN2piy3UK8ueORLLLmMVFlBjqCtf669yH5wPxjcTpL/5as548ylZ97f46DCXfL0uFiOAhP3ldWnpGVZVORNu5L4qUfjcYBJC/Y0mffcNvB8T2cc9a1holD/jhLWvlv7VFeZHkVABERABERABESgAQEJ8gZQGr1aXl72nTofPHhg7NZ55fJl37FzaWkpcVPJqsNGBdS9Q5DfuHHDvr140X3JEePuO16X7lkeXcCiEOuUbK2pfEsVZCzojDxcIxvXEJpxrbUrm6j2MnODAA/B7cZvRHnerJqK8Bz+8okoT3zHw00laspK5qgsGp3UEymJy5LI/0yDM7d82+gIDpEucjz+Pr7ENXLoKgIiIAIiIAIiIAJPRkCCvAVeKysrdvnyZbtz+7Z99eWXdvfOHUOYLywsPLWFnGpZzPlodNRdX1j0+TwPl64Zi64LylTPhrhM0qwKb/RqSN5IQ5viXfbeZWj6IYfCR2xnOuDS2MV4WMXzlqvkrFomKSstzZ8R5/6/XMHyfqZ+LZlao9ywgEeLam1MvVySdEknvOu1/lNm0rgoixe1fmX67e89UfI1kfhJXn+TzVTrb0bqe97VWmpJdCMCIiACIiACIiAC6xCQIF8HTLzGMo5rCn7ef/v0Uz/ZBAjLOFbumj6LDE9wxR8d3/LOUslDHT5B1qZJ17Yp5/G34132yn2I2sQOnYjhSNOoEr5l9Kq5GOddfaZUmNas45WcWSWfBlvhHhWMZbxgOStaPlfMuK/UakmnA0nhIXOjqpreTl9EG/zKx9TYjgWeulZnDVFS0hmyR5nBI9v35Fsmj39Mnuvf1pR/tgDdi4AIiIAIiIAIiEATAhLkTeAguCcnJuzRo0ceBQVBziJMduRcL5pKk+LW/RRicN0ET/oho1RDbCbXRD4m0UwSEep1ZyzE9VOMesGZbWv9t1ozw1qeXt1vPJxJEOWYxxHk7sqCIE9cVlavSYjE1RamIRPTClbt0eHeUqt5VVkjsVN1nfSJxjze4lp/sgxIlubN2NFrtWdqa3AbJT5eV4PEeiUCIiACIiACIiACJkHe5I8A0T0xOWn37t2zmzdv+jk3O9swukqTYrbsE9IwThqBxlzzXPv+uOzMNjqkZVyz3x67Dz2KS0qtMnLGibWaXIR1LJhhvba8VdP444nYpj28QYjHmdjwk7xpGbUGJcLchXftXdq58FUhY0aQexNChMc1ZfRYn+JXgUYf9E4EREAEREAEREAEnpGABHkTgGEhv3/vnkdBiV04m2TZpp8SwR36OHulwclzVsmG44XLVu9TfOXq99kXkWzNNVKmCdl9M1e0XD61iBc6jB05q7mCVXK5muxO3E6SFlWtbKtf0kgx3mC+U25cecw2KB2GKv2O9+m7x57T+UH6uT41r2vv0tWwtedsntrL2k1UqKsIiIAIiIAIiIAINCUgQd4ED4J8enrao6rgR16phSdJMhFLu9jRYYV8/ol216Rcjojc0qQJz/QpkbUhuFeFJyI1acHqt2xFiaSMFKtfQt7yfdVtZPV7TR9nNKm3IZdawBHlhfRPjmu+mNjBc4kt3CO1V80KXjUWbczsrAJNreQ1B28SUAmWcXzF0wrdTzzM3dHHpLVsRpSR1rVGP97L5FNaYi1dxHBPSl3NtcrhsRyreXUnAiIgAiIgAiIgAk0ISJA3gYNwnpubs8nJSVtcXFzd5TLNw26aIyMj1tvXZ/29vUaklFY28/HFnJWKC/27d+82acGzflpfJPIlZGWSKp6SOiNnOIP4W0+yanNOrNmrkrS+tSRPxH8+sYTnEeQlf1stdFilULRyvuB28BVf2hklJLlYMJoI4LIvHk3mMdGyiMaSPqeXpHU8JJFV4tmb7mnWpl81f6d1u997wiLpH++T55i++ELWtJhoMdfkVYMP2US6FwEREAEREAEREIE6AhLkdUDiETHOSRQULNmIaGRZ7DA5ODjoQvzkqVM2PDxse4aGrNTZ2ZIgp9zllRW7cf26l4/1nbJD9kUbntc1JCJX70OmrvhWXxfvkzNpVSKOQ3TiHx7vMyVkbvmanIldvZLPWzVfsIoLcLNyrmgrVrBly6cn8VbSI4f/eOJVTileF/UlVSbO6TUXlaSha4V3ajmv9TNrLU+9W1yvZxocdaeVhBivt4iHpbyWPJpcaxyNbFRufQ49i4AIiIAIiIAIiEBCQIJ8nb8EhDcb9fT39dmekRHr7upysY1VvKuz03723nt26vRpO3XqlA0MDFh3d7fxrRULOYIcgc9OnUePHrXL331nV65csUq5XJN16zSr9ddu6V2bHJnIiQMIR8jG0Lnp69r7REqTLpG7NUXsGRLXEL+NArIiGTFMEiIcmtWs4EuWs+Vq1RYqZvN+Vm2+UrWFatXyaZuTaCtMgHBlIT45FVBKKqzdHz3tTY53eVfZSSsTMR4tpk9J86K3Sb8TwR0NT3q+miJ99klHlBRp4xq04prNTZrsc6TRVQREQAREQAREQAQeJyBB/jiT2pt8LmcDg4O2f/9+6+npcV/x3u5u27Nnj/3dz35mr7/xhh06dMi6urpcvNcytnhz+PBh46SMoeFhO3nypAt737GzTty2WGSSLNWMSEKEZwjwxP1kTRJ/yErMREbyJnmLpTr7rlZGZEot5cmiSl4mcc8pmE9EN1zJmy1bzhDji2a2UKlacaVsU8srNrm0Yn3LZeteLlu1WLFKPpH/RbeXVz1KOS3IuT95tAQXGO4TIZ5EacHknRXj4Uue9CSV8g1lcljDaXP2npxRo5fiH6PjobmTFAlV/SsCIiACIiACIiACT05AgrwZs1zOenp7bWhoyDo7O90CPrJvnx07ftxPhHRvb6+/b1bMet/wP8fNBcGPuEfoc7bqi75eubX3qXZcIxmryVLIjKxcY5VfOw9YFaSPC9ooIa5JrS6UU6t4IsZztpIzW87nbClntlg1my9XLL+yYlNLyza+sGw9C8vWtZQI8jKuLUWzki/YLFjF8lbASs60gsZ5ZxLR7uLfX8RzTBfW9DiZXNSs72tt10lK3GJq1GIukryofcgkIFPajkwu3YqACIiACIiACIjAUxGQIG+CDfeT/v5+27tvn1uw+wcGrLOrywV4qaPDOLFmP+1RKBbd/WV4zx4X/ljhS6XSM5XZqC2uH3HBTjUlzxl5uebedWa2kNQq7GVk33PvhVSSq0dSSUzMFYIVpptxJteclXOceVvO5W2Rhqys2OTiko3NzVvn7LwVpudSsd5hy6WidRXy1pPPW0fOrCOPpRx3oKQBySUR4Uk/sONzsMB0dZFpkr7qwVrW9jgtp+bWk6GRuU1S1b2oAWpEJD7GNSlB/4qACIiACIiACIhAMwIS5E3oIMhZsIlv+OEjR+zAgQPGAsxHDx96XPKl5eWWF3I2qobILWw8xG6gU1NTtnfvXuvGNaZFX/RGZTZ8h6ZEfKZX0mQlo0vOzIvMbajux4v1TKsLLWOHz6gi/MbLObNyPmeVYt4qxYKVC3lbQpyXyza5sGgPZ2bNJqZsqaNkU0sr1t/dafM9XdZX6rABF+YF6yoiys19zIlwmLQvbPZ0LRHn7rBCFMToXzoDSVJ6g2v9gMVqP9NWp0mi/FriNTeRK6585D4aln2/JqMeREAEREAEREAERKAhAQnyhliSlwhy/MO5Hj12zBdwfnfpkk2Mj9uVq1etp6/Pjh075m4ruJngc97ykcu5CCfs4d3bt+3e3bt2+oUXbN/+/TUrOfU+zbEmVyjk7LWu0DXp676teay5b9Tbm9MSfIFl8q1SZUufqrm1nF8RikWrFlHWRVtZzNsKMd6XlqxzZtbKnZM2Zzkbn5u3vu4umx3ot/6uThvp7bG+zpL1lgpWKuSsVDQr5nNWcO2LX3nSOtfRxIRPF4byHH1KxHjiRc+7RLqvfl/tSSj0JMdqv6Ok5E2CgAZk36f3tTjppI0pympJG9097XhvVK6+i4AIiIAIiIAIbG8CEuQbjA8iqVgs2vHjx21hbs7u3Lljd+7etQ/ef98ePnhgP/vZz9x6jmsL6VoVVbl83kZHR+361av27bff2qVvv7XF5WU7f/68C3xcV575qBfhrlzXN3o3rQ8lGvmzCUOYplekr1vHq0RWIcpKunFPsWD5jqLlSyWrFhdtxczmlpdtfHbWFnI5m1hY9MkPEWwmh/fYYG+vzQ6bDfZUbbCnZN0deetBmBfNOgs5n/wgzMMqjiSu766L7zSWeRK2sZrR0Yl//OOyOQQ5Ja66v6xmzIrv9B4efrv63AhVYCPKjmcJdvFBVxEQAREQAREQgV1JQIK8ybAjnMbGxnxjoAcPHtj4xITNzc7a/NycuaV8YsKKhYIdPHTIfc0R5KvCbf2CkW0I8tu3btmVy5ft+o0bdvPGDTt95owtLS0lMc8Rks8q2EIfZtVh3MeVZpKO50i/ftNrX2pJ05tscehNnrkmAh1rdt5yuOIUC1bN5w1XlsVy2QoLi7ZoOcsvLlmh2OHn7ELVBnqXbHYpbwN9ZRvp77bezg4b7Omw7lLB+kp5KxXMOovm1vJS3tKYLEnzaFK4pHDNuwBGgFfS9966dH6RbXliP4+lrDUoufBMT747qGw2Z1gjUmPU6Ia/qRDk2e+MdaP3SdGtlZ0tT/ciIAIiIAIiIAI7h4AEeZOxws8ZwUyc8Pfff9+uXrliuJggmh8+fOguJwh23FqeyDpOnbmc+6PPzsz4xkMrZd84vklrnuOnejGilYVGAAAgAElEQVT5zEUnluQkFGFaWLqItCbOmVy4Uk7EJU0gFjsbJC0tLFp5adkquSSqysxSwbq7lm1sIW99vcu2d3DZ+ns6baSv2wa6S7a3r2g9HXnr78pZJ7sJFXK++LOYVpHEM082FsIyniz5JJJK2O/DoX51EkJ7El/0xAPdRbl7seRrdvKk5avhFL1DoZXrmcZ7n5isfswKcu4R4iHGn3kC9szjqAJEQAREQAREQAS2goAEeRPqCCYWXs5MT9vdO3d8Ix+eOebm5vwcHx9vUkJrn4jcwsZCm3YgDlc1YWuW8IygXOuOkS2IFqcJ3YqcfU4+eWrEOTudVhLrMMKzkMtboZC3YiFvlUIixMuVJEb57PSi2VzO7i8QhWbJ9kwuWV93p+3v77Whni47PFiy/q6C7esrWF9nzoY6i9ZdyFuuIxG3uLJ4S3zHz1oL0xva4M40ycZFNTt5WMeTyZJVE2FOUZw8+R2aPg5mG2ldaYL40vAaYpwrR70Aj/f1mevT1X/XswiIgAiIgAiIwM4mIEHeZPxYpEmc8aE9e2qLO5sk396fQjg2amV8q7+SNt41ytfgHckji9+jPSv4rlRdlBsxyKvmQryzWPQdUK1YspV80ebKZuXlqk0u59ydZaI8b7n5so0vVqyn1GlTM8s21NNpC3NdNthVtKXhDhvsKli1r9OWSgUrEI6lmLdCMZ9YndNFpvwagaWcloU7iotjX3QaXuRsaISJPRHi3rXwUc/006U0/+B6wnv/Z1Vch5dRiOt6Me31tijI6/NmmqFbERABERABERCBNiIgQd5sMHM56yiVXIwTinAnHalOXNvkUMv1H+N9NnWo6uw7v48PaSGIS/4Ple1WX1xEclawqi/qxH/bXUXKK2bLK2YrZeOPrlQsWn93tw2wGLaz26rFDpstm00vVS0/Zza7nLO5ctGWyzmbnluyhfmyleeXbLpUsOVpLORFW5jttMHuDlsY6rGBrg5b6k/eL3Ylccy7CjkrFgiZmPdFoOGMYlZ0KV6plj0STCKtEwi0HeGOz7v3J32uphFUXGiHO05NjSchGdMMfol/ssIcgR2nl50+R9r6K3klyuup6FkEREAEREAE2o+ABPkGY8qiTTYAKuQTq+sGybfF53q9XWtUaOlVw27yKdGgtWTc1JLWbtZ8rlmGawIVKzhHupu9u3Zb4r+dr1R8IyA2A8qXy0b8GJgOdnfbXjZb6u2zfGenza2YTS1WrdhZtun5qo3PV212yWxpecUWyitWnp232VzVlqbz1lvK2+Jsjw12l2xxfsmGejttcanbhns7bLGv5BFZektF6yzmrbvEbp95jOdsL+SLO6vVShKSsVox7hMres4X2+ZTK3mylHPVh5we+ukLM+nsqstKaoAnrEzCAVt8mMvTN46nbiOpSBPC3Utdx4KeKUa3IiACIiACIiACbURAgrzJYCKW2KhnYHDwmTYAalLFpn/K6MOMyq7p6aT+VEMiNkND+j1f40VYgz0HCxtTy3iIU18wiY9H4hSCmMVonq9Uk3Ol7GK8WC5bJ65AxQ4b7u62AwN91gff3h5bqORsZtGsb7Jsk/MV659atqn5sk3NzdniwpKtrCxZpbxiM+WKLRVylqss2zSW8ZVl6+8u2eR8tw31dtjIQKf1dXXYcG+X9XR2uJtLZ0feuop5K+G/7jb8pNOJIE5ENy5KfM3xvZrayr3/6WpRYovnqv5rgGvmFJKXVOMEID6sPUJwhwDna/Y+Uke6eNZVBERABERABESg/QlIkDcZYwQTPuSDQ0PGwktCFeZTSzlXt6o2yb/RJ8RXBbeEOqvpRvla/V6ThRnB7e/SZ8qppUkLDQFPkvjG/WqW5M6/0X73DUeEw8Msh6U870++zhGXFSzkOXzHV8pWQJBbzvoKBRvu6vKFmoPD/dY70G/LVrDZZbO+ropNzpatv2PBJmeXbTRXtRkzmy4v2WK5YuXlZVtYrti4rdjsQsEWlpesu7NoY/Ml6+8t2chMl/X3dNmBoT4b6Om0+apZb1ey82d3Me+7fhatYkVvddUK6eJPJDi29FzVJXm200HH4ykiyoEDg+DCuxDYyHpn+xSW7ihDwjxFrosIiIAIiIAI7AICEuQbDDI7cHanUVB6enpsaGjI/Z6PHD1qfX19LtR9q/sNymn0eXRszHfonJyctJkZJOdzPlK16OI5l6ytjBpCbMfV34e6rAnNRFqSJvGoTnInb8NqHCWm31D0aaFYyAvVqp/FStWKlYoVyxUXrl1Wtd4CEVI6bG9vlw0N9lgl32GLlZwNlCo2M1+xke6STc8u28PuvE3PdtroVMFm5ks2szDv4RJXbMUWyys2Ords+YWcjS7krXuqaINT3dbX02UP5xZtsKfbHs0tebjE4Z5OG+gsWV9Hwbo7CtZTKHjYROKYd7g/N01PILgHDoLaH5k00b/EOu5XX9RJahLAIuk0z8m7tVziKSu0s/d8DzEeaeuf472uIiACIiACIiAC7UVAgnyD8URss2smohxr+cGDB+3woUP2zrvv2oEDB6x/YMAQ7U8jnohx/v+z9ybckhzXeeCXe61v7QUgFoIkQBJcRFCyLZ+R5DOSxse/2Me2PEfH42VkigDBIUiCIkg2VgLo7rfVmnvO+W7EzcyqV++97kaLIoAosF5sN25EfFHN+vLWjRtv/exneOedd3Dv3r2ee8gNk3qMZtJEy49tmD/Tua2zurSsnLxLmTOthnraFqm2pJzuGqqgoSuJCU9CEfqSh4yqYom5X1dyYDKqawy9BpPQw34S4GgYw49ilI2PcdBgNa5xkARYrgocDX3M1gkejENcLAd4MI+wynPM1kukZY51UaBgKMO0kegtZ6sco2GKWVphOkpxtsrEUn5rMsTxaIjD4QB7gxj7Ax/jKMA48tEEQCzL4CFUa+knSdbDqiTnlpQLIZcrj7hoe/iTFvL2QcZAxs/ENunub12/bfvzw/J2Xb+vyzsEHAIOAYeAQ8Ah8MVBwBHya/aShIhkO04SjMZj7O3t4dlnn8VLX/ua3Kp595lnJH74k0Zg4Y2fvAH0/oMHMg4PjqpLzGciY5Yz95fW8mVLr/tllWOd6drZeM2lOiSWKmVScUqhl0ptrcdiTGY/Iyg3ZILuIIw5bi7uiRpayEuJvuKVGfwyR1AWiIWcM2Khh9rzEA49ObQ5CoB0HGI6CrDMEhxOI1ysRji4iDFPMzycB1imGc5WK6RFiTUvF6obrNOS50dRlR4u5hkWixTjJMHJZIRb0xxHk0L8yw/HJfaHIfYG5qIhXjaUBGa+jGVOFxY+UOiDhQmdyPXZt4DCwOTExyAnEVsUf2Ky4VtO13uDj6aKar+83UdlXOoQcAg4BBwCDgGHwBcTAUfIb9hXku0kScSP/Pbdu6CrygsvvojnnnsOt27fxpOScQ7Lw6KT6VRIfRSGEslFCfkN03qk5h51FHlDBQ2d7N9vw0ZtU8Usk1dqfS2OGPb2SwpZoun71jqugpLSymwPdZKQ+56EOmSwwaCuJKqJV+bgO6hKRHWFuKHbCOBJmEIPZQ2MIoY9BCZDH1kZY39CIp5jOg4xX2cYDz3MVinicxLzHGdIkRYVirJCyhtA8xSBn2M+zzGI1zgbFTjfr3C0V+NoWuIoLXE0jnA4ijAdhhJKcZKESAIe/mRwRCCUQ6AGIQl8qetTUi6A0aGclnI+jqjTi7JyRbRL++SbeSXg/Xwn7XIOAYeAQ8Ah4BBwCHzREXCE/IYdJuEeDAb4sz/7M7GO3759G0dHR0KmwzBsydQNanY2Z2mK05MTLJdL+EEgVnLq/Cwk//JAhinzr8kZiT7Z7vdRGbV1G/tvy79FlDKGbhqXFdHF8IEU1kbr3kGKKiEQPT08WcGTQ54F/KqEx3fNy4IaiQ5Ofs936DcSprAKeIlQgKLyJYTh3jDAKPawzAfYGwWYr3Psj8YSq/zB+RKLdYbZMkVe1sh44LTk7Z818rJCVqVY1x4usgonyzWm8xiH4xgHE6a0wCe4NR2ApHwS+kh8D0MY6z4t4PzHEtAlR/6j/bxDi1kh2ozCIiR7d5hMJd99zJnv14uerbpteVd2CDgEHAIOAYeAQ+CLg4Aj5DfsJS3WtJB//0/+BN/5zneEOLNOSbOSpxvUbDSzT13XmM/ncqhzdn5u3CLCUPSTnPUJ2kbnxyooYTQEWkm4po+iSu29enmOalTeLYZyIaMk47yNkxZfsknj7EJyzbIvkUwaId4+Kvg1yXgFkJxbQm6IOyTqCbk93UbqoEEQeKgaD0nkYVr6GCc+0rKSy4CWWYlpMsJsWWASDnA+X+OBt8AyyzHPSuRVjbQCihrI6hLreo3zrMBwFWK4CLFHQr5IcLw3xK18iHXT4GAU43AQim955QdCzPkLAUMmxhKJhbFYFBmDojyMSNYg5MkhTwJx+fV09vayXlfjEHAIOAQcAg4Bh8DnEwFHyB9x33iwE3EsRJqEOs8yCVnI7o9FsNg3z3F+cYHf3bsnBzofPnyIsiiQ5TmKokBVVa0v+SNO77IYrbQbtZtlGrBJHZVgG1F7SLPXc1PHpry4Q/OPfcvDiY1LLlFJWuWks40h5V6NgG+/gS9WcFrOjVWcFJ6WckP+G0SAHJ1kfHC6aLNckhR7IfI6wMD3sS5qDIIIy0mJ/STE+WKIg8kAszTH6bIACftFWiAta6xrurI0WNU5ZmWBMPMwzkKcriKcpWucrodY5plcMnR7FGMviXA0iDGOQuzFEYYBD5x6CD1ILHXrtSNoteuVWOZE0yC3/cC2/Vnpl7dltdyX2dhSV3AIOAQcAg4Bh4BD4AuBgCPkj7iNtGjzvVqthFCnqxXKxyTOJFh8p+s1PvroI/z2nXfw7rvvik5a4enCQrJOQv6Z3GHswUEuzdJCId7b5Jpl5cxduuGI0VJzumn0X1yH1AgZt+4acuulSvJEI7XS1t29PXM/piHjARD4SsbVim/8XkjO+R8fHHgolJpC30fte4h9H1XtIfED5BUwCiOsJ7SYh5ithphOB7hYl5jMcsxWBaLZGvMsR51myIsc67JEWdVo8gbz3MNsHWCWpThfp1gLIY+xmIywP0iwno4kVGIx8jCJQ/CaUbqy0Nedccxl/kSCONgHCxJoRaGP2Xa+T7SVfG/LuLJDwCHgEHAIOAQcAl98BBwhf4Q9Jlk6Oz0F44X/+Mc/lhCF6+XSXOqjZtJH0CMiTYOyLDGbzfD+++9jMZ8L0WeEFVrHsyyTVCzyj6rzCrmWMNt20loSW32zmnmTGut4v431fRrOvL5NL9tfK8U3xbYwT+O5HYMX1TeMr+LVEimQFmXeh2TeJLMVwHbx0Ta9ukcDc2CSGsyDgCfW9sZaq4NRgHHtY5B42M8jjPcSzLMae/MCF6sCk/MVZqsM4/kKp+s1Zlkm4RKzskRdVVgz8kuRgw9ZxWqNs0GI+WSMvUGC8/0J9gcD3CYxHzJmOi3mvpB/RmRhZJaIh1bt5UJctsBhPxdKtPtpn4grjqxTGa1juku23+7yDgGHgEPAIeAQcAh8/hFwhPyGPaRVnET5ww8/xHv37uG//Kf/hJ+++SbSNL2h5/XNJF+Vtbrz0CJJOq3jtJJzvF3k7HqNO1o3LOXGtYRGa6G7ZI1KyG2gFFJJtrX1Ns/Eil9KtUKIo0RcUQ1Gi6HWJNK1ecuNljZUImN8+yTojE1ewbOEnNZmnYmOSxZPq3mflHPskFFZQh8MfZ4MPEzqCMNpg2XeYDStMKOlfBLjYpVhch5juohwvkwxX68xtxZxhkvMixL5ukbFQ6FhiOUox3iQ4GKeYzoc4GQvw3SU4NmDEaaDSA5/juMQB/AwCICRDe0o87WWcoFPYO8w4b7yrURb0x7Ubfa6tlbIZRwCDgGHgEPAIeAQ+Nwj4Aj5DVtIizUPX9Iy/sY//iN+88474mJCAv20XiTmDa+DT9PWJeazEHIlsUoDhdxa1xJxrehNXAy5jfHRZpvpo3S4x8T7fZjXQazPdENTt3ht2FGpuGYV/6tRexUqj3byiiXUkpecpdk16qaC1zB6CV/UY3Jt2R4Mpc+5zNAMIeSWhLwmZQ+AIS3vAcm+j9HAxzABllmEg2mE43mCs8UaZ/MYZ/MQsyVvAW2Q5UBRlGC8xaIqMavWWK8LrNYFkijCw4s1RoMEJ4t9uWTo2eMKe6MId4tILOaHYYiB72Eaeog5QTqtSGJmb3AnEmZV3F8JRKP4sd5a1XtQt0hs110u6253LXbkruLaXG/Pr5V7nMZuTjvn0jU/mtKdSh6tq5F6TAWPO7/+VB5zqH5Xl3cIOAQcAg6BLx8CjpBfs+ckTev1Gufn53j7l7/EP/7jPwo5p9X8ab6auhZruVrJq6dI9oXYbpFxQ9Ctb0WfdLCK5dZifvMqW19pEhCrsk0tGScNJQ0XQq5EvJGalowbqmpxtXNST2zhNrQ08yIikvL2Vkx6pJvLMinDmOHsmrDK98RPfZR4GCce0jKS8IYH4xhniwSnwwgnSYDz2MdZ4GGxCuWSIcYxr6oaeVYiy0qs1iU838fZIkcSJ5jlwHQ8wKKqsT+OkGYJ9gcBijjChOb6QYAhLfaRL/HX6WOu3Ey87vnQoxXtPZ8G56sIeX8X+tul9ddT6V092LM3Cf2lRBVupX0Nm702BSnXtfd79eVs/c7mrne/x79Ifuf8/kVm4gZ1CDgEHAIOgS8BAo6QX7PJJOT0G7//6afi650XvAny6ZLx/vCkI/QlfxRi1u93VV7oDYnFVeRC6smiycAtGWJCS/cNpFyJ+CXVVl07qDB89V0nGTWhEY3l3FjPtZXr4PCqW/IyL3OdvbEy0/JsQytaK7pc2EM3EeIHc8GQxDMPPSQNOXKAovYxigKMQ19CGh4PA9yZhDjfY6jEEc7nGc4XKc7mK6yzXC4aYuxyWs3p3V5WwCqrwDCIF+scWZFjMgix2ichj7AYD7Afh0j3TBzzvWGIJAyQhObmT48HQe0Cia3JGyrN/RZr+VUbaV2PWqw3LOltre3dL1v/pKv0tvUym7bU18DK7XIryIztepWMabatPReqDR1tZ2Y257Ihd1Wh16VVdUmWQte3XuqiFVd3e/T59uaoal3qEHAIOAQcAg4BRcARckViR0rL9WKxwOnpqbiTsPzP8YqiCDzEOR6N5BKiMIqeDikXImHZX58MWcJ9eS1kDZ29dReF2cUrOIzWtw8TJOK20nB9Q8GJIN8tIbc+1TIXygvZNE8DvO2TL6GyOkA7lnEJ0S4ktH1CTmJOgzWt0nXDN6Ox8O1hbxDgYOBjOQ4xmwxwsTfC2SzD6SzFx9EFZssVzjwPq7TAIufBzxplwcgsDc7nS7GkZ+kaozhAukgk3GJ6MMHBIJYLifaGMdZlgmFSyyVDdGGJQh5ENbeWysMCMSARt29iwpCP/ddmqd+ieSOhcrpzJt0m4yqlvFSQM2j2sKVUT9LkqcrK9ER1Ehsp+6pm02C1ydr6mtmqc+xpFblHGWxbF1fd09POSmfUVjxeZnuYx+vtpB0CDgGHgEPAIfBICDhCfg1M/C4u8lzCFD5Nn/HtIQ+PjvDCCy/g6y+/jNt372IymUgc8m25xy4rP1FSsWFZtdpUpqd8R1Wv1RAuUal8iq22UzuU9GClIUoknx1VsxZ5CgvTYxt/GbBvVbadSrDvTT2mp5keP8zaKqotudRhYh+IIg8jP8AkiJElIQ4GiYQ4PJ7kON9LMR2EuFgO8fB8gMUqlwOgyzzHOi+R84BvvkKRA/M0QBr4KFcxLuII6brEdJjgIqVvOW/8LDEdRaCLzCjxMRnEYi0fRMbHnLHM5SIkO0c+THCenL+8tsg569qHHStrJW0f9jZod5Ta1JmyzXPPJNvZ5Nsxew9j+ugpD0+U57v99UNHNmnXvzf/DRE9pGvnwLY+QVe2r6vvk3LK9gfY0CuKegI9/VbO1Fyu76u5Vn1fcEPNFb2uqO6rcXmHgEPAIeAQcAhsI+AI+TYivTJdVnit/fnZmUQ/YdPxrVuYTqfY29uTq+5ZR7L+yccfizWdBzN5k+dLX/sappOJudHTEmHq45sHRU8ePhR/dMY1v33rFn7wgx/gm9/6Fo6PjzEcDp8OIW+ZTM8kTrLTJ+YtUe4tvJe9ll+QoJGkbAmZovlrrJbM05maJJB5hvgjJ7NWTTqHk5AjgMcA31Zh11cnpIzQ6NC/nILSS6bUYNxgNqioicTiexLLvAp9lAmQDxpkJbAcF1hOBzgaRVisJ3h4vsJ8leNktsB8leJ0tsQyyyR8IsMllgVQwMM5bwQNIixSIIkzfLyoMR7EuCVRWWLc3h9gynCJew0mSYCDUYhJ5GMYehIuMfItMbcuN7IOIaRcc58Beq0FvbUEEwCDpqRyN+pGX2Xf1GN1WdzR1Ibgt3vSSogkf1FgD01lAHNOVrKbf4xuTocWf32ZnI5tUxHdzts+G8ScE7C/7qhC6cuCjmH1yJhto0hvllSB9tPyDWlfieRtRb++nUtvWlSrMo855A0zcs0OAYeAQ8Ah8AVFwBHyazaW5Jnxwh88fCiHO0m0X3nlFbz8yiv49quv4uDgQCx9dGv5L//5P+N3v/0t7t+/L+4n/+E//Ad84+WXMRwM4AX0nTBknH7opycn+Id/+Ae88+tf48MPPsD+wQG+/o1v4NlnnwUvCOpbQq+Z3qM3tSSJLGGbIZiy/L3Bb/zygMo6uhbVI6SfEUR6b7WCk60IqSThkrjjdEoxVLohKSdhF+5t5qYEtJ1pO4gZV71jjKuGcYkxY3S8iJLUQ4uvvBkykf7mgYeBDwyDENPIxzj2kBZD3JqOxGWFlvLZYoVPhz4uFgFO/BqrjFFbKmQVkNYN8qbC/UUGBDU+yTwM4hwHixyTYYS7iwwHowTPrEvsDyM8sx/jcBhiOgjEp30Q+ojtJUOcjz5YtITOXo4k89d9bEl3t5uERB5CZEt4MyrLEubG2r3tXgnmJs8HIlWpmtgiD0uaNhZPy43Vcm6QN6yd4+q8pb8Qc2q0JRnOMnytEwXSIDPt1ms0b/xVMfMB6DXZBsXDLkbFjSBL2nGzpafIDN9rlgdNFWjrdQ1sUJ0qZFOVvaJ5S9oVHQIOAYeAQ8AhIAg4Qn7FB0Gt2XJZT5qaWzmDAC9+9at47bXX8L3vfx8Hh4fSez6b4b3335eLghbLpdQ99/zz+Na3voWj42NEcdwS8qIs8fDhQ7GSM+Y4D4zSqn52diYWdt7S+dReLSloM4ZHKGmQgXptLG8Vr5qLkl+jqqeQpKjVYTLmAYN5dVXppwyXSOs435Shndf0k1SypqzT1ZLysD4ZNLSbkmoj71ZAMklZzpaUldS/9kx8lzAwN4BGQYyiajCOIqRFKQR9OYkxjYHZMpaDm4s0x9kyx7KocZYDq8pDVnvIqgZVWsAvaizKCsN1jmWWy4VCiyzFwSjCKktwe5rgcJxgOogxTUIMowAD+pnTWk74GvN4QiRoceZ8uWZdt6yA1upuaW1OMDF/ZKWXe6uWTmNv9ww4dgekvr+dFjv2VPIv/044ty05w/TtPrcr2BipnfPlTF9O59uX6rf367fzfbkuz5zRav5Ki22Wmk7U4kG9fTK+PY4rOwQcAg4Bh4BD4LMh4Aj5FfiplZpW8SAIxIWE+bvPPCMW8tt37sgBTHbnNfevvvoqeMEPLd4Mk0irOd1d7ty9Ky4ooq9phLRT/s/+1b/CgwcP8NbPfobff/QR/ud//+9iWf/a174mejmmzuGKKV5TrSSmzywobuu1+ZIGQ4kvVe+oUM2MeNJjLRvuMELSxGppB5ROzCtRI6XUt6k31nHSSNvHJjr3ttitpje+mZUhoTpDM3nqY73OltPmyCZ+ObWbtTeBL7duhgNPDm0OQiCfxNgfmrCIR9MJ5uscn56vMUtLRIsMs6xGmXtoKg+LBiiaCmVWY1UAeb7GxZJhFSPxT58thjg7GMvNn4eTIQ4nA6mnOwvDJfLWT5Jyut3EzFsXnP6dS4KBfRqRvIIiizO/xJAoGxx6QOleaEoJWswFa4uXUS5byjH52kTS1nF8+6sPx2LMd5GzcdW3O9np9iZj9Oz6q8vpRt6aSCew1X3XTCnS1Ztci4x+yjo9nWhXt6miq6fshim9a9LPa7/G5R0CDgGHgEPAIXAVAo6QX4UMv2t5+2IUIRkMjC94T5akmpFRKMM3LeckJvv7+7g4P8e79+6Jr7kQ9+FwwxWFoRPH43FbR7eYe/fuCTEniacLC8n/ExPylrC0md7Mn3Z2N4MxZFzH4jx0Lpo3qaHBm3WGSm6ZXLX7NRzIaOF89G3GF3LfMUJpFuuyHUKvIhJpD6h87jvdWzyQkFfDCKMkREaL+WCAZVpgOFpJ+MPwIsV5WgKrGvOihp9XyHi5UFGAYRNnZYU0a7BOfYwYFpEXTaUFzpcFjqYFjtYF9kck/BH2hzHowkKLOSOzjDwgsmEcScxJkGWNdOzuIcoLT6Wsyxa3FFNnGgx4jfjqG5RMaz+v8kaJ7SFjmpbuFwfmOCYlfd7AavdE/i3YRymzr+xpNKl2k7JOem2QZZVhy67XLk0bctpxQ1DHMiP259OJdbkNfVJQpVstV1SL1HXqttS4okPAIeAQcAg4BIiAI+TXfA5IMAZJIuSZxJyE++GDB3jvvffE8j2wRJ3W7Nu3b8vhThJykuk3f/ITsZKTqFOOBJ5vvvI8x0cffSQHO3kglG+6rfCAJwk5D31yvD/+1y5WonWkvGQmHTvpSJpdGUVVvJXd7COSnYoNSC5Xq1W4VWrk7Tgkksawaw62MqoLyTj5Kwkv50JRMSBb9huHAZomQBz5KOsGcRQjzSvEowHmaY5kmuE8LTBY5JhlFcbzNeZphtmykn3mXq8LEnQPq8xHVhaYZSUeLHIczFIcXAxxMBngaJLgzv4Y00GEI0ZmiQMJizjgxOxCFRnOr/+7gjxcyMK4CP31wea5LLGCs1/q61IAACAASURBVEndgYxC84xCeUO2aTc2v3hQlIc+iYeGrzTe42INt78sCMo6N85J8BQE4YmF3sDPOYmsLMTk2kXZFrPGTkp7bnSRSjtgK9D7DF1q2q7oyrtyVLk9u26YrkdX1+9ha+XDo/lNSVdyCDgEHAIOAYfAVQg4Qn4VMkLMPAyGQwlDSD9wkhGScVrMWX7m7l2JusKoKDyMeXh4KET9448/xqf378vtm2+88YZcLvTiiy+KDIn3w5MT/PTNN/H++++LJZV+4yThtJ7yZlCSOCU+10zvX7hJqct107hMYi6R8g2RjcKG4qtbOrFORnM6R5saNt6xLksayVfZgxw80Et6WCFvobvwAw8VuakfYFjW8GMf0zxBOExwmFcYLlKxfI8GwMUKeBjycqEKi5WHvODFQjXKGmJVX5bAybrEeJljMl/jcDzE0WSEeVbjYJxglVfgxULZwMc48iQqy8D3MBR3GjNH8r6W9CoZ1wcKM3EDjEDREeL214c+JCLJg5mGkBtpCtCHnUSceR4QlUcaKfJhVVT0CKg8gskh3W5PzNMNyzIRSe3QO0L0mBadbatF3UL0waJtuCmjI5mxdQbbvSh1Vdu2bFvWObUVNqNzNB+b7VZXdgg4BBwCDgGHwE4EHCHfCYupJOkYjkbiQpLEMeqqwj+9/ba4ltBX/O7du/jhn/4pvvKVr+CFF18UFxYS78V8LpcJffLJJ/jP//E/4tmvfAU/eO01sZTzECcPdf7q7bclIgsJOl1YaCVXUl4WxeeAkCuFUdLTB1Lb+nVPnn9a2owd2M5XXKBNXshtn4hbiy79yykhlmQSzYZRWXz4ZO5+gtEwQjyKxQI+mcRYZgX2hyTkAT4dNpivI5wtQyyzEvO0QlY0WGU15lmBIi0RrjIkYYj9YYbDcYZFWsphz9n+QA6A3mKIxMTH8TDCJApxOIwwICmPzBFYzo7YmPmBkQzlRcs/X1wX47/rDhlPl45uU0bbSO4Fn54yz6vhNTxkTMWGkHe9hX6j8U1KSiv7JIRc62Qa8sci3Y6n46qE2WPzZKT7dBXn1T67U4MJ27qcSl7+JG3Pg4sw69A+NtWulzqYkS5RepXTflvqXNEh4BBwCDgEHAJ9BBwh76OxlSchZ7zxW7duycFMWq1PTk5wenaG2cWFtD24f18I91/8xV+ItZyhC0mwf/7zn4tLCkMbfvz730sUlTiKcHJ6KoSdBzrpZ6wvWsnlXZbSX+v/+NNtxrFdvmYFV4heUX1Z0SVBrbBsSEmR9CQ9U3Kq7ZpaOiUWckNmDbc1N3yKFP801oIufNwDqWqc1Ch4JmAYSlSWo6GHRTrAswcDLNICD5YZZusCD2eMYV7gwUWKi3WJKitRFHxXKAv6mFfIswoPBiFOzyLsJSFujUPsDULcnY7Ev/zZg7Hc/HkwDMTXnJFZTFQWa2yuzbkHWvn5H58byMrt1IVwM88aRUpB5Wfd1PFnAFrGKUkvepJy+ol3pNz0MZqM9j4B7zR3eLMHJdnHEmURMzNhVluMbiOvta1GZehGuBPVnNWpxc1Uteg6jXatpWw/3xVs7aUxtULTzdFcySHgEHAIOAQcAo+DgCPkN6DFw5cMb0hLuUY+aepa4pPT35vhCnkIk5cAvfzyy5KnrzjdWPhimMPZfC4WcZIeWsJJvJn2X0KI7AHRfv0XKr/BeP6QK6MrhnFJocO4XEgk7h2GTNGybDwNLFkTK6nJc8rkgeIVQnHjfi5WcuPi4iMJPIS+hzL2MQ6BtBjgeG+MVVHheJnjfJVhOlzhbJEh9BaIgwyxnyOjbzn9YJoaWZ7j7KLCculhOfMxDDycjWPxKZ8d5uLWUlYN9ocJ8pKHTAOxmseBicxCX/iAwU6ojtZ+se6bNdhpd6RXrcAk3j0+KWsVYqqk1fwq0FJVgqTKzHOLfRJgpTXPm9g1ai+3m7yLjFOV+UD0ptDK7/6oXJZ8vE+Rrutyr93jXZZriXp/Ko/ceYc+V+UQcAg4BBwCDgF3qPP6zwBJ8mg0kguAeL09Y4qTTNPNhIRa3UzqpsHFbIbVeo3nXnhBDoGOJxPxM6cbispeNRoJPA9xjkcjIfb0W+/feHhVv89l/b8geeHQ5JG19XtmWWmkTIskqzc/5ZzEWc9WCnEnuVfwrVuIxDT3AyRegiKuMa0bpGWNUVLgeDTANIxxPs6wF8V4OMlwtsywWBdy+VCWV8jLGnVZIC9qzFJgTYKfFZjFEdK8xukwwzor5dbPO/tDTOTw5wDDmJcMRSAxH/D2T4nMwuuVzIltLoefY31x3mLV9iwdtlZnkdPlC/E2KzSahOUbnxgJddgDzpjhW9yMbo7G3w+sVmuxVwKuc9FZtdzWPBVps0mlUSW0x6aIlrRVpbW+nVxro2eLSlupraJ9ermsQmt0EPZr+7YZI7VV1K4udQg4BBwCDgGHwDYCzkK+jUivTCLDCCmMnHLnzh25SXO1XMqhSxJzfdGVhW4q/I6eTCYSZYWuLiTzQsZrpX3aYzNl+MTpdIqD/X2xsNO67olv7qacK92EAHdAmdIVstZX3EiqBdjI9nsql2JKPkvXELE69xvYzZZDG4c79n0h+UXTIK8bDKMQ60GMvTDEnHHHhwM8nGc4XeQ4n6e4WKwxX2aYrzLMqxJZTat5haIBqrLBIqvER30YZbhYFxgnER7MaHGPcfeoxmSU4M6eJxbzfRhSnjBUon3wkHnbNdANxRwE5edRD3CatavtWPi5rIl/DH03/uO8wIlRakzfFmYBTU3uxt1lA015GKAujqD6VDedWGSwS9smaqnOKPsMfz+7hp2Dq9r2YUcrrPRWcacOV+kQcAg4BBwCDgGLgCPkN3wU6KbCCCqvvPIKsvVaQhkybnifkDPMIQk1o6zQMk6LN+VJ3t9++23wJs/roqYc37qFb77yCr72jW+IHo1vfsPUXPO1CPTpdV+Q1l5TFopoXTt2SltLOLkVz0lSZkOODVtW3cB6W4ceb/70EIfA2Pcx8nwcDirsJTGORznOpwVOJ2uczSKczVOcLyKcRCFWWSGW8IIWc4bIrBqcrwvMGLElrxFHAc7WJSbDCGd5g71RgllWSPnOJAAvGBonIZLQx4jEnDHVfWMt5z92hjU0wQ9Jhe1qLCSyHPUwb9dFP3ISaSXbJNE9JOQQqAVGeLm29Uk6ibWxuLe/LcghUjuiTIP5bYBN1bV/bbddMtpkV7lL5OY6VaKSqqxf38+rnEsdAg4Bh4BDwCHwGAg4Qn4DWCTbdCchwaZLyW9++1t8+OGHQrD53UwrOgn70dGRHP6kzzlv7PzOd76DqizBEIjpeo2SFnUhIWZA9qNbCi3hjMLCmztf+eY3xcKuvuo3TM01X4mAsqZNAfNQpEcLDUHkPpBPGXraMSvlo0xFm21ifqd2W0kxvTQnpPsILeZ+I6S8TCLsDxocDRPM0gJnwwinwwgnowQnwwTDKBI3FlrCGfqQFxClVYVVWcsD4CyvEPg+LrISwzjCLG8wHSaY5zn2xnRtibA3CnE4HsglRAXMRUN8GCCtluArdp6GYhsmrqsmBrVduMYu9z0+YoiB2xJ4S8iViMtjQ4/cqxOQHsBU5ZbEs8hHAkXR0/E4xk5g+3toN0N1atoX+UPn/xjm8IdesxvPIeAQcAg4BJ46Ao6QPwKkJOW3bt8W95W/+Zu/wfPPP49PP/1UXFd4cRBdWl79znck/OFwMBCSzTLJOYn4+++9J/HLaTGv6loI+9RGb7lz9y6+893v4rXXXsNXnntOYpyTJLrX00LAsjwbzs8ktPYyJIk1exu+aQa00DNhT1JNcku179JqbUTUyUMFzTh2GOlLa3RL9H3jr554Poaeh2noYxr5OBhGQqCPpzn2JyMs1iVO6F+eljihO0uaY74ukBb2BlCeV1jnWOQk6yTmIWYpD3+GuDhIsD+OcWtvZC4Ymg7EWn4wjDEMeQjUR0KrvecjUt9xfeAgN29sVBmSZIuDEHn74CmYSFxyrtm6vcjtn4qU3TMFr8VKubYiZ+V0a3pbbat6NZyKnUz7EMBmW7ch2VfYtbdHSrsqu2n9zhuN3Q8f2xPaFNs5i92V/bFc3iHgEHAIOAQcApsIOEK+icfOEgkyyTXJ9l/+1V/h+9//Pt597z1xSSGxpt+4RlhR6/ZXX3pJorOEUSRk/PUf/UhCJtKnnC4pd595Bl//+tfx8iuvSAzz5194QQg/+7vX00Kgz6YYXYWkU+Npc4yOXtNR3BA/Uu+OdamhV2ekxFzLbbsORZXysn4gWrTcn+4jcchLfkIMIx+TJBIr98G4xGQ8wiKtsL9IMVvnGJzHuFimiBeZWMtJzHPe6lrkSKsaeZkhDHgDaIhhHGC5HmBvFONssRZXljvZCHvDGOnEHAItBjEmUYBR6KOhK4sXWPcVgDHKiQ8t5LoUQ4U98aHXXxI61xO28oHDLFh+7eFa24dJq6VTtoGriG7R4g1RxU3TjcZuf7R5M72pfVP6qZb+BYd+qutwyhwCDgGHgEPgD4qAI+SPCDcJScBLXPb3JQRiMhy2FnLe2jmZTtuwiFRJP3KGQiTpVncWWsh5+JNuKjwsSp0Md8foLOqTTrcK1rvXU0TAwmkSxVYJs7Fi62hKR1VKCXjLs0nWbVeVISln3pBzrVWNHTFljqSXxD/weUjUl3CJvGwoiQJEcWguGRqFYgGfjCNcrIbYu1hjvspx/3yJJS3mqxJFVaOuajRVIz7nZeHBqzPMlyHmy4X4lJ8vhpiOBjg/mGJfDn9OcDiMsZdEQsqHAWR8E7fchEu0yzOk3LrzkGTLY4qmQq2JlHmEMcSc/XnoU9dtcFI0TCooSW/25Uv+6ue9fbpRHTZVi32ru+25KWjbe5qlXbuz0KnockZJVzY5o8VOc3McnfeGvk0R23uz0pUcAg4Bh4BDwCFwBQKOkF8BjFaTIPPN8IUkzRpjnBFU9EUCTbeWbSJNok5LON1Svv6Nb7QHO6lnvV7jd7/9Ld7+5S+F6PPWT/qq0x99W4+O49LPggBplolHLoTL/hGrudA0Uihagw3J5EhdzrisiAbpp+TbEEr21Hjel4iYldchWGS0FvP2xMIdBrSa+3JgM6sajEck5hUmowizrMR4GOFikcP3a8yWtGwXWOeNhEOkC1RFH3OYdOED8wXPNQQwhHyIRZrjYDJCWnpYT2pkoxrTOMQkZgx1H3EQmLjqEsLQsk294dN6rzDOOUk55y/rtSSa9QYpbbELZmKz3a4Z2Q41du0QY066aNXO/p22yznbUfupng1WrY2Xe7Pm+tbdfVytQ8Ah4BBwCDgEPisCjpDfgCCJMy3bb775Jj768EN8+9VXxcWEt3cmcbxBKLZVkdyRwPNFsq0v3tDJWOb3P/0Ub7zxBl64f18OjL700kt45tlnhdyrrEs/CwLKyEizDL1u7eGWcIqEmHWVitGlxdjFKWvIozm8y5moxVxnpSNoyvqWyKtKEd4oGD3qqi3Wcg/0VsprD3HsIat9JLGPg7wSa/ZsUmAU1ZitEpxMA6yyHLNlijQvsFyncutnlhdYl5VcOBTmHrKykltC06LB6TzHcl3jfDLCyTjBwTDBwSCWMIrjQSxjJXGAIDCXCvXXybWxTL4ulw/1iLk+PHJ18qY5+qpXa6pWGZNqqd2bS/2NRItgm7kkuLuC8kL8+x27Ua/uxBaV60uZT0ZXo78VdDUu5xBwCDgEHAIOgcdBwBHya9CiZXy9Wonv9//7v/4Xfvrmm+KmQiv2/t6e+ILv+rq+RqU08abPPE3xyccf4+c/+xkuzs8lQgvjj5Po98n7Tbpc+yMgQB7W52L9LrKBZhf51+TMryJGzNfKjmj3+hv5VqTVICLa2JNnVqtJco1FvjEuLPAQA4gbDwVjikcBspKxzH2sxgXGUSPW7pNFKD7lDy6WWK5znJwDyzRDVWZCxrO6RFZ6yCv6ntdIC2C0yLFcVbiYpDgaJTgcj3A0HuJgPMD+GBiPQ0zgYRD7CBtYlxrrP86LkbYCnChhF64r8BpnnyupqeCvK98CRIqXN+g66V0arq57epouf5Auz/vqebgWh4BDwCHgEHAI7EbAEfLduEgtCTljjj+4f1/eJycnWK1W4rrCts/08jyJuEIfcoZG/P9++lPwMiG6tvCmTrU8fqYxPuedFeFr6ZQK9de60UEFmGreCCvGndeEdrRyTHp+zZRTif5wku+UbIyivtKtvEY10dQ2UC//MUqMcM/GDfeBYQTEwwB55GEcAWkxwO1VglVW4micYL5KMY19uVhoHPtiOU/zCkXdoBJfdw/LdYU0y7AiIZ+leDgY4HCc4XBCV5YcB9MCe5MYB9NIwicOIl8uNBI3mtAXtxpdO+dpMDALIET0rydBZ968DZFv19z2sX23QeS5CRFmb6tEKjYvbtImI2NlpdAbQMqbA/RL7a8XW5+GbZu3qr0u3exj5tPXf11f1+YQcAg4BBwCDoE+Ao6Q99DYJtk8gDlfLHByeiqpxBMvS3Mrp/Ut73V/pCzHoN9vUZbmIGfT4Oz0VHzJGZmFLjIk5hqt5ZGUfsGEDKm7vCgSqz652mC+l8W3KJf2pHbLrEWhpVDW1UJI1sYELNGyhLvHu82IprmdmBaNb7oVkaG7MUVmByEnGRfXEEtyI58xTBoMEg9VHGAvGQrRXkwGWOcVpkkohJxRU2bLTEIc0l+coRPXeY1lRkt5hXVeSojEWZnjIswxjnOcjkrsjyscTAocLAoc7MU4Wke4tTfAZBBhfxRLLPPJIBTvcYn9o3PW87BEWF1UbBvvr1WkJWMB2Sb0rYzSeHsw1p567Wtpd7bD1ua0olMmslvF3oRaVb0MpVVRr/qG7CYZv0HYNTsEHAIOAYeAQ+AGBBwhtwDxoCUv8qkt0ab1lIS8yHN5S1tdy+FORkWhDzgPbT7Oi/ryPMfs4gJv/+IX+OCDD5AXhei8mM3EGr9YLHBwcAC6r6gF93HG+GLIbhOkSxTrimVaue3uJFy2Sej3hjpTaIl26+dsh5BmwzbFKcPyauWh3USsy4bVTaLKachb62zKPjJFKat1WP3TDSknMeVdnSR+sbm1XuKXlwCGfogi8jHwRliNeNlQhGVa4sF8ai4cmpcmjvk8FReX00UqkViWFcMleiiyBmmdy8VCp6sCk/kKe+eMhx7j7sFQQibeljTG8YR+5gHGcSAHQOm70jDiEA8x6/p6eLc4cpG99TIr1n+NSCMxWoyIp08v0qYhbLhy6xgjenrKFD8Bsjc4nYr0oaE3/PaDtu5Zp9bslanv61NJk1J+s7Vf2pzfZk9Xcgg4BBwCDgGHwPUIOEJu8aFlenZ+jnWaSihC+fJtGvz+97/HgwcPpJ6W7dPTU3z4wQcYDYcS1pBfyVd94W9Dr9FVTk9O8JM33sC79+4JQWdscvqqLxcLLOZzIfv0U2fkli/XS9DsUal/ptX3uFMvuzFYSyzbjGnuUzetYUqCrrNnub6irOMpldMyUxJWvryG1/GQkNIZpNPa2Bs3B5GHKgww9AfIhzEORgOkZY1byxKztMTDRYmLVYHx2QrnyxRBuJS45o2XSvQWhkwsaEEvMqmP5x4mcYDTYYz5IhNCvlrlOJwmKNYJ9kYRsmGEURygSiLEDNMYauhGswINC6nr0QcWhc/nAwZdU6x7Sv/XAC5RQkcKMVdk9GNgQ9Ko4h7hbhg8XV/UoTJat50q179JbqMfx9h2ROn2pBM1cl3Z5RwCDgGHgEPAIfDoCDhCbrGiH/fPfvpTfPD++/jkk09Q2KvueeByPp/j9x99JET5rbfekls6//FHP5JDnSTjj0rIKUfyTdcX3vT58MEDY32vazRFIaSfPuq0oj+qzkff6s+PpOFLlwkOa/qvSwRsW8CaaDf4lxY07StsSd12I8tGeXt0wA6uxFMJKaX4NmXj2KB1HMpo6Q9KukdbMC3ltSGmoOOHlrseHFvCD3ok/B78yMMgDBCGAfIaiMIak2GNwaDEflpKFKDDdY7haIg5LeHjNS5WGebrFFlWIC9KFAybWDVo6gpNVcnDwGqVocpyXFxEWOzF2BuGOJwMMR3GONobYphEmAwZqjFAFNroK61Hjs2QxlrY5OGCFzIxBn/TgORcVkUB8m1BwOAgyNRst+umjG8fg3qhGCm38QsSVfW2rZcVlWbfjE7+Ne3bUr19kSY7h4196+p60r2stl+juyftsg4Bh4BDwCHgECACjpDbzwEt37/85S/x87fewjvvvCPkm02MiEJyTHcTWvho1X7/3Xflch8hBC1De7QPlHxdW32qlz1pfSdZZ0hEusd8uV+dG8fj4dAnQ5rvaSBHupEnbQtsl3v6LJHkSH1iLmVLKJWoK79kb0svRZGZEtdL67GxjJOYCyFvDDFX5ZSlpOnjy2eQZT/wUZKsB8AgaRDHJMwV4ijCfF1iOBiCt3yOxykeXqxwNl9ivlxjsU5RFiVqumtVNdZ1Db+ukK59VGmKWRJisYgxHoQ43suwPxpgVTSYjBIc1Z6MNWRUFt76Gfo2MouBmCES27Xx3wjfQsjphmNeXIlZDWv0JwU+4Jr1q1TT+OImw47Sl4r52voByWq5tMXyT7T/77QvqHmrcjPRgWTUzSZXcgg4BBwCDgGHwFNEwBFyC6aQh57feJ5lO2EmeWlJ1k6JJ6/k9eOMW+4zIPWX/nUtU9qNjvInbVUe1Tedatu1qVXU16eMu0cnVb1SbJb1TfXMGxVGUvMmcIs+dBjruHFXMYSc9vU2uIteZd/6pPcdWWhHNn7TJMADWqt9lnnJEC8d8rE3ijEZ1SYqyx5jmEc4uYhwPo9xsYiRpjmyjOckCnkY5JmGsmhQ5BniwMPFKsYgiXC6KjEd5Ti1hPx2VmHMWz9HkdwyOh0y9eQdMl658GUPgczQknMCIH7itizuK7aCSAlALJt/YWIlF55ufoVqt+AS5TabafC1pL3Fvpcx23B559tfRrqmq0Q7iX5ue6d13/syLu8QcAg4BBwCDoGrEXCE3GJDn+3DoyO55p5RTmit5vsP4TpCSzv9xfWmTqYbP8dfvX9f0JbHo0O7QVB6pq0daeoom7b1U9tvJ4nvdOgMlVZTA+u0nmWjyUi0ebHUWgu4DEsXDsryFlFrGW6tuYakmqKHuiXlZhyl78plI4qTCXseosaTGzizGpgOIfHJDycRjkcBTkcBzsaGlM+XKRZ8r1LMVg3W61IiAOU0uTcN5hlvpy1wkTUYDktclB7GoxznBW8UjXE8HcrlQsc1MEkCTBhHPfSQ+JtkXCzmvAWVn3XBhrh02JhfDSw5t08jgiXdcwiAZx4+pM6CvL3DLCtp3267gsP3N/4J8/0df0IVrptDwCHgEHAIfOkRcITcfgSeeeYZ/Jt//a8x4GHKIMBbP/uZxB7nQcx/7pcS8el0iv39fYmw8uU70Hk9yhsEa6PQ66dsTGnxhpwWSKBsvk98e2ra9n6ddpc6LWjaMfFeTSvJOuOSwrF5EyiptP7OQlcVivJPn94bimrmYvLq0FIJMTfRTroexvmDF/gkPuRynzAChg0wDiBRWfaiEIfRALeHPmbTGLPlAGfzFOeztbixnFx4OAsaLFNfbvwsqgZr3lpaNliuC4Rlg4uKrioxHqxr8IbPW/slJsMIz6QDHIxDHE8ijBIfe1EkpLwJPcSMyuL5COyDJ9dOP3LjN2/WLbjozwJcRO9xxlB3A1F/vf3tEQQt+Jf3gGOoBX67lxlp+6OwrUO2SD9X7ewu6+r20PToJLY1di0u5xBwCDgEHAIOAUfI7Wfg6OgIk8lELuUhMSYxv3fvHj766CNcXFyIn+3T/riQdJP8375zBy+++CK+8Y1v4ODwEIPB4EtuId9EmlSG722KsynF0jbp2dXDyggD68v385c1mxrty5GYN39Vuq9B80bKUEoJ7yfuKCTj1hreW5XyUXGOFgu9cWQxpxU7Uq7EXMipHHQ0biuch7iK8GIhD224xDowLtxl7CNPIuTjEKssxjKtcL4c4HwxwOkswYO9GJ+cJ5itC5ysCiyzCnPGMq8qrMoaVVngogCCIMeDVYlBHOHoIsV4EOHhLMHRJMbd/QR7wwi3xgOM4xAHgxDD0EMdehj4HhjVPJDHE1q8GzSeeTgxRLu2W2gfRgRE41u+uZMG3bbOGta1rNjrvnSpSmjN5v5JrYpsKdHHI9OTQiqgKVv6nft5Hc+lDgGHgEPAIeAQ2I2AI+QWlzCKhBy/9NJLODo+lljg7737Lv7u7/4Ov/zFL4SU7IbwyWuDMARdZb7x8sv4P//6r/G9738ffBj4Ml8KZNDsSA5zXel6rFsD+XaP1vzJ/tdpY5sSqW1ZWy/J5VmZGtvfEsS+BhI6Q8i71Iyl4xmLt1mh0aaE28yZFl7Ws5ehh6adSzI6TKs966gG4W5KoLF74PuoggajIMI0CjFNAhyOIxxPYxwfDnAwm+BiVeL35ynOVznuX6wwW6eoMrpw1VhXjJbSIKszhOtCXF2SKMBsHuFgHONsf4iDUYL5YSWXC2V7CaZxgHIQoIw8xDwASpcanpcQFx3jwEKXlvYhRReiqewZC5u0uG02oLU7p4jaarvjplY/Cm1fm2nL2skq2dbVfj6u6tB+vrTnJUEdwaUOAYeAQ8Ah4BBoEXCE3EJB31YS4enenrxZfev2bXz8yScoi0Iu8eGlPcfHx3KTJi/uoXWbX7f61dui+ogZ6hiPx/jBD3+I1374Q3zlK18Rgv7l9h/vwHscKtPfg66fEjjTqvZQKQm53d3LzIBa2KMvwxZT381SpfsBslWKfS19FiYoFLr3gelmasi2IaeGeJJR97ytmZUnDrMKamLv7iHEjCnjWTKu2rlUkaUFnRb1gGTYQxJADmGOBj7GwwDjSYzBeIh5WmE4WuNskWEYBzhbRjhZZlhkJRZ5I7eFyqVZVY1Z0YiuIsswX0ZYrwvsDROsslqI+SotsD8McTRJI9uf2AAAIABJREFUJB1HAYahLwdQY99HjAaBVyNo6FtOS7/FiGujG3sLqyex3WUhFnx79lMXvr0lujEt3qJPGTkVtQ8yilRPxa5tl+Ydsr1ul7NU9Lh9LmtxNQ4Bh4BDwCHwxUbAEfIr9pcuLCTMf/5v/y2ODg/x93//9/jdb3+L73z3u/j2t7+N555/XlxL9NDn9vf3FWrbapLuyXiMvf19HN+6hdu3b8t4fCj4sr8el750FG4TOYnSIVWdxs196uq7nlqnqbZoWVNTLyVRqjH5hIMLke9cUHqyQs7YiwybL0PYzBpYz0cAk1JGVLfxt7W+o3is0TXpwwPHlbwQcdVmmC3ds1lDrs88b9zkIcyYN38mkTwQMrQh/cNn61z8ws8XGT6dpThfFjiZ51jlJRZZgaKsUJQ1igaY1xWyvEaa1xglOeZpIXHLzxZDsZTfPRzi1t4Ah+MEe4MQUwQYMkxjYA6gisWcIRwb437DlSsZZyoOPpacc82CnGZseavYgtRuT+/OAJG1vzjY7juTSzpVqgNda1zqEHAIOAQcAg6BJ0bAEfIroCMZj+MYzz//vFjID37yE8RJImWScrqZ0LqthPwKNVdXe54QcLqoSKjDL92tnFdD84ds2cWrWHclEetPTjtTnnkt29soxcRr5Y0+a6oWMq7C2o0SStItKbfmbxJoUW8JJCX5NhoM4dZp2Z7Sasbs2k3ZEF6qokU6aHgZgSHCYUD/8AaTiiEUPawnEfYSX2KYH44znC1yfJyshWyfzNdY5wWWeYmyapCXNTLeALqmJT3HMi8wSkJcrFMJvXjBi4bSArf3K3GRORiFmEY+xrzciK40XiOHURkpJvRpGSdWZsa8kJNr5e2n/ZciuFXdF2nz1mPdlNnxyk5qklftVsWV8u0QLuMQcAg4BBwCDoEnRsAR8hugk4OXYSikmRetMCQiLdr0Mx+PRi1puEHNzmZaw0nGnYvKTnguVT45JzI9tyhWy5/7A23L9Jlbv02t36JZfCFahmx8LVql2qs/eyXmrZD9HBmLuOXh6uxCl21DyO2M+5qUlqsmYxnXMTl7zdNszp5K0I3LCy3PDLsYWQVeYAjyMAhRNj72Ex/rvMbRqMDZ0li9L1Y5poMQi7TAxbpAWlQ2LbDKczkAuigyhCsfF+tIDn1epCTkOc7XGY6niURj2R+E2I8DTCK+fUwjYzHnw0AQcH7ixCIr6B+B1ccWxUnXTkGzwramx7sVNcVDZbTelrebVWyjvndIQNt7I7VVLuMQcAg4BBwCDoFHRMAR8muAIlEeTya4fesWvvu970kUlq+//LK4lzAiCw9kXkemaT1n2ET628qNn6RDtJ7qBUCMsuIs41fsABmQkiUlkUZ0s7TZvd+r7b/l6sAeG/zqmnI3AzuOJcf0dZYX2TJfkti8duqN0s25R8ZbOZMRmbbOqBTLro5pRrrir45Assh58PCoId3s0Kllm9bzs2jt8qZa3FhIdKmtoVtJ6CMvaTEPsW8v/6Ery2QQYJ6WOJ1nEo0lnq0xW9O1pERGN5aqRkWi3lRI8xxFWSArMsxXDLUY42wc43AU43BIF5YIB8MYR6MQ49jHuPERNyTldKkxlnJrLO/W0S3I+Jrr7wt2C5iYg6Ld2mXVvX4s6zZeAWpXbfVe6qD1naTJteO0mW0JV3YIOAQcAg4Bh0CLgCPkLRSXMyTOt27dksgnBwcHWK1WYh3f39sTy3bfXWWbmJOI82Kh1XJpbkDMcyHmJOc8DEr/cYY3pBuMi6qyjb2yHEMylT5uS22Xu16bLVqvtVrWVOv71IltLG/LqFW2PRvYdraSkmgvq7GvmPJtdY+cd5WthV3JeH8SncW7+3HGDGnItbTr5Hrqt6cg024MGWd/JeaiqyXkgB8AMUk7D33KTZzAKo8logoPeX56notLyyDycL4EBlGFde5jxZs/ScrrGlVVYLbIUWRrzC5CnA5D3B9QxwCHoxEOp0Mc741w92AE3vi5P/AxiHwMYyAKGsShcWMJG+P33u6BxV7XpstuIdZtkPVZKXZWFq7t0tRqsVptIuBsVklpoy9rLlXs6OSqHAIOAYeAQ8AhsBsBR8h34yK1JNmj0Qgj60+ek1RXFdI0lbcVEis3/cnV/YRE/N1335WLhe797ndYzOdCyknGeesgD9INhkO88OKLePnllyVyy/7BgRDza6bzpWvqk0+zeCVNHRRKg1ijrf26TrKjTKy7Sma77Sq5tl4HbUencwVfvdnzhkpby0Q4oZUxiWmVQ6hWUPS3Fu7O+s3mdmy7ZkNETYuMpIy1h4kOrzMx+k2tDNk07VVFHEAfMBmVpfaBKPExikmSfeRVg/1xhFVe43Cci+vK8djDxSrGg1mMZZbjbJlhlRWYrVKkeYE042HQFOtlg/k8xEkUYTwcYjLMsD/Ncbhf4faKt4rSch5hFIc4HAeYJD4OR8AoCjAmMZeDqOZBQn3KjWNLF5GFLjh88ccLrk3bTS3/KgpdzSaqtr4PdF+0n9+QEST7rdfkNzoaOXVfb3s9jr620x9l5ouzkj9KeN2kHAIOgS8AAo6QP8ImkkTPLi7kgqDCWrr165TEJQpDPPvcc3LIk+poSf/Fz3+OX739Nn70v/83Tk5O2ouF1GWFrip/+md/hr/+67/Gt159FcPRyF0I9Ah70RfRPejX7co/qZz2u4pMSPt2o0ZEEeLcNXY58kFD1k1d729PiNnWV7q3qJ7IZQ7ZMX3To3V17vdivl/mRBvjSsUF2SZSVnUT0WvvSYajIEBZA1HoIU8ajCIfaR7hcOhhvo5xZz8Wi/mD2RrzVYb7Zw3m6wandSa+5YzMsi4apFmDZe7hLANOcg/TzMf91Md4UOFgXGASB3j2gOQ8QFEDRyO64PhIAg8JA6pznn43R10V03bfWt97A4ddmi6xh+qOrCrZ0bS7SrXvbt2s3a18d+1mT1dyCDgEHAIOgS8mAo6Q37CvWZZhvVrhzZ/8BO+8845Yxmnp1he/huln/n/9+38vccQfPHiA+/fv440f/xjv/PrXeO+998RC3ndv0b5v//KXYl1fLpdiHb9z9257MZDKuJQIKFV5HNJjkNOeimO//PjaVEtnjW0ZbG+WOobatdmrP5YSXcr16/tyrOebVnOVNzDs6tXNq6+x093lLg1Idb13O5Y9/KnzoM+8HAD1jZWaDwuFDyQ+b/8EJnGC9TjA8TiyFvMIs1WG/QSYLSPcTwKJa75IS6QlkJUe8sbDOquwaAqclCmGWYAkqXDICCyJj1lGv3IfaZZiPg5xZxxhyAOgSYQ4DBCFgfiYMyoL5+N7PAZqH2QaEyrRYNhHpY/VFXni0QIlhc4/qN/FNnVVPR+hDR2dRJvrbUn3+dbWrvHSECryhGmn+QkVXNOtP9d/znGumYJrcgg4BBwCn1sEHCG/ZutIotfrNU7PzvCjH/0I//N//A/xCecXDy3ctI4z5WVBDIXImOK//qd/At1U3nzzTXz04YfSfxcZ57AfffQRTk9PUVYVDg4PRRfDLbpY5Lopn+0rvt+bGrfLOspN6a5+WtemrbtB56qibdTfJyia11TH17KmnLEeTOzIuEr3FiQdbK/WXaXT0uuxM6vzZI+ul6k1ZeYbIbssc048ixz7JlRhDQ/TKEJRhViNYolTfjCipZyE3Mf5coC9UYIHswyniwLn6wqztMKiaLCuPGRZhbzI4eUB/LDCwSrANPaxTFMcD33kaYDZ2Ee2P8BkEOFwMsQwjiVWeiSXDPlyOREt+Prig0X/F4b+GlXmyrSnR2S6p5SuiyrsanrobSvYENoq7FQkMtst2+WrRnlUua2JfKbi9pifSZnr7BBwCDgEvoQIOEJ+zaaTSPN2ztOTEzx88EB8wumO4vm+HPZkpJUXv/pVPPvMM+ITPp/P8ctf/ELen3zyCWj5voqMc1ha3/m+d+8eXn/9dQRRhNt37kj8c/XhvWZ6X/CmJ/+KJ1G5qfdVZOZGUG1H9ULmOP2xtsuqT2V0bjvHVyHbqS/T0XzV2ON/QqNVejvtyXOm/F9ryLUDShet7CzyptUEHOQ5SCMmnu5CypkLfFqiG4QhEPkeQj/AIORlQ4FEZZkkocQtP9gb4+Aix8N5jpNFjodLhkAscU5iXgIrEvO6QlE0mDceihzwigaLuEG+9nA68jBbjrA3jHF7v8R4kOBwOsIwoTU9lDEZEYbW8sjzIddr9Uh5f5foc8+1mJUoXsRzawN6jyd9FJnv9bKqLX6iYqPVtF/STS398fr5rqVfK7HZexPpt/WqN7JmnRtV/2yFq+Zz0xwMWlf13jXdLXx3ibg6h4BDwCHwOUPAEfJrNoxkmqT67PRUXFVYZoSUKIrkgqDnnnsOf/Xv/p3c2sn45LPZDL/61a/w1ltvXemmosPRsk59fN//9FO8/uMfS2zzH772mritOEKuSD1Zql/Zu77mte3JNF/fa9d41/cw5O66ORkyfpVm9tTe2+l1IxtW2vbQjO3C0XRccZtRFmst5WyXelrM5SIkz1jOAx8R/bzDAOUgEgK9Kivs75XY28txMCuwN08xnqWYLDKMFoxPXuEiqzErG2RNhbqsxN+c8RYXfon1EniYeDhn/PNhjGfTGtPRAHeKBpNBjONJgkkSgHHNB4GPJmzksiPeRmqWZZ3JZW2Ko0nNOnsQtus3PfXBq0OyB9Smqk5Ec9rOcjtQr7FV1Rfsk3FTb0JQmn6bkqprM23V9qq17tI0ejKfJfso87pa/2frfbVe1+IQcAg4BD4/CDhCfs1ekSzTQn52diaEnJbxr371q3jmmWfwb/78z/H8Cy/gu9/9LibTKT784ANxUeEBTlrKGfZw+0WSzQgrURzLBUNZnmM+m4lbC33P6b7C8ej6whjnJO3uRQRIJ5RSdIhcruna+jn9ut+W3y73+9yU7+ukHi0/yo5RXsfWlON1eUsDO6N1v9FOra9ls3d/7sYKvFkjJbrY7LTamol4jT0nISFcSN41rKLVJXMzfjq03FIVo57Qj5suLFHgS5QTcSmpQ4RRjCiKMRqUmDIG+TTB6SKXNy8cOl1mOFkxEkslt38WZYmqLpFWNR7WwEXpYdZkGK0qnBYepkmGh6tSCPoz+yOJaX6LxDwOsJ+EcvhzFHiI7K2ftJi3/uU2yjpX0mGuBVvTOxC6EyZuuLoH6ebrrwgCka3UNn5CdDBN+3IWVkm8btfYvX9ipVXXk9e6DbW2nW39euZVvqfiqWcfdYz+3Mwkrut5WfqpT9wpdAg4BBwC/0IIOEJ+DfAk5CtLyOlaQt/ub3372/iTH/wAf/mXfynEfDQei9vJJ59+it8yxOFisdNNhWScYRGn0ymmkwmee+EFidryQV1LvPJ0vcZyscB8sRB9cRxfM7MvQ1P/y/dRaO5lTKiB747Q7Ja5XPtkNRzrOjrR16qr66f9PGW1bDIsqXbm9d3X2ssLoVR5W98yy8ZwyXYAtu+WNaN0TwbaxaRaD9SMeCKk1xByknRadv3AB+OHM555FIQ2ikqE21mC81WB85W5XOjkIsWn53Ms1ilOlw2WWY2LAkgrYFF5qBrgfFEiTmucpA3GUYoHi0IuFaKeW5MBVlmF/WGIfBTJBUNlZKKyDMMQMd1p+LDABwtLyM3a7NFb8RPX1Rm8BBHl0RYeleClS/JS2DQ1tZtwmriUO7as10nUmbLWMjVvHVWVa/3mFCjFN/tc7tH1/UPldA79+fTzl+fBVr40tcU2UY1thcs4BBwCDoEvDAKOkN+wles0FSt2nmVyiPMrzz2HV199VSKq0JJdFAVIpn/z61/j5z/7mZBsEvn+i5ZuurncuXMH/8df/iWef+45PPPss/j4448lNCJ9yD94/33Rw4guJP/0T//yvvpfvJrX9NHJhu5C1/Myote1XZa+ueZx9PVlmW/dI/oNO4c00qbpRmGrwTDL1vaqVti2u0HLFPt5nUAr2CN7DDtIWXPJvbpWcB18CKJvuQ8euASGvHUzCeTCH3EvKRlnPMYiqzCbxjibxrgz9jBPYzycR5ilBT5ZFbjIKtxPa8zLBquqxqpqkOYZEt/DMi0wjkIs0xwn4xizxQAHg0h00a/8eBRLPPOD0QDjOJKxQyHmxlpODs5VSVhHXWab0p3McENNKatvinWItJ1MxsDXVe4S1P+PkDbb4VI/NpoHBmnqe9502m3OdOZf08tUbw8t7duVIrqz8tIoj1NhZrQ5n+3+Ot/teld2CDgEHAJfNgQcIb9mx0ms8zwHSTkjofAr62B/H3d5iHMwEEs4D3men5/j3Xv38Nvf/Eas3NuEnJZ1Wsaff/FF/M3f/i2++c1vSlSV9+7dE32UZ0SWvCiEjJdFsdPKfs1Uv6BNShI0fXrLfFoan1TPdr/t8s6VarQPtc4qJdzufInlGGokZFyJOAdoLeY6mlKoHtm0uo3o9kCU0zqmvby1LLOGv2/QOi23foYeBo2PUcPwhTX2BzUOkwCHgwAHAw/LNQ9rJkLIB7McD1YlilmOalWgSgv5d7guK2RNg7IsMPd9VEWGxSLEaplgbxBiNomxP4yx2OMh0ESs7IdjYALjY57w4cAe+OyHStTZCxoWCv7bpPeOQCo3m/Zin3c/ELQrl74bihTbftrh/KjWYKqUOVg1/Xxfhw6taX/Uz2d+c6WfzzW4WTsEHAIOgZsRcIT8BozkC9kevmy/Rmnd8jxxNWGccRLrT+/fF99x+r5uE3KScV4CxNCI9EE/vnVLCD0t7Ldu38Z0b0/8xXWsG6bkmh8TgX8OcvI0dD66ji3JreIlOHa062d3O+36WtcNW6Fyl1WxpV/bz9s2dfPoSZKU83miTZkPfUSeh9iHREnhTaDrIsE0HWKZVxidZzheFkgGaxwuMpwuc6R5iSxLUZUlUOZAWWKxyFGugXQVYBwHmA1j8S0/XaTYHw1xJ61xPC1xMEowTkKMk0DimScc3/qZywODfXiQhwy7LD7EcFX8J8+bP8WXXjDiRUVmURRtPV7U8t0Bu4GWVLdEngrsq8Wse8TRxx0jZY7YUrrXS3u3qUr1d0V/CWiFON9+YaukTdeNozKaburT2idNd2nbVfek+l0/h4BDwCHwx4eAI+Q37AndTXgQk5Y0vhiXnNFU1Ff8t++8g1//+tc4efjw0qVBlGc/Eu4f/umf4rvf+54QcFrXRW8YSrhE+otLVBV+mZP83zAn1/zHh8AfM13QzxNTzRNB5s28+7U3YXvDSkksVZ0l4CzShYU9e00Sy5xEOPJDDMNAQhgWTY1pUSMtGwyGKY6WOZIoxNEwwoNBhlVWYrYAeCB6tSpQFBXyvEBR11itG8SBj4skwiiJcbYusT/OcZEDZ+sKR5MS+6ME+6MY0wEwGfoYRnwY8JDwjIdY8u1DQ2++On8ugHmzBl2JWRcjurBls40POeY/SglyPTJ+GUnW2EEoJ8ps3da2sFZn0OppgTdz0i67NWjrZ0/b8Z9A1c19b5Z4gmFdF4eAQ8Ah8EeHgCPk12wJSTJ9uY+Oj4U4M3IKb+xkFJWvf/3rCIMAP379dYmwwkgscoNnz0JGV5XhYIDDgwOJyMIwibz4R6On0N3lwf37uDg/b6Oy1NYaf820XNMjIvC5+yq/NOFLFY+48m2xXXpI51ivKfsYiqe121racusy09bY20S7cchPSUcZeYUvUzZ5VglN9SDxwhlMiIR24AeI4CMIGoyqBn4D7CcBpqGP871E4pcvsxIPzgMs1xkeXtRYpR7mqwZ5UaKoauR1g/O8xrIusUaG05Rl4P6iAH3JDycDHI4HOJrwnWBvGGKS8GKjQA5+JmIx5wFQ41tOB3Ox7NuTwUq5S/13LiEfzXoM46bnPF/mFwdZvkdfeiXmBnWDQYdHe8pWLOUWNNNs/orSbn/MCFZAxE1bfw/73Tm3Ta2mpL36smxhvcqrjJY3xu517Lf3qiWrOrbrN8vXadiUdCWHgEPAIfBFQ8AR8mt2VKzb06ncxEliXVcVfv7WW/jdb36Dl77+dQySBL9+5x0Ji1jkuSHkPX2MqrJ/cCBWcYZKpKsKD3fSNYWHQc/PzoTMM9whyTwfAOTd0+GyDoGnh4ASnsv0iC36vna8HWTcyHeEkyJaUnHq5qhqKReSy46eCZcYsIcHiR8eeg3KAIg94DDxcRQHSPMEDI+4yEp8nAAXywjToMRs5eO+12CR+VjkJfIKyGq6vjRY1gWitMZ5VuPhosR0kOFwnON4UuLOfoVF3uBwFOJwFKAYhBiFvri80JWFxJyXDPH/Azgvvjl/cStjSr9yS8oNquavYbFcpcWYvvM2orvBl8hYxKybSkvWFSw297ZIDN8sa0ftb9NOWGZolWvjVietviK9Svqm+qvarxjGVTsEHAIOAYfAFgKOkG8BslH0PIzHYxweHSEZDORbmVFQGHGFkVFIuHmgk2X9cu73Z0hEuqnwTSs7Y4uTcNMyzgOgtLa//sYb+P2HH4rVnPK0yHMsyrmXQ+CzIWA+Q90nybA89Rbv6jtKp3WaXj9+Ry7VYGz6db3VMq6WZbYY7w5PjMLW8Cxck23yJjH3gCT0UPs+Jl6AMvKwF3hYFz72ggkW0wRHowCzLMPH52O5NOj+IpOoLbwBNKtqZBVdzBvkdYlVmWOWNpita5wvS5wz7vksxdE4wsEwxJ1pgukgwtGYlwyFmA58icoSh+YAqPn3qDPkQ4SZP/ExczbsusejW/5Mnt0+iIi8iduuAnVjLlVqsba8mnrlZYm7CfvSq9SsCrVlnUVnFteaPqtnXTsGnwA6oV59q3RnHVtVh6ZdD6q0tbsarWAr0+94Tf4aVdf0ck0OAYeAQ+CPGwFHyK/ZH34J89Kf46MjQ5TjWMh3XpZ4+PChfNXQxWTzi5LfUJ7ELOftnd/7/vflMOdoNDJW8fNzPHzwAK+//jreeP11/PLnP5d6knCSf/qbq4/5NVNzTQ6Bz4gAac0mJTPUSlmZplcNs02LtNwj6ZassUVtxipFUt4nqULSe0OxHNCVRR5MffFtGftAXnmYyuHPCgd7sVjFj/ZTPFzmGJ2tcL7MEZ2vscgKuQE0rxoUNVCmFVZeI7HK56sCMx4SHawlbvn+MML5wQj74wTPHNQSoeV4ypjpAcaJjyjkRUeGNIu1nHP3TTRzPUQZWP9tffBQmmos69bEzv/HaEwP4kDLuHmZMJEMvyivloBrK1PSVu6J7ksv1az2l3G6e4uMFv7V2XY17CrdVEfX1OZatW2Nrq6r2CXTtbqcQ8Ah4BBwCNyEgCPk1yBEMsAIKXRVocvJ3bt3xdd7uVyKi8lV32H8mXsyHoury0tf+5rELKdl/dNPPhGrOGOOv/322/jggw/EWs5DnXGSCBGnj3l7yPOaubkmh8CTIaDUyVAx/Qxr7Y06VVA6asH2UmUbSvqVVt4abllSIk6pvjbmAxJTIadGx9CnG4uPMPDFxWQwSrCuGoxHBQ5XOcbDAc4WGfaSAS5WuZB0Xha0zCpkRYWyqlGVFZZlhUruD/AxX0Q4S0Ks1hWmowyzVYmDcYLzNMbeKMDBNMYoCTAZxELKGcdc4pZ3S5F5s2jIOldkbL7deqTVEmLzwEKruVlVJ8UoLlKSP327sWJob/+VnyO0zoLddTQVLMvDjBlHtWm6sUWdHVuqRdWmwNbu9MfuS19Vv7m3fdX9Hv36fr4/Qr/e5R0CDgGHwBcJAUfIr9lNEnJarXkI88WvfhUvf/KJWLPpnsJoKzzkuf3iQU4Sah7gfOmll/DsV74CuqJ8+MEHEqv8//lv/w0MlfjJJ58gS1Mh9iT9R4eH2N/fl0Og9DM3lsFt7a7sEHh6CFxPhq6iQVrf792yy8uTU58UtmhXm2dRq9Ra3lfANh7s1OAhse+Lm0vo+eIykngB8gYYJBX2RqVcAnQ+yTGJErGUT2Yp5usCp4sM83WGdV6iKHkzbg0TyxxYBSXm6xBZUWO0jMSyztjlszzB/iTC7XKIvVGEw8aTUImDyPiWy6FPPjTYSDK0mJOKk277lwh5n6LrirtfCPShpG1hrHhCWlOf/gJHvPWtvzdYtNqO1KTaOiRJwpWIb+1aJ7St6lKLVvQ1aB3Tq+r7Mi7vEHAIOAQcAlch4Aj5VcjYepJx+n7/yQ9+IAc0mf+nX/1KSDUt5X3fccrSNeXg4AB//bd/i2+/+iqmk4lEUvm//+t/xW/eeQe/u3cPs4sLuQBIorIAuH37Nl577TWJ3DIYDh0Zv2FPXPOTIqDMjeRJ8zt0CbdSgrVDTpukqyHjRqqT7avo/xvp5DolrCON1D4io9FLeCiSYVh6VmE+rDY8bEmLuRBgH4OAl/4McTyKsB/HmK0LHI1TsZR/er7E2SLAbJ1jlVdI8xp5WQs5rxpgVZaoVg2iPMMiz/D/s/emXZIc15Xg9T32zKwNC0mAJECIBKl1qG6BLR196NFIv2D6n/Z807eeo9aIEiVSAiluEoiFqKpcYvXdfc59Zs/dIzKyUIWlQCAtAE/bnj0zux4Vcf3Fs2fjOMBllmAxjXGRTrGYJXipqDAbhXLwEMMkjqMQET8bQkZk8cSaT0iFEstGToMw19Sv1MBu/O2tpZzt9omDNJv9FcWWTyPs3RgC7oEGANYdEnI+AvClTy+
variable, nonlinear
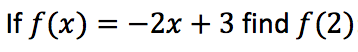
f(2) = -1
Which table represents y=x-1
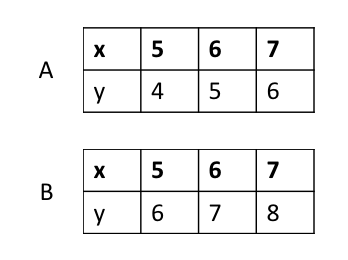
Table A
Would this be a linear or nonlinear function:
I started with $3 on week 1.
Week 2 I had $6.
Week 3 I had $9.
Week 4 I had $12.
Linear! Increasing by $3 each week.
What does this graph tell us about the situation?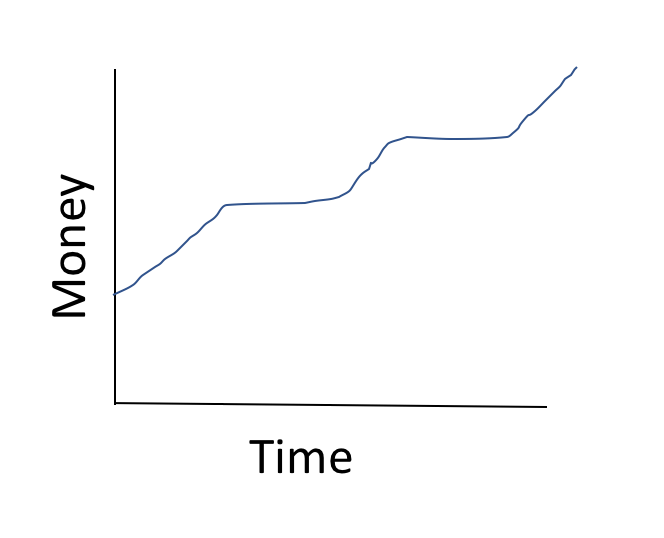
It tells us we start with some money already and the amount increases, then stays the same, then increases again, then stays the same again, and then increases more over time.
complete the input-output table for the function y=3x +3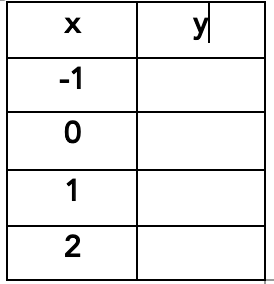
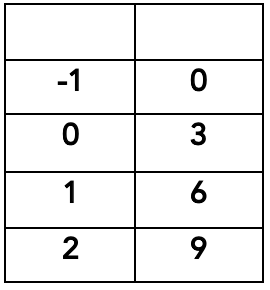
A baker is making cookies. Each pan makes 14 cookies. Write a linear function that represents the relationship between the number of cookies (C) and the pans used (p).
C = 14p
Is the relationship linear or nonlinear? Why?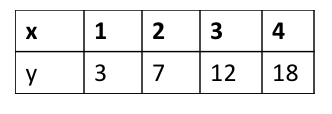
Nonlinear! The outputs have variable change.
Explain the relationship between the quantities that is shown in the graph. Possible reason for the change? (And is the change constant or variable?)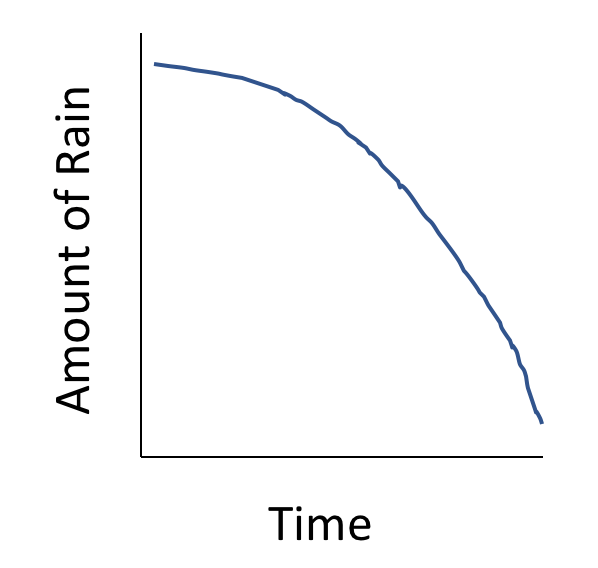
The amount of rain is decreasing slowly at first, but then it is decreasing more quickly. It could be a very dry summer, or a drought. This is a variable change.
State the domain and range for the following relation.
{(-4, 4), (1, 2), (0, 3), (3, 2)}
Domain: -4, 1, 0, 3
Range: 4, 2, 3
Write the linear function for this table.
x -2 0 2 4 6
y 5 4 3 2 1
y=-1/2 x + 4
Which equation(s) are linear and which are nonlinear?
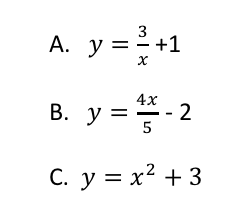
Linear: B
Nonlinear: A, C
The amount of chocolates I eat each day increases at a decreasing rate. Which graph best models this situation?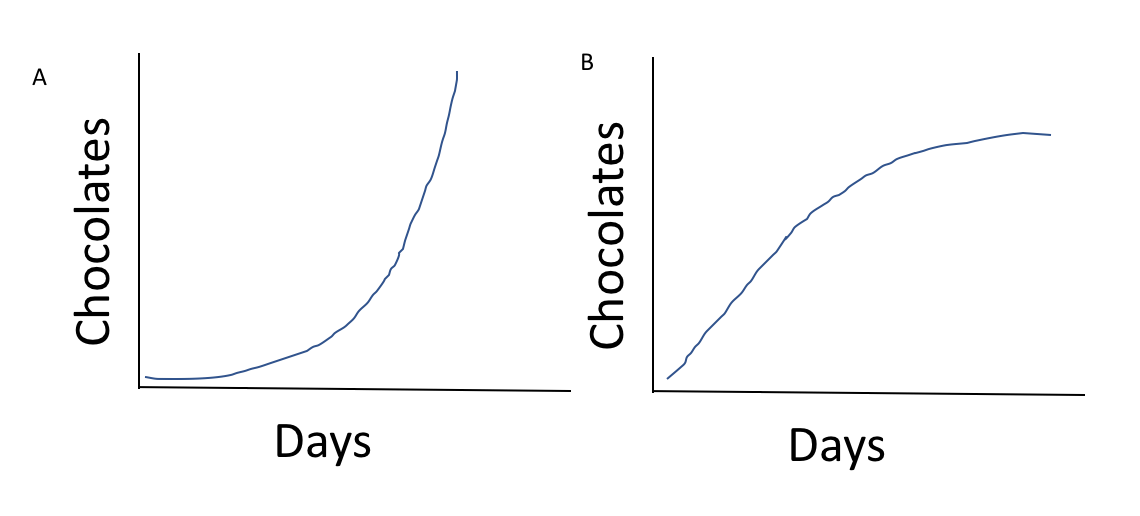
Graph B. Increasing at a DECREASING rate (slowing down)