Characteristics of Functions
Domain and Range
Evaluating Functions
Average Rate of Change
100
How many outputs can an input have to be a function?
one
100
Domain is the ____ value and the _____
x-value, input
100
f(x) = 3x + 1
What is f(2)
f(2) = 7
100
How do we find average rate of change?
Find two points. Use the slope formula
200
What is the minimum coordinate point?
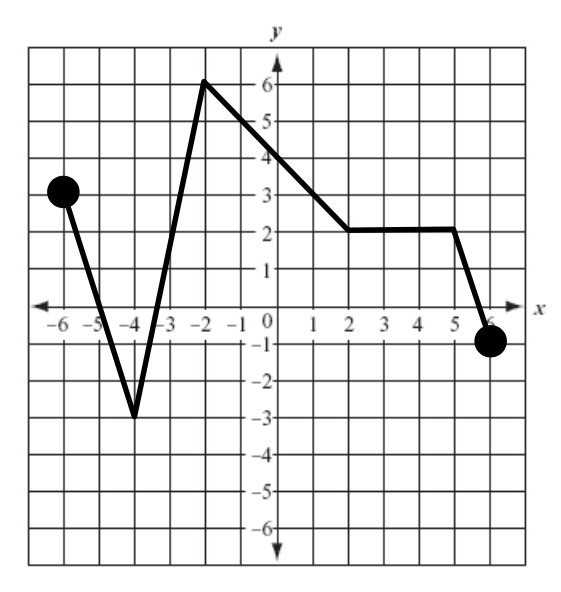
(-4, -3)
200
Range is the ____ value and the ____
y-value, output
200
g(x) = 7x - 4
What is g(-2)
g(-2) = -18
200
If I travel 20 miles in 4 hours, what is my rate of change?
5
300
Where is the graph increasing?
between x=-4 and x=-2
300
What is the domain of this graph? (use interval notation)
{-6 ≤ x ≤ 6}
300
g(x) = 7x + 4 and f(x) = -9x + 2
Which is greater? f(-2) or g(-2)?
g(-2) = -18
f(-2) = 20
f(-2) > g(-2)
300
What is the average rate of change between x = 1 and x = 2?
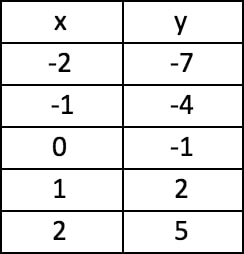
m = 3
400
Where is the graph negative?
between x=-5 and x=-3.5 and between x=5.7 and x=6
400
What is the range of this graph? (use interval notation)
-3 ≤ y ≤ 6
400
Evaluate f(-1).
f(-1) = 5
400
What is the average rate of change from x = 0 to x = 2?
m = 3
500
Where in the graph is there no movement?
between x=2 and x=5
500
The function h(t) represents the height of a ball after t seconds. What represents the domain and what represents the range?
h(t) represents the range
t represents the domain
500
Which is greater? f(1) or f(-2).
f(-2) > f(1)
500
What is the average rate of change between (-4, 3) and (8, -1)?
m = -1/3