Functions
Graphing functions
Evaluate Functions
Linear Functions
r-value and linear regression
100
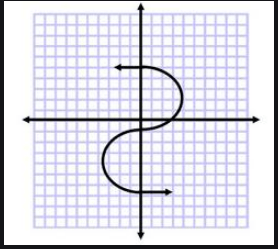
Does this graph represent a function or not? Explain.
Not a Function. It does not pass the vertical line test. There are x-values with more than one y-value.
100
Graph f(x) = -2/3 x + 1
100
Evalutae h(x) = 3x - 24
for h(-2)
-30
100
Write the linear function.
f(x) = 6x
100
What is the r-value to the nearest tenth?
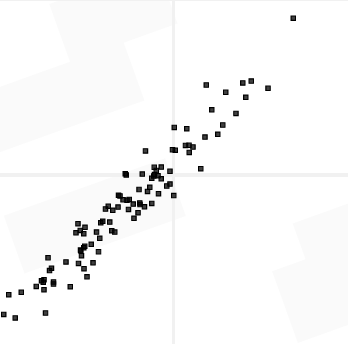
r = 0.9
200
What are all the values for x that would make this a function?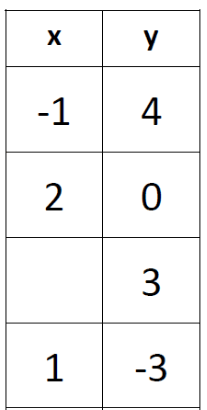
Anything but -1, 2 or 1
200
graph f(x) = 5x - 4
200
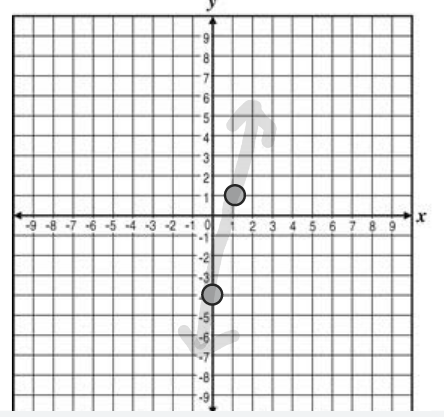
Evaluate the function t(x) for t(3).
4
200
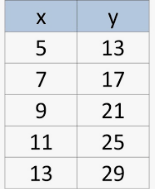
Write a function for the values in the table.
f(x) = 2x - 7
200
Describe the correlation (type and strength) if the correlation coefficient is 0.857.
Strong positive correlation
300
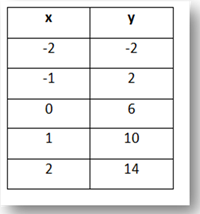
List the values of the range.
-2, 2, 6, 10, 14
300
Evaluate the function p(x) for p(0)
4
300
What is the linear equation in slope-intercept form of this function?
y = (-1/3)x + 5
300
What is the r-value to the nearest tenths?
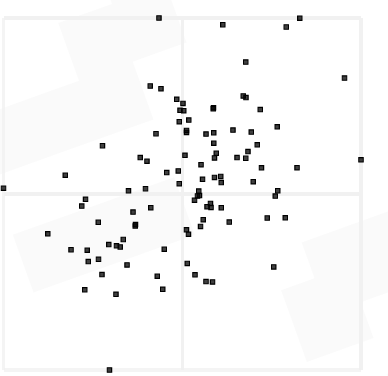
0.4
400
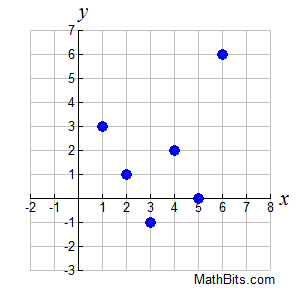
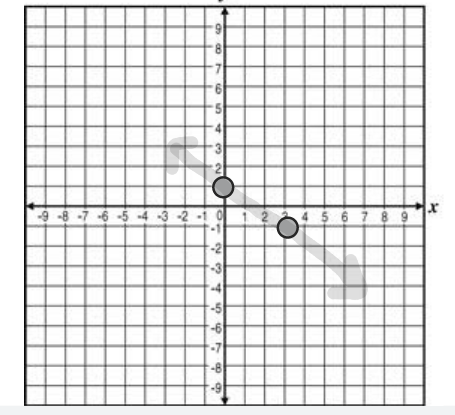
If the ordered pair (5,5) is added to the graph, will it be a function or not? Explain.
Not a function. There is a point (5,0), so (5,5) would make it not pass the vertical line test.
400
Evaluate the function for f(5)
f(x) = 2x2 - 3x + 7
42
400
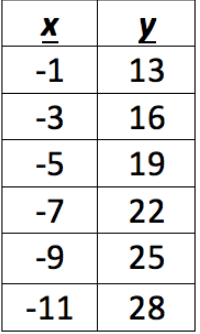Write the equation in function notation. Leave numbers as integers or fractions.
f(x) = -3/2x + 23/2
400
Find the linear regression equation that models the data. Round to the hundredths.
y = 1.88x + 82.65
500
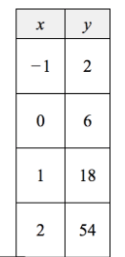Does the table represent a linear or nonlinear function? Explain.
Nonlinear. The pattern does not add a constant amount in the y-column.
500
Evaluate the function j(x) for x = -3
j(x) = -4x2 - x - 1
-34
500
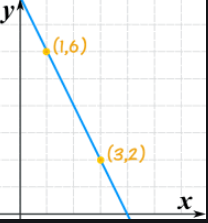
Write the function given the 2 points on the graph. Then evaluate the function for f(21).
f(x)=-2x+8
f(21) = -34
500
Anthropologists use a linear model that relates femur length (x) to height (y). The model allows an anthropologist to determine the approximate height of an individual when only a partial skeleton is found.
Use the linear model y = 1.79x + 84.3 to find the height of someone with a femur lenght of 54 cm.
180.96 cm