Function Notation
Domain and Range
Inverse Functions
Transformations
Transformations
100
f(x)=x2 + x
What is f(5)?
30
100
4) non-negative rational numbers
100
Determine the points of the inverse relation of: {(-2, 3), (0, 4), (2, 5), (4, 6)}
{(3, -2), (4, 0), (5, 2), (6, 4)}
100
Describe the transformations in the order that they occur to the base function f(x) = -x² + 2
1. vertical reflection
2. shift up by 2
100
Given the parent function of f(x) = x², describe the transformations in order that occur to the transformed function: g(x) = 4f(x - 3)
1. vertical stretch by a factor of 4,
2. shift right by 3 units.
200
For f(x) = 1/(2x), determine f(1/4) + f(3/4)
8/3
200
What is the domain and range of this graph?
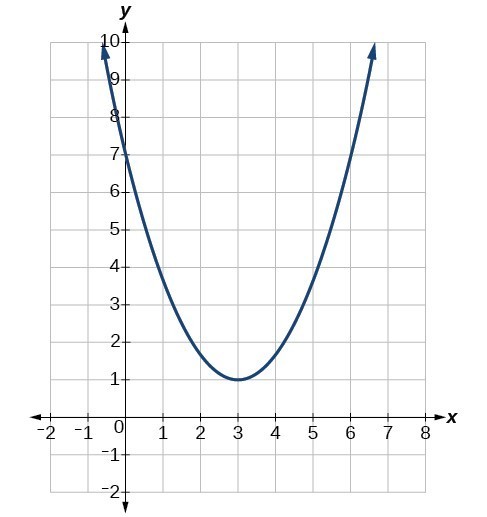
D: {xER}
R: {yER | y≥ 1}
200
Determine the equation of the inverse of f(x) = 6x - 5.
f^-1(x) = (x+5)/6
200
Describe the transformations in the order that they occur to the base function g(x) = (x - 3)² + 1
shift right 3 units and shift up 1 unit.
200
Given the parent function of f(x) = x², describe the transformations in order that occur to the transformed function:
g(x) = 0.5f[-2(x + 2)] - 3
1. vertical compression by a factor of 0.5
- horizontal compression by a factor of 1/2
- reflection over the y-axis (horizontal reflection)
2. shift left 2 units
- shift down 3 units
300
For h(x) = 2x - 5, determine h(3c - 1)
6c - 7
300
What is the domain and range?
D: {xER}
R: {yER | 1≤ y<4}
300
Determine the equation of the inverse of g(x) = (2x + 4)/5
g^-1(x) = (5x - 4)/2
300
Describe the transformations in the order that they occur to the base function:
h(x) = 2√(x+1) - 3
1. vertical stretch by a factor of 2
2. shift left 1 unit
- shift down 3 units
300
Given the parent function of f(x) = 1/x, describe the transformations in order that occur to the transformed function:
g(x) = 2f[-(x + 1)]
1. vertical stretch by a factor of 2
2. horizontal reflection (over the y-axis)
3. shift left 1 unit
400
For f(x) = 3(x - 1)2 - 4, determine 2f(3) - 7.
9
400
What is the domain and range?
D: {xER | -1 ≤ x}
R: {yER | 0 ≤ y}
400
Determine the equation of the inverse of: h(x) = (x+8)²
h^-1(x) = ± (√x) - 8
400
Write the equations of the transformed function:
The parent function is f(x) = 1/x, is compressed vertically by a factor of 1/3 and then translated 3 units left.
g(x) = (1/3)/(x+3)
g(x) = 1/[3(x+3)]
(a = 1/3, d = -3)
400
Given the parent function of f(x) = √x, write the equation of the transformed function and describe the transformations in order that occur to the transformed function:
g(x) = -4f[-2(x - 3)] + 1
g(x) = -4[√-2(x - 3)] + 1
1. vertical reflection (over the x-axis)
2. vertical stretch by a factor of 4
3. horizontal reflection (over the y-axis)
4. horizontal compression by a factor of 1/2
5. shift right 3 units
6. shift up 1 unit
500
Given the function f(x)= 0.5x2 + 4x - 8
Simplify f(-9+n)
0.5n2−5n−3.5
500
The function h(t) = -16t2 + 144 represents the height, h(t), in feet, of an object from the ground at t seconds after it is dropped. A realistic domain for this function is:
1) -3 ≤ t ≤ 3
2) 0 ≤ t ≤ 3
3) 0 ≤ h(t) ≤ 144
4) all real numbers
2
500
Determine the equation of the inverse of: k(x) = √(x + 3)
k^-1(x) = x² -3
500
Write the equation of the transformed function:
The parent function is g(x) = √x, there is a reflection over the x-axis, a vertical stretch by a factor of 3, a horizontal stretch by a factor of 2, a shift right 5 units, and a shift up 4 units.
h(x) = -3 [√0.5(x-5)] + 4
500
Given the parent function of f(x) = 1/x, write the equation of the transformed function and describe the transformations in order that occur to the transformed function:
g(x) = -f[-2(x - 0.5)] + 1
g(x) = -[-1/[2(x-0.5)]] + 1
g(x) = 1/[2(x-0.5)] + 1
1. vertical reflection (over the x-axis)
2. horizontal reflection (over the y-axis)
3. horizontal compression by a factor of 1/2
4. shift right 0.5 units
5. shift up 1 unit