Inductive Patterns
Logic Statements
Direct and Indirect Proof
Euler Diagrams
Misc Math
100
Find the next two terms in the pattern
2, 5, 8, 11...
14, 17
100
Finish the statement.
All dogs like fetch. Spot is a dog. Therefore...
Spot likes fetch.
100
True or False:
To prove something in mathematics, you must make a convincing argument but it is okay if there are small flaws in the argument.
False. A proof must use logic and reason to demonstrate with certainty the thing that is being proved.
100
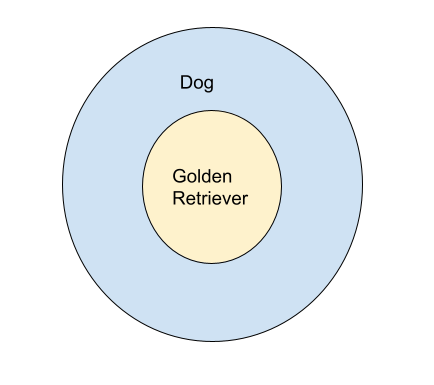
Draw an Euler diagram to represent the following scenario:
If you are a golden retriever, then you are a dog.
100
Solve for 'x'.
12x=6x^2-18
x=3, x=-1
200
Find the next two terms in the pattern
2, 3, 5, 8, 12, 17...
23, 30
200
True or false:
p->q
q
therefore p
False. It is ambiguous.
200
What is the first step of indirect proof by contradiction?
Temporarily assume the opposite (negation) of what you are trying to prove.
200
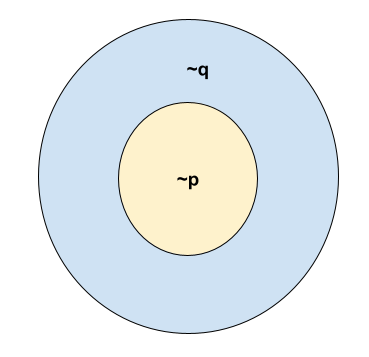
Draw an Euler diagram to represent the following conditional statement:
~p->~q
200
The area of a square is 64cm2. What is its perimeter?
32 cm
300
Find the next two terms in the sequence
2, 5, 10, 13, 26, 29...
58, 61
300
Is the conclusion reached valid?
I go to the gym on Mondays. Today is Wednesday. Therefore I do not go to the gym.
Invalid conclusion.
If it is Monday then I go to the gym. Can still go to the gym other days (ambiguous).
300
Prove that x!=5 if
-2x+10!=0
Temporarily assume x=5, substitute into the equation, simplify and demonstrate that it makes the equation false, thus a contradiction.
300
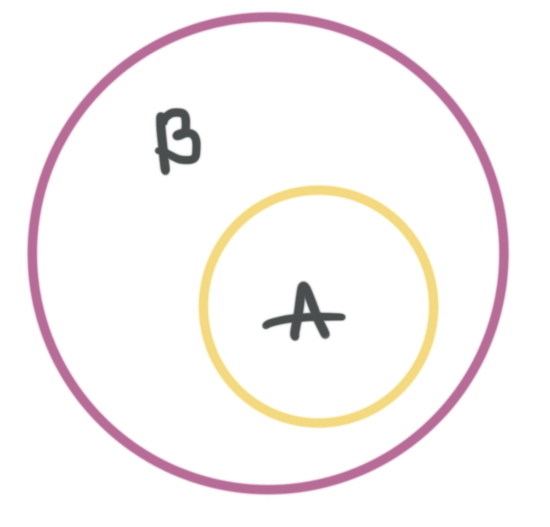
Based on the Euler Diagram, is it possible that the
biconditional statement A<-->B is true? Explain why or why not.
No because the statement B-->A is not true, B can be true while A is not true.
300
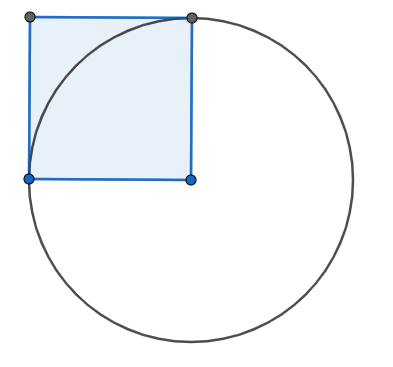
The area of the square is 121m2. What is the circumference of the circle? (leave answer in terms of pi)
22pi m^2
400
5, 2, -6, -9, 27, 24, -72...
-75, 225
400
Determine if the conclusion reached is valid.
~p->q
~q
therefore p
True, this is a valid conclusion (law of contrapositives)
400
Prove that the sum of two odd numbers is always even.
Work through the proof to ultimately demonstrate the sum of two odd numbers can be represented as 2(j + k + 1) which must be even as this is a multiple of 2.
400
Write 6 valid conditional statements that stem from this diagram
C->A
C->B
A->B
~A->~C
~B->~A
~B->~C
400
What are the last two digits of the number represented by the following expression:
2021^2022
41