Geometric
Arithmetic
Either
What is the formula?
100
Beth runs a lap in 2 minutes. Every month she trains She gets 16% faster. How fast was her lap time after 5 months?
59.745 seconds
100
Kevin wants to run a marathon. He starts training by running 1 and a half miles every day for a week. The next week he ran half a mile more than the week before, for every day the second week. If every week he increased his distance by a half mile how many weeks will in take him to run a marathon? (note we assume a marathon is exactly 26 miles.
50 weeks
100
This sequence series results in the addition of CONSECUTIVE numbers. 1 + 2 + 3 + 4 + ...
At what address will the sum equal 1,000,000?
approx 1413.71
100
Un=U1+(n-1)d
Arithmetic Sequence
200
Dak is a quarterback. His first game this season he threw for 202 yards. Every game after he threw 5% more yards. After a 16 game season (since the cowboys wont make the playoffs) how many yards will Dak of thrown total?
4778.81 yards
200
Sergei is training to be a weightlifter. Each day he trains at the local gym by lifting a metal bar that has heavy weights attached. He carries out successive lifts. After each lift, the same amount of weight is added to the bar to increase the weight to be lifted.
Sergei’s friend, Yuri, records the weight of each lift. Unfortunately, last Monday, Yuri misplaced all but two of the recordings of Sergei’s lifts.
On that day, Sergei lifted 21 kg on the third lift and 46 kg on the eighth lift.
For that day find how much weight was added after each lift?
5kg
200
If I had one grain of rice and I doubled it every day for 31 days how much rice will I have by the thirty first?
1,073,741,824 grains
200
Un=U1(r)^(n-1)
Geometric sequence
300
A factory in 1909 is producing candy. It makes 2000 pounds per quarter. However as the decades pass its efficiency improves by 321% per decade. What year is it when 337,436,388 pounds is produced in a quarter.
2019
300
The first term of an arithmetic sequence is 0 and the common difference is 12.
Find the value of the 96th term of the sequence.
1140
300
The table shows the first five terms of three sequences: u , v and w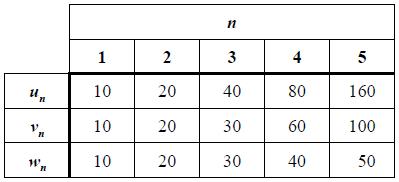 
State which is not a Arithmetic or a Geometric sequence
V
300
Sn=n/2(2U1+(n-1)d) or Sn=n/2(U1+Un)
Arithmetic Series
400
The first term of a geometric sequence is 2 and the third term is 2.205.
Calculate the common ratio of the sequence;
r = 1.05
400
The company Snakezen’s Ladders makes ladders of different lengths. All the ladders that the company makes have the same design such that:
the first rung is 30 cm from the base of the ladder,
the second rung is 57 cm from the base of the ladder,
the distance between the first and second rung is equal to the distance between all adjacent rungs on the ladder.
Find the distance from the base of this ladder to the top rung.
300cm
400
The table shows the first five terms of three sequences: u , v and w
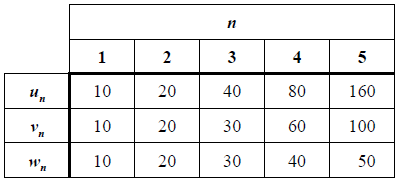
Find the exact value of the 11th term of the geometric sequence.
10240
400
Sn=((U1(r^n-1))/(r-1)) or Sn=((U1(1-r^n))/(1-r))
Geometric Series
500
Matryoshka dolls, or Russian dolls, are similarly designed dolls which open up and fit inside each other.
The largest set of these type of dolls is a 51 piece set which was completed in 2003. The height of the largest piece in this set is 54 cm. The heights of successive smaller dolls are 94 %.
Find the total height if all 51 dolls were placed one on top of another.
862 cm
500
The table shows the first five terms of three sequences: u , v and w.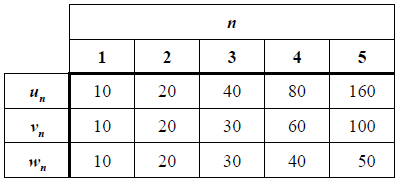 
Find the sum of the first 20 terms of the arithmetic sequence.
2100
500
Matryoshka dolls, or Russian dolls, are similarly designed dolls which open up and fit inside each other.
The largest set of these type of dolls is a 51 piece set which was completed in 2003. The height of the largest piece in this set is 54 cm. The heights of successive smaller dolls are 94 %.
Find the height of the smallest doll in this set.
2.45 (cm)
500
S(infty)=(U1)/(1-r)
Sum of a infinite geometric series