Angle Pairs and Relationships
Triangles and Polygons
Circles and Composite Figures
Coordinate Plane - Basics
Coordinate Plane - Formulas
100
What is the complement of 74.4 degrees?
90 - 74.4 = 15.6 degrees
100
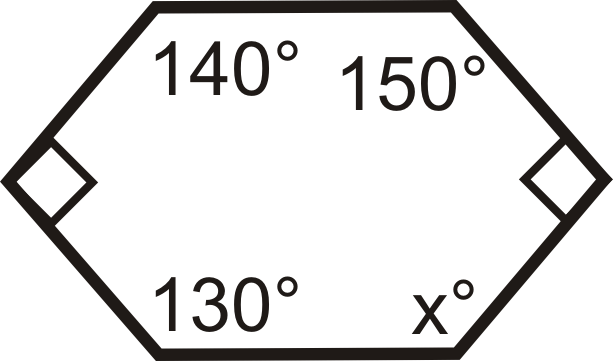
If a polygon has n sides, what is the angle sum of the interior angles of the polygon?
Angle Sum = 180(n-2)
100
A. What is the line segment that goes from the center to the outside of the circle called?
B. What is the line segment that goes through the center and stops at either end of a circle called?
A. Radius
B. Diameter
100
Identify the four quadrants of the coordinate plane below (Use correct Roman Numerals)
100
Find the midpoint of the points (2,4) and (14,0).
Midpoint = (8,2)
200
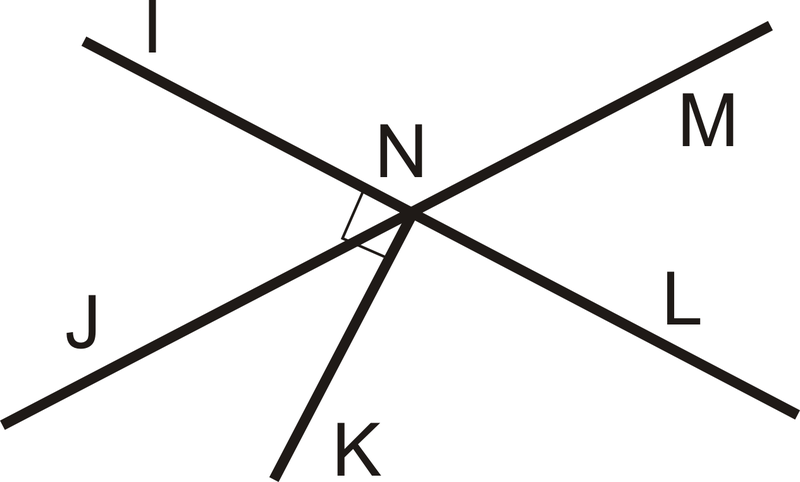
Name a pair of vertical angles and a pair of complementary angles in the diagram above.
Vertical: Angle INJ and Angle MNL (there are others)
Complimentary: Angle INJ and Angle JNK
200
Find the missing angle measure in the triangle below:
180 - 90 - 51 = 39 degrees
200
What is the circumference of a circle with radius 5 meters? (Leave your answer in terms of pi and use correct units).
Circumference = 10pi meters
200
What quadrant is the point (65,-4.5) in?
Quadrant IV
200
Find the distance between the points (5,2) and (8,-2).
Distance = 5
300
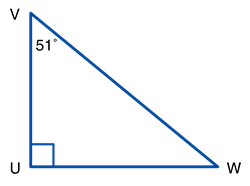
Find the value of x in the diagram:
Set up and solve 9x+72 = 4x+112 (since vertical angles equal each other.
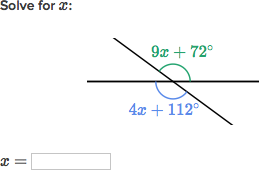
Get x = 8
300
Find the missing angles a and b in the diagram below:
b = 60 degrees
a = 50 degrees
300
Find the area of the green shaded region (exact area or rounded to the nearest hundredth):
Green Area = pi(12)^2 - pi(7)^2
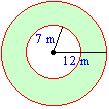
= 144pi - 49pi
= 95pi square meters
= 298.45 square meters
300
What are the coordinates of the points A and D?
A = (1,0)
B = (-3, -5)
300
Find the length of the line segment pictured below as a simplified radical:
Answer: 2sqrt(10)
*Other answers you may have gotten: sqrt(40) isn't simplified, and 6.32 is a rounded approximation (not a radical).
400
Find the value of x and y:
x = 50
y = 40
Solution: Note the angle that is vertical to 130 degrees.
Solve 130 = y+90. Get y=40.
Then, note x and y are complementary.
Solve x+40=90. Get x = 50
400
Find the missing interior angle x (in degrees). Note: Figure not drawn to scale.
Since a hexagon has an interior angle sum of 180(6-2) = 720 degrees, then
130 + 90 + 140 + 150 + 90 + x = 720
So x = 120 degrees
400
Find the perimeter of the composite shape below (exact answer or rounded to the nearest hundredth):
Perimeter = 30 + 30 + 20 + (.5)2pi(10)
= 10pi + 80 mm
(approximately 111.42 mm)
400
Tell me 4 points (i.e. ordered pairs) on the coordinate plane that form the corners of a square.
Infinitely many answers.
One possibility: (0,0), (0,1), (1,0), (1,1)
400
B. (2.1, -14.7)
You can either use the midpoint formula (harder), or plot the points and estimate your answer based on the choices (easier).
500
Angles A and B are supplementary.
If angle A = 11x + 15 and angle B = 3(x-1), find the exact degree measure of each angle.
Set up and solve 11x+15+3x-3=180 for x
Get x = 12
Angle A = 147 degrees
Angle B = 33 degrees
500
Find the missing angles a, b, c and d.
d = 25 degrees
c = 65 degrees
b = 65 degrees
a = 85 degrees
500
Find the area of the entire composite region, measured in square units. Give both the exact answer and a rounded answer to the nearest hundredth.
Exact Area = 192 + 192 + 96 + pi(10)^2
= 100pi + 480 square units
which is approximately 794.16 square units
500
Name three ordered pairs in the second quadrant that lie on a straight line that isn't vertical nor horizontal.
Infinitely many answers.
One possibility: (-1,1), (-2,2), (-3,3)
500
Find the exact area of the composite figure below (i.e. do not round your answer). Use correct units (assume the x and y axes are measured in inches):
Exact Area = 36 + 8pi square units (which is approximately 61.13 square units).