What is up 7 and left 12 in proper translation rule notation?
Example: (x +/- __, y +/- __)
(x - 12, y + 7)
If point A is located at (5,6) and it is reflected across the x-axis, what would the coordinate of A' be?
(5,-6)
A rotation results in a congruent figure. True or False?
True
Find the scale factor.
k = 2
Given the translation rule (x - 5, y + 4), how do we move our coordinates?
All coordinates move left 5 and up 4
What sequence of transformations maps Figure A to Figure A"?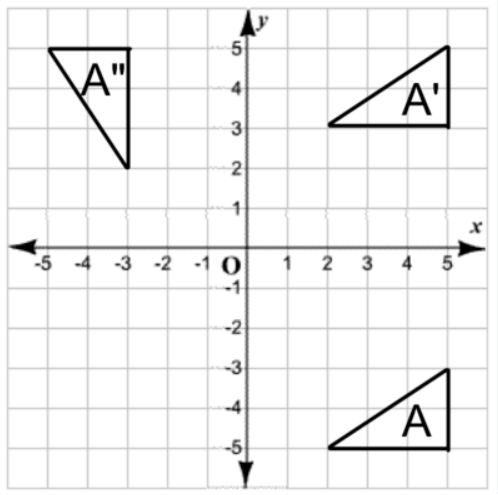
Translate up 8 units, then rotate 90 degrees CCW about the origin
What is the translation rule that maps Triangle PQR to Triangle P'Q'R'?
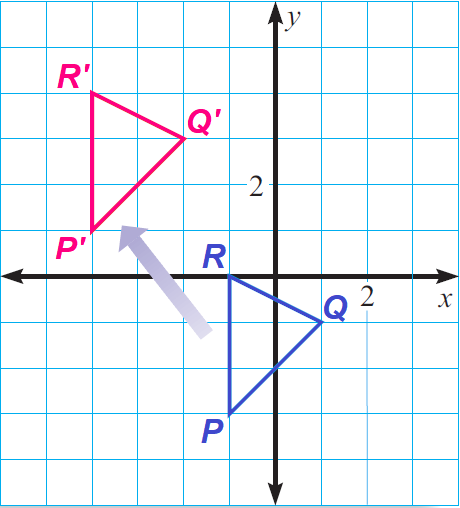
(x, y) --> (x - 3, y + 4)
If your pre-image figure is in quadrant III and you reflect it across the y axis, what quadrant would your image be in?
Quadrant IV
If you pre-image is located in Quadrant II and you rotate it counter-clockwise 90 degrees, what quadrant would your image be located in?
Quadrant III
When dilating a figure by a scale factor between 0 and 1, this happens.
A reduction in size (it shrinks/becomes smaller)
When reflecting a coordinate across the x-axis, the x-values stay the same and this happens to the y-values...
The sign changes
If the following figure is translated down 2 units, and then reflected across the x-axis, where will B'' be?
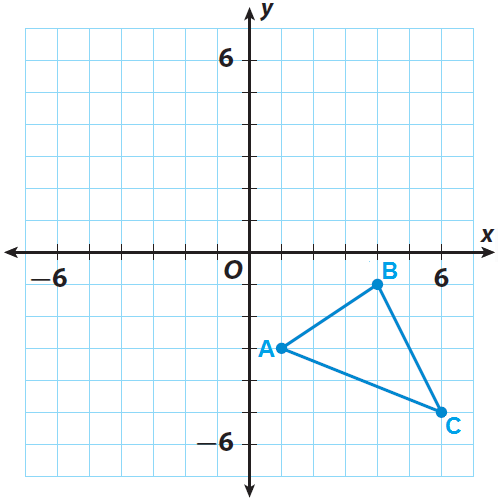
B"(4, 3)
If point A is at (2,2) and you translate it left 5 units, what would the point at A' be?
(-3,2)
If point K is located at (-2,-4) and it is reflected across the y-axis, what is the coordinate of K'?
(2,-4)
How many degrees counter-clockwise did Triangle BCD rotate?
90 degrees
Triangle XYZ consists of vertices X(2, 2), Y(10, -4), and Z(0, 8). Find the coordinates of Triangle X'Y'Z' after a dilation of 2 centered around the origin.
X'(4, 4), Y'(20, -8), Z'(0, 16)
If L (-2, 9) is rotated 180 degrees about the origin, where will L' be located?
L' (2, -9)
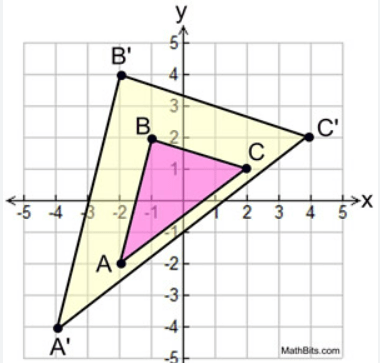
What sequence of transformations maps Triangle ABC to A"B"C"?
translation (x,y) --> (x-1, y-5) followed by reflection over the y-axis
If point J is at (3,-4) and you translate it left 5 units & up 7 units, what would be the coordinate of J'?
(-2,3)
If a figure begins in Quadrant III, is reflected across the x-axis, and then is reflected a second time across the y-axis, which quadrant will it be located in now?
Quadrant I
If you have point G at (-3,2) and you rotate it 180 degrees, what would the point G' be?
(3, -2)
If triangle XYZ has vertices X(10, 6), Y(8, -8) and Z(12, -4) and is dilated by a scale factor of 9, what are the coordinates of the vertices of X'Y'Z'?
X'(90, 54)
Y'(72, -72)
Z'(108, -36)
Which transformation does NOT result in a congruent figure?
Dilations
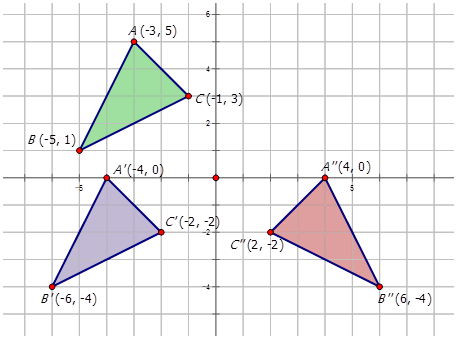
What composite transformation maps ∆ABC onto ∆A''B''C''?
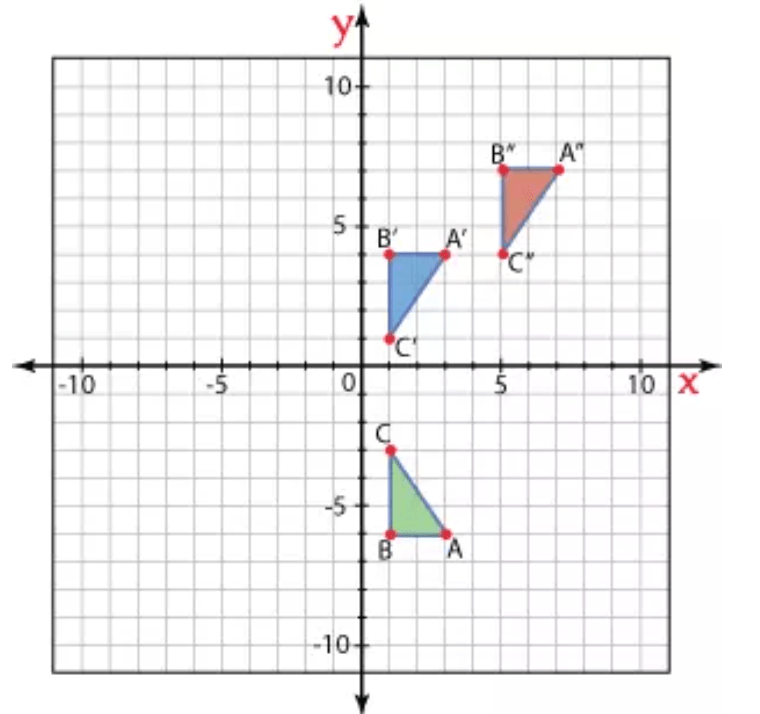
Reflection across y=-1, then translation (x,y) --> (x+4, y+3)
If point W is at (-5,0) and first you translate it right 7 units & up 3 units, then you translate it left 2 units & down 3 units, what would the point at W" be?
(0,0)
If Z (2, 2) is reflected across the x-axis, and then again over the y-axis, what is the coordinate of Z" following the double reflection?
Z"(-2, -2)
The coordinate C (9, -10) is rotated 270 degrees counter-clockwise. What is the coordinate of C'?
C'(-10, -9)
Find the coordinate for Point X (10, -15) after a dilation of 4/5 centered around the origin.
X' (8, -12)
If vertex L starts at (5, 6) and is first rotated 90 degrees clockwise, and then is reflected across the y-axis, what will be the coordinate of L"?
L(5, 6) --> L'(6, -5) --> L"(-6, -5)
A composite transformation of two reflections over the x and y axes is equivalent to what single transformation?
Rotation 180 degrees about the origin